《带电粒子场中动　考题类型须弄清》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

带电粒子场中动　考题类型须弄清

范文

华兴恒

带电粒子在不同的场中运动是高考的热点，有些同学对此类问题望而生畏，常常不知如何入手求解，导致考场失利。为此下面对此类考题分类例析，只要大家分类掌握的了这些题型的解法，然后达到举一反三，便可触类旁通，为高考打下坚实的基础.

一、带电粒子在电场中的运动问题

【例1】（2016·全国卷Ⅱ）如图1所示，P是固定的点电荷，虚线是以P为圆心的两个圆. 带电粒子Q在P的电场中运动，运动轨迹与两圆在同一平面内，a、b、c为轨迹上的三个点. 若Q仅受P的电场力作用，其在a、b、c点的加速度大小分别为aa、ab、ac，速度大小分别为va、vb、vc. 则（ ??）

A. aa > ab > ac，va > vc > vb

B. aa > ab > ac，vb > vc > va

C. ab > ac > aa，vb > vc > va

D. ab > ac > aa，va > vc > vb

解析：因为带电粒子只受电场力的作用，由点电荷电场强度公式E =k■可知，离场源点电荷P越近，电场强度越大，Q受到的电场力也就越大，则由牛顿第二定律可知，加速度越大，故有ab > ac > aa，则选项A、B错误;由力与运动的关系可知，Q受到的库仑力指向运动轨迹凹的一侧，因此Q与P带同种电荷，Q从c到b的过程中，电场力做负功，动能减少，从b到a的过程中，电场力做正功，动能增加，因此Q在b点的速度最小，由于b、c两点的电势差的绝对值小于a、b两点的电势差的绝对值，因此Q从c到b的过程中，动能的减少量小于从b到a的过程中动能的增加量，Q在c点的动能小于在a点的动能，即有va > vc > vb. 故应选D.

点评：掌握点电荷电场的特点，明确电场力做功与电势差的关系，是顺利求解本题的关键. 熟知带电粒子仅在电场力的作用下，其加速度的大小取决于场强的大小，其速度的大小取决于电场力做功的正负与大小. 要注意的是：带电粒子在电场中运动时，若只受电场力的作用，则带电粒子的动能与其势能的总和为一定值.

【例2】（2016·北京卷）如图2所示，电子由静止开始经加速电场加速后，沿平行于板面的方向射入偏转电场，并从另一侧射出. 已知电子质量为m，电荷量为e，加速电场电压为U0，偏转电场可看作匀强电场，极板间电压为U，极板长度为L，板间距离为d.

（1）忽略电子所受重力，求电子射入偏转电场时的初速度v0和从电场射出时沿垂直板面方向的偏转距离△y.

（2）分析物理量的数量级是解决物理问题的常用方法. 在解决（1）问忽略了电子所受的重力，请利用下列数据分析说明其原因. 已知U = 2.0 × 102 V，d = 4.0 × 10-2m，m = 9.1 × 10-31 kg，e = 1.6 × 10-19 C，g = 10 m/s2.

（3）极板间既有静电场也有重力场. 电势反映了静电场各点的能的性质，请写出电势φ的定义式. 类比电势的定义方法，在重力场中建立“重力势”φG的概念，并简要说明电势和“重力势”的共同特点.

解析：该题主要考查带电粒子在加速电场和偏转电场中的運动、电势的定义等知识.

（1）根据功和能的关系，有eU0 =■mv20，则电子射入偏转电场的初速度v0 =■.

在偏转电场中电子的运动时间为△t =■= L■，可得偏转距离△y =■（a△t）2 =■·■（△t）2 =■.

（2）考虑电子所受重力和电场力的数量级，有重力G = mg≈10-29 N，电场力F =■≈10-15 N. 因为F >> G，因此无须考虑电子所受的重力作用.

（3）电场中某点电势φ定义为电荷在该点的电势能EP与其电荷量q的比值，即φ =■. 由于重力做功与路径无关，可以类比静电场电势的定义，将重力场中物体在某点的重力势能EG与其质量m的比值叫做“重力势”，即φG =■. 电势φ和重力势φG都是反映场的能的性质的物理量，仅由场本身的因素决定.

【例3】（2015·全国卷Ⅱ）如图3所示，一质量为m、电荷量为q（q > 0）的粒子在匀强电场中运动，A、B为其运动轨迹上的两点. 已知该粒子在A点的速度大小为v0，方向与电场方向的夹角为60°，它运动到B点时速度方向与电场方向的夹角为30°，不计重力. 求A、B两点间的电势差.

解析：设带电粒子在B点的速度大小为vB，粒子在垂直于电场方向的速度分量不变，即vBsin30° = v0sin60°，由此可得vB =■v0.

设A、B两点间的电势差为UAB，则由动能定理有

qUAB =■m（v2B-v20），将vB代入可解得UAB =■.

点评：带电粒子在匀强电场中运动，垂直电场方向上其分速度大小不变，电场力只改变带电粒子沿电场方向上的分速度，两个方向上分速度的大小关系也就决定了带电粒子运动方向与电场线方向的夹角，重点是将速度分解，然后根据qU =△Ek即可获解.

二、带电粒子在磁场中的运动问题

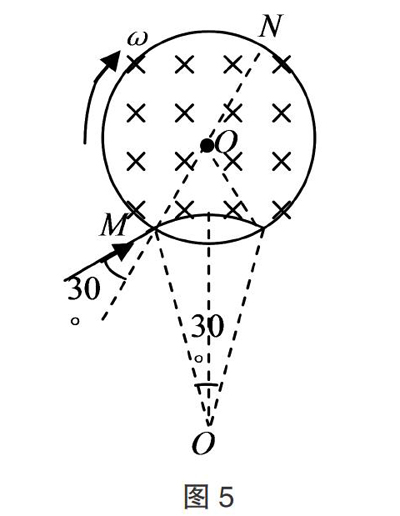
【例4】（2016·全国卷Ⅱ）一圆筒处于磁感应强度大小为B的匀强磁场中，磁场方向与筒的轴平行，筒的横截面如图4所示. 图中直径MN的两端分别开有小孔，筒绕其中心轴角速度ω顺时针转动. 在该截面内，一带电粒子从小孔M射入圆筒，射入时的运动方向与MN成30°角. 当圆筒转过90°时，该粒子恰好从小孔N飞出圆筒. 不计重力，若粒子在筒内未与筒壁发生碰撞，则带电粒子的比荷为（ ???）

A. ■ B. ■ C. ■ D. ■

解析：由题意可知带电粒子在磁场中做圆周运动的轨迹如图5所示. 由几何关系可知，带电粒子在磁场中做圆周运动的圆弧所对的圆心角为30°，因此带电粒子在磁场中运动的时间为t =■×■;由题意可知，带电粒子在磁场中运动的时间与筒转过90°所用的时间相等，即■=■×■，求得■=■. 故应选A.

点评：求解本题的关键是要能够正确的审题，并能够根据审题结果正确地画出粒子运动的轨迹，并找准几何关系. 简单地说就是：定圆心，画轨迹，由几何知识求半径，找圆心角求时间. 否则会导致错解的发生.

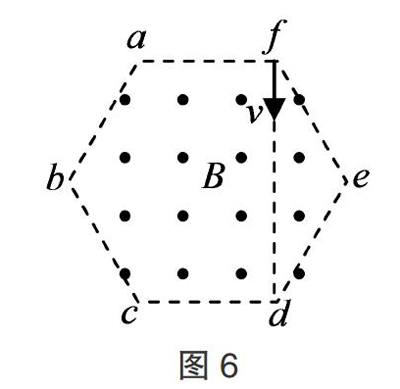
【例5】（2016·四川卷）如图6所示，正六边形abcdef区域内有垂直纸面的匀强磁场. 一带正电的粒子从f点沿fd方向射入匀强磁场区域，当速度大小为vb时，从b点离开磁场，在磁场中运动的时间为tb;当速度大小为vc时，从c点离开磁场，在磁场中运动的时间为tc. 不计粒子重力，则（ ???）

A. vb ∶ vc = 1 ∶ 2， tb ∶ tc = 2 ∶ 1

B. vb ∶ vc = 2 ∶ 1， tb ∶ tc = 1 ∶ 2

C. vb ∶ vc = 2 ∶ 1， tb ∶ tc = 2 ∶ 1

D. vb ∶ vc = 1 ∶ 2， tb ∶ tc = 1 ∶ 2

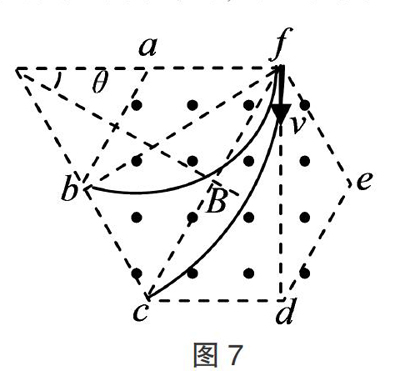
解析：设正六边形的边长为l，一带正电的粒子从f沿fd方向射入磁场区域，当速度大小为vb时，从b点离开磁场，则由几何关系可知粒子在磁场中做圆周运动的半径为rb = l，粒子在磁场中做圆周运动的轨迹所对的圆心角为120°. 因为由洛伦兹力提供向心力，则有Bqvb =■，解得l =■，且T =■，可得tb =■·■;当速度大小为vc时，从c点离开磁场，则有几何关系可知，粒子在磁场中做圆周运动的半径rc = l +■= 2l，同理有2l = ■，tc =■·■. 解得vb ∶ vc = 1 ∶ 2， tb ∶ tc = 2 ∶ 1，则选项A正确. 故应选A.

点评：解答本题的关键是要确定粒子做圆周运动的圆心，然后根据几何关系求出粒子做圆周运动的半径以及运动轨迹所對应的圆心角，这样就能够顺利获解.

【例6】（2016·全国卷Ⅲ）平面OM和平面ON之间的夹角为30°，其横截面（纸面）如图8所示，平面OM上方存在匀强磁场，磁感应强度大小为B，方向垂直于纸面向外. 一带电粒子的质量为m，电荷量为q（q > 0）. 粒子沿纸面以大小为v的速度从OM的某点向左上方射入磁场，速度与OM成30°角. 已知该粒子在磁场中的运动轨迹与ON只有一个交点，并从OM上另一点射出磁场. 不计重力，粒子离开磁场的出射点到两平面交线O的距离为（ ???）

A. ■B. ■C. ■D. ■

解析：如图9所示为粒子在匀强磁场中的运动轨迹示意图，设出射点为P，粒子运动轨迹与ON的交点为Q，粒子入射方向与OM成30°角，则射出磁场时速度方向与MO成30°角，由几何关系可知，PQ⊥ON，故出射点到O点的距离为轨道圆直径的2倍，即4R. 又粒子在匀强磁场中运动的轨迹半径R =■，故应选D.

点评：准确作出带电粒子在磁场中的运动轨迹是解题的关键，在做题时可以运用直尺和圆规或小硬币辅助作图，以利于顺利求解.

【例7】（2013·课标全国卷I）如图10所示，半径是R的圆是一圆柱形匀强磁场区域的横截面（纸面），磁感应强度大小为B，方向垂直于纸面向外. 一电荷量为q（q > 0）、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为■. 已知粒子射出磁场与射入磁场时运动方向间的夹角为60°，则粒子的速率为（不计重力）

A. ■B. ■C. ■D. ■

解析：作出粒子运动轨迹如图11中实线所示. 因P到ab的距离为■，可知α = 30°. 因粒子速度方向改变60°，可知转过的圆心角2θ = 60°. 由图中几何关系有（r +■）tanθ = Rcosα，解得r = R. 再由Bqv = m■，可得v =■. 则选项A、C、D错误，选项B正确. 故应选B.

点评：正确地描绘粒子运动轨迹是顺利求解本题的关键，然后根据几何关系，利用边、角关系确定圆的半径，进而根据圆周运动的规律便可简捷地求出粒子的速率.

【例8】（2018·江苏卷）如图12所示，真空中四个相同的矩形匀强磁场区域，高为4d，宽为d，中间两个磁场区域间隔为2d，中轴线与磁场区域两侧相交于O、O′点，各区域磁感应强度大小相等. 某粒子质量为m、电荷量为 + q，从O沿轴线射入磁场. 当入射速度为v0时，粒子从O上方■处射入磁场. 取sin53°= 0.8，cos53°= 0.6.

（1）求磁感应强度B的大小;

（2）入射速度为5v0时，求粒子从O运动到O′的时间t;

（3）入射速度仍为5v0，通过沿轴线OO′平移中间两个磁场（磁场不重叠），可使粒子从O运动到O′的时间增加△t，求△t的最大值.

解析：（1）粒子圆周运动的半径r0 =■，由题意知r0 =■，解得B =■.

（2）设粒子在矩形磁场中的偏转角为α，则由d = rsinα，得sinα =■，即α = 53°.

在一个矩形磁场中的运动时间t1 =■=■，解得t1 =■，直线运动的时间t2 =■，解得t2 =■，则4t1 + t2 =（■）■.

（3）将中间两磁场分别向中央移动距离x，则粒子向上的偏移量y = 2r（1-cosα）+ xtanα. 由y ≤ 2d，解得x ≤■d，则当xm =■d时，△t有最大值.

粒子直线运动路程的最大值sm =■+（2d - 2xm）= 3d，增加路程的最大值△sm = sm - 2m = d，则增加时间的最大值△tm =■=■.

點评：这道题是压轴题，将磁学知识与力学知识有机地结合在一起，目的在于考查大家综合运用所学知识解决实际问题的能力.

三、带电粒子在组合场中的运动问题

【例9】（2017·全国卷Ⅰ）如图13，空间某区域存在匀强电场和匀强磁场，电场方向竖直向上（与纸面平行），磁场方向垂直于纸面向里. 三个带正电的微粒a、b、c电荷量相等，质量分别为ma、mb、mc. 已知在该区域内，a在纸面内做匀速圆周运动，b在纸面内向右做匀速直线运动，c在纸面内向左做匀速直线运动. 下列选项正确的是（ ???）

A. ma > mb > mc B. mb > ma > mc

C. mc > ma > mb D. mc > mb > ma

解析：a在纸面内做匀速直线运动，可知在竖直方向上，a的重力与所受电场力平衡，洛伦兹力提供其做匀速圆周运动的向心力，则有ma g = qE;b在纸面内向右做匀速直线运动，根据左手定则，可知其所受的洛伦兹力方向竖直向上，由力的平衡条件有mb g = qE + F洛;c在纸面内向左做匀速直线运动，根据左手定则，可知其所受洛伦兹力方向向下，由力的平衡条件有mc g = qE - F洛. 因为三个微粒所带的电荷量相等，所以mb g > ma g > mc g，即mb > ma > mc. 故应选B.

点评：（1）在对三个微粒进行受力分析时，注意不能遗漏重力;（2）注意b、c微粒的速度方向相反，它们所受的洛伦兹力的方向也相反. 此外，在判断微粒所受洛伦兹力的方向时务必要记住是用左手.

【例10】（2018·北京）某空间存在匀强磁场和匀强电场. 一个带电粒子（不计重力）以一定的初速度射入该空间后，做匀速直线运动;若仅撤除电场，则该粒子做匀速圆周运动. 下列因素与完成上述两类运动无关的是（ ???）

A. 磁场和电场的方向 B. 磁场和电场的强弱

C. 粒子的电性和电量 D. 粒子入射时的速度

模型分析：由qvB = qE可知，带电粒子只要满足v =■，就能通过“速度选择器”. 因此与粒子的电性和电量无关.

解析：在匀强磁场和匀强电场的叠加区域中，一个带电粒子射入后做匀速直线运动，则它所受的洛伦兹力和电场力大小相等、方向相反，即qvB = qE，故v =■，因此粒子的运动，与粒子的电性和电量均无关. 故应选C.

点评：本题主要考查带电粒子在匀强磁场和匀强电场的叠加场中的运动问题，目的在于考查同学们灵活运用所学知识解决问题的能力.

【例11】（2016·北京卷）如图14所示，质量为m、电荷量为q的带电粒子，以初速度v沿垂直磁场方向射入磁感应强度为B的匀强磁场，在磁场中做匀速圆周运动. 不计带电粒子所受的重力.

（1）求粒子做匀速圆周运动的半径R和周期T;

（2）为使该粒子做匀速直线运动，还需要同时存在一个与磁场方向垂直的匀强电场，求电场强度E的大小.

解析：（1）因洛伦兹力提供向心力，则有f = qvB = m■，据此可求得带电粒子做匀速圆周运动的半径R =■，匀速圆周运动的周期T =■=■.

（2）带电粒子所受的电场力为F = qE，洛伦兹力为f = qvB. 因带电粒子做匀速直线运动，则有qE = qvB，据此可得电场强度的大小为E = vB.

【例12】（2016·天津卷）如图15所示，空间中存在着水平向右的匀强电场，电场强度大小为E = 5■N/C，同时存在着水平方向的匀强磁场，其方向与电场方向垂直，磁感应强度大小B = 0.5 T. 有一带正电的小球，质量m = 1 × 10-6 kg，电荷量q = 2 × 10-6 C，正以速度v在图示的竖直平面内做匀速直线运动，当经过P点时撤掉磁场（不考虑磁场消失引起的电磁感应现象），取g = 10 m/s2. 求：

（1）小球做匀速直线运动的速度v的大小和方向;

（2）从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t.

解析：（1）小球匀速直线运动时受力情况如图16所示，其所受的三个力在同一平面内，合力为零，则有qvB =■，代入已知数据可解得v = 20 m/s.

速度的方向斜向右上方，与电场E的方向之间的夹角θ满足tanθ =■，代入已知数据可解得tanθ =■，则θ = 60°.

（2）方法1：撤去磁场，小球在重力与电场力的合力作用下做类平抛运动，设其加速度为a，则有a =■……①

设撤掉磁场后小球在初速度方向上的分位移为x，则有x = vt……②

设小球在重力与电场力的合力方向上分位移为y，则有y =■at2……③

a与mg的夹角与v和E的夹角相同，均为θ，又tanθ =■……④

联立以上四式并将θ = 60°代入可解得t = 2■s ≈ 3.5 s.

方法2：撤去磁场后，由于电场力垂直于竖直方向，它对竖直方向的分运动没有影响，以P点为坐标原点，竖直向上为正方向，小球在竖直方向上做匀减速运动，其初速度为vy = vsinθ;若使小球再次经过P点所在的电场线，仅需小球的竖直方向分位移为零，则有vyt -■gt2 = 0. 由以上两式并将θ = 60°代入可解得t = 2■s ≈ 3.5 s.

点评：由于带电小球在复合场中运动受到重力、电场力、洛伦兹力的作用，洛伦兹力方向与速度方向垂直，且大小与速度成正比，所以凡是带电小球在复合场中做直线运动，则必为匀速直线运动. 据此可利用平衡条件列出相关方程快速求解.

【例13】（2018·全国卷Ⅱ）一足够长的条状区域内存在匀强电场和匀强磁场，其在xOy平面内的截面如图17所示：中间是磁场区域，其邊界与y轴垂直，宽度为l，磁感应强度的大小为B，方向垂直于xOy平面;磁场的上、下两侧为电场区域，宽度为l′，电场强度的大小均为E，方向均沿x轴正方向;M， N为条状区域边界上的两点，它们的连线与y轴平行. 一带正电的粒子以某一速度从M点沿y轴正方向射入电场，经过一段时间后恰好以从M点入射的速度从N点沿y轴正方向射出. 不计重力.

（1）定性画出该粒子在电磁场中运动的轨迹;

（2）求该粒子从M点射入时的速度的大小;

（3）若该粒子进入磁场时的速度方向恰好与x轴正方向的夹角为■，求该粒子的比荷及其从M点运动到N点的时间.

解析：（1）粒子运动的轨迹如图18所示.（粒子在电场中的轨迹为抛物线，在磁场中为圆弧，上下对称）

（2）粒子从电场下边界入射后在电场中做类平抛运动. 设粒子从M点射入时速度的大小为v0，在下侧电场中运动时间为t，加速度的大小为a;粒子进入磁场的速度沿电场方向的分量为v1. 则根据牛顿第二定律有：qE = ma……①

式中q和m分别为粒子的电荷量和质量.

由运动学公式有：

v1 = at……②

l′= v0 t……③

v1 = vcosθ……④

粒子在磁场中做匀速圆周运动，设其运动轨道半径为R，则由洛伦兹力公式和牛顿第二定律有：

qvB =■……⑤

由几何关系有：l = 2Rcosθ……⑥

联立以上各式可解得：v0 =■……⑦

（3）由运动学公式和题给数据可得：v1 = v0 cos■……⑧

联立①②③⑦⑧可解得：■=■……⑨

设粒子由M点运动到N点所用的时间为t′，则有：

t′= 2t +■T……⑩

式中T是粒子在磁场中做匀速圆周运动的周期：

T =■……？輥？輯？訛

联立③⑦⑨⑩？輥？輯？訛可解得：t′ =■（1+■）.

点评：本题主要考查带电粒子在电磁组合场中的运动，目的是为了考查同学们的综合分析能力和运用数学知识解决物理问题的能力.

四、带电粒子先后在两种不同场中运动的问题

【例14】（2012·课标全国卷）如图19所示，一半径为R的圆表示一柱形区域（纸面）. 在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，离开时速度方向与直线垂直. 圆心O到直线的距离为■R. 现将磁场换为平行于纸面且垂直于直线的匀强磁场，同一粒子以同样速度沿直线在a点射入柱形区域，也在b点离开该区域. 若磁感应强度大小为B，不计重力，求电场强度的大小.

解析：粒子在磁场中做圆周运动，设圆周的半径为r，由牛顿第二定律和洛伦兹力公式得

qvB = m■……①

式中v为粒子在a点的速度.

如图20，过b点和O点作直线的垂线，分别与直线交于c、d两点，则由几何关系可知，线段ac、bc与过a、b两点的轨迹圆弧的两条半径（未画出）围成一正方形. 因此有

ac = bc = r……②

设cd = x，则由几何关系可得

ac =■R + x……③

bc = ■R + ■……④

联立②③④式可解得r =■R……⑤

再考虑粒子在电场中的运动. 设电场强度的大小为E，粒子在电场中做类平抛运动，设其加速度大小为a，则由牛顿第二定律和带电粒子在电场中的受力公式可得

qE = ma……⑥

粒子在电场方向和直线方向所走的距离均为r，则由运动学公式可得

r =■at2……⑦

r = vt……⑧

式中t是粒子在电场中运动的时间.

联立①⑤⑥⑦⑧式可解得E =■.

【例15】（2018·全国I卷）如图21，在y > 0的区域存在方向沿y轴负方向的匀强电场，电场大小为E;在y < 0的区域存在着方向垂直于xOy平面向外的匀强磁场. 一个氕核11H和一个氘核21H先后从y轴上y = h点以相同的动能射出，速度方向沿x轴正方向. 已知11H进入磁场时，速度方向与x轴正方向的夹角为60°，并从坐标原点O处第一次射出磁场. 11H的质量为m，电荷量为q，不计重力. 求：

（1）11H第一次进入磁场的位置到原点O的距离;

（2）磁场的磁感应强度大小;

（3）21H第一次离开磁场的位置到原点O的距离.

分析：（1）根据11H进入磁场时速度方向与x轴正方向的夹角为60°，利用速度的分解与类平抛运动规律得出氕核11H第一次进入磁场的位置到原点的距离. （2）画出氕核11H在匀强磁场中的运动轨迹，利用几何关系得出氕核11H在匀强磁场中运动的轨道半径，运用洛伦兹力提供向心力列方程得出磁场的磁感应强度大小. （3）可画出氘核21H在匀强磁场中的运动轨迹，运用洛伦兹力提供向心力列方程得出氘核21H在匀强磁场中的轨道半径，利用几何关系得出氘核21H第一次离开磁场时的位置到原点O的距离.

解析：（1）11H在电场中做类平抛运动，在磁场中做圆周运动，运动轨迹如图22所示. 设11H在电场中的加速度大小为a1，初速度大小为v1，它在电场中的运动时间为t1，第一次进入磁场的位置到原点O的距离为s1. 则由运动学公式有：

s1 = v1t1

h =■a1t21

由题给条件，11H进入磁场时速度的方向与x轴正方向夹角为θ1 = 60°. 11H进入磁场时速度的y分量的大小为：a1t1 = v1tanθ1

联立以上各式可求得s1 =■h.

（2）11H在电场中运动时，由牛顿第二定律有：qE = ma1

设11H进入磁场时速度的大小为v1′，则由速度合成法则有：v1′ =■

设磁感应强度大小为B，11H在磁场中运动的圆轨道半径为R1，则由洛伦兹力公式和牛顿第二定律有：qv1′B =■

由几何关系可得s1 = 2R1sinθ1

联立以上各式可解得B =■

（3）设21H在电场中沿x轴正方向射出的速度大小为v2，在电场中的加速度大小为a2，则由题给条件可得：

■（2m）v22=■mv21.

由牛顿第二定律有：qE = 2ma2

设第一次射入磁场时的速度大小为v2′，速度的方向与x轴正方向夹角为θ2，入射点到原点的距离为s2，在电场中运动的时间为t2. 则由运动学公式有：

s2 = v2t2

h =■a2 t22

v2′ =■

sinθ2 =■

联立以上各式可解得：s2 = s1， θ2 = θ1， v2′ =■v1′

设21H在磁场中做圆周运动的半径为R2，则由qv1′B =■和s2 = s1， θ2 = θ1， v2′ =■v1′及粒子在匀强磁场中做圆周运动的半径公式可得：R2 =■=■R1.

所以出射点在原点左侧. 设21H进入磁场的入射点到第一次离开磁场的出射点的距离为s2′，由几何关系有：s2′ = 2R2sinθ2

联立qv1′B =■， s1 = 2R1sinθ1， s2 = s1， θ2 = θ1， v2′=■=v1′， R2 =■=■R1和s2′ = 2R2sinθ2几式可得21H第一次离开磁场时的位置到原点O的距离为：s2′ - s2 =■（■-1）h.

点评：本题重点在于考查带电粒子在电场中的类平抛运动、在匀强磁场中的匀速圆周运动及相关的知识点，目的是为了考查同学们灵活运用相关知识解决实际问题的能力.

【例16】（2018·全国卷Ⅲ）如图23所示，从离子源产生的甲、乙两种离子，由静止经加速电压U加速后在纸面内水平向右运动，自M点垂直于磁场边界射入匀强磁场，磁场方向垂直于纸面向里，磁场左边界竖直. 已知甲种离子射入磁场的速度大小为v1，并在磁场边界的N点射出;乙种离子在MN的中点射出;MN长为l. 不计重力影响和离子间的相互作用. 求：

（1）磁场的磁感应强度大小;

（2）甲、乙两种离子的比荷之比.

解析：（1）設甲种离子所带电荷量为q1、质量为m1，在磁场中做匀速圆周运动的半径为R1，磁场的磁感应强度大小为B，则由动能定理有：q1U =■m1v21……①

由洛伦兹力公式和牛顿第二定律：q1v1B = m1■……②

由几何关系知：2R1 = l……③

联立以上三式可解得：B =■

（2）设乙种离子所带电荷量为q2、质量为m2，射入磁场的速度为v2，在磁场中做匀速圆周运动的半径为R2. 同理有：q2U =■m2v22……④

q2v2B = m2■……⑤

由题给条件有：2R2 =■……⑥

联立以上六式可解得甲、乙两种离子的比荷之比为：■ ∶ ■= 1 ∶ 4.

点评：本题考查带电粒子在电场中加速、在匀强磁场中的匀速圆周运动及相关的知识点，目的在于考查同学们灵活运用相关知识解决实际问题的能力.

【例17】（2018·天津卷）如图24所示，在水平线ab的下方有一匀强电场，电场强度为E，方向竖直向下，ab的上方存在着匀强磁场，磁感应强度为B，方向垂直纸面向里. 磁场中有一内、外半径分别为R、■R的半圆环形区域，外圆与ab的交点分别为M、N. 一质量为m、电荷量为q的带负电粒子在电场中P点静止释放，由M进入磁场，从N射出. 不计粒子重力.

（1）求粒子从P到M所用的时间t;

（2）若粒子从与P同一水平线上的点水平射出，同样能由M进入磁场，从N射出. 粒子从M到N的过程中，始终在环形区域中运动，且所用的时间最少，求粒子在Q时速度v0的大小.

解析：（1）设粒子在磁场中运动的速度大小为v，所受洛伦兹力提供向心力，有：

qvB = m■……①

设粒子在电场中运动所受电场力为F，则有：

F = qE……②

设粒子在电场中运动的加速度为a，则根据牛顿第二定律有：

F = ma……③

粒子在电场中做初速度为零的匀加速直线运动，有：

v = at……④

联立以上各式可解得：t =■.

（2）粒子进入匀强磁场后做匀速圆周运动，其周期与速度、半径无关，运动时间只由粒子所通过的圆弧所对的圆心角的大小决定. 故当轨迹与内圆相切时，所用的时间最短.

设粒子在磁场中的运动轨迹半径为r′，则由几何关系可得：

（r′- R）2 +（■R）2 = r′2……⑤

设粒子进入磁场时速度方向与ab的夹角为θ，即圆弧所对圆心角的一半，则由几何关系可知：

tanθ =■……⑥

粒子从Q射出后在电场中做类平抛运动，在电场方向上的分运动和从P释放后的运动情况相同，所以粒子进入磁场时沿竖直方向的速度同样为v. 在垂直于电场方向上的分速度始终等于v0，则由运动的合成与分解可得：

tanθ =■……⑦

联立①⑤⑥⑦可解得：v0 =■.

责任编辑 ??李平安

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。