《初高中数学衔接中学生数学能力的迁移与发展探究》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

初高中数学衔接中学生数学能力的迁移与发展探究

范文

董莲莲

摘要：数学教学工作中，教师要做好知识点的迁移工作，使学生更好地将学习过的知识点应用起来，以其为基础对新知识点展开学习。教师要帮助学生找到知识点间的联系，明晰知识点间的关系，使学生能够有效地掌握并理解将要学习的数学知识。对初高中数学学科教学工作中如何做好知识点的衔接，实现知识点的有效迁移，促进学生长远发展进行简要分析。

关键词：初高中数学;衔接中学生;数学能力

知识点间的联系是教师开展教学工作中，可以进行有效应用的重要知识。通过知识点间的迁移可以使学生更好地理解新知识，可以使学生对新知识学习过程中带有的畏惧心理得到最大程度的降低。在初高中数学衔接中，学生的能力培养应当成为重点教学内容。教师可以利用思维导图对学生进行引导，使学生在学习的过程中实现对知识点更为有效的理解，使学生能够在知识点的迁移过程中实现个人能力的成长。

一、初高中数学衔接现状与原因

（一）课堂内容的安排

初中课堂教学活动中，由于课堂上的知识内容点较少，所以教师需要在课堂教学中做好知识内容的讲授，学生仅需跟进教师的教学步伐即可。但持续到高中阶段以后，知识量激增，学生的学习任务增大，导致学生复习、练习的时间减少，加之各个学科的课业量增大，学生开始的时候有应接不暇之感，导致课堂内容不是很适应。

（二）教材的编排风格

初中数学教学的内容生动性较好，且与学生实际有着紧密联系。但高中数学教学中，增加了有关几何、映射、函数这类抽象性较强的内容，导致学生在学习的时候倍感吃力。

（三）教学方法的侧重

初中阶段涉及的知识内容有限，学习任务比较轻，教师使用常规教学方法开展教学就能有收获，即使教师给学生讲授各类题型，做归纳总结，但各类题型的内容有限，学生仅凭记忆也能完成好各项。但高中阶段题型变化较多，且随着知识量的增加，学生仅凭记忆难以完成预期教学任务，需要通过理解和分析的方法，自己进行解题方法的推断，教师能给学生讲授的内容仅是“引子”，学生需要在教师引入后，进行深入的探究和学习，所以学习的方法上面有较大的变动，若是在教学中依旧使用单一的教学模式，难以达成理想教学效果。所以教学中培养学生的数学能力就显得尤为重要。

二、初高中数学衔接中学生数学能力迁移与发展的探索

（一）对教材内容所要求的数学能力的理解

1.逻辑思维能力是正确解决问题的主要能力

数学这门学科要想学好，良好的数学能力是关键点。其实学生数学逻辑能力需要通过训练才能获得，很少有人天生就具有较好的逻辑能力，其实小学阶段开展的数学教学就有培养学生逻辑思维能力的一项内容，初中阶段虽然没有言明如何培养学生逻辑思维能力，但每次推理的时候，教师都要给出合理的推理依据，且教材中也有关于逻辑的介绍和相关的逻辑内容概述。就以几何相关知识内容为案例开展分析。

其实根据案例能了解到教材中的思维导向内容，需要在循序渐进中才能更好地延伸数学能力。既然初中到高中是一个进阶，如何在每个进阶的时候培养学生的逻辑思维能力呢？首先，教师要让学生熟悉数学语言，由于语言密码对人的思维有着极大的影响。学生在初中阶段对于逻辑、集合相关知识内容没有了解到，所以难以使用连接词做好严谨的数学内容描述，导致学生在严谨性与表达准确性方面受限。其次，以提取教材中的不等式例子进行概述，在数学教学中等式表示的多为等量的关系，不等式则是不等量的关系，两种关系在自然界中是以基本数学关系的形式存在的。学生在初中阶段学习了不等式，在不等式的基础上又学习了一元一次不等式和一元一次不等式组等相关内容，高中阶段则是引入集合的概念进行不等式的结果展示，然后再深入探究不等式的相关内容，并在教学中继续推广，做好教学延伸。如，初中阶段不等式3-x<2x+6的解集使用的是x>-1。待进入到高中阶段后，进行不等式解集的表达则是使用{x|x>-1}，用来表达一类或者一族的内容，这些类、族的内容都可以使用集合概括。使用该表达方式显得更加严谨与科学，且符号化的表达更为简便。其实无论是初中阶段还是高中阶段，在不等式学习的过程中，在存储知识量不足的情况，教材在不同学习阶段安排不同的教学计划，都是依据学生逻辑思维的发展进行科学合理的安排。知识学习是死的，但是能力是活的，所以在课堂教学的时候要通过量的积累变为成质的飞越，这也是教材中对数学能力迁移与发展的潜在要求。学生要在課前做好仔细的预习，养成较好的自主学习意识和习惯，并在严谨性的知识内容罗列中找寻本课的学习重点，在课堂上重点听讲。

2.空间想象能力

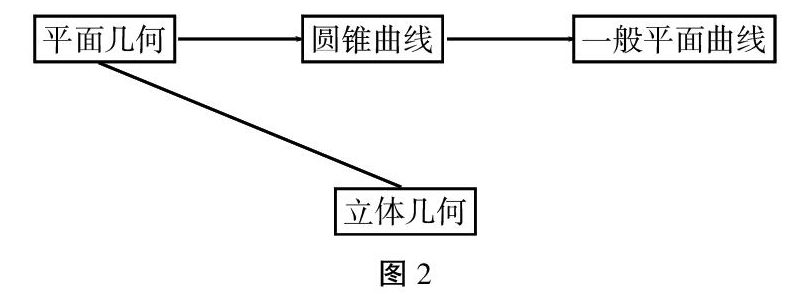
有关空间想象能力的概述无需多说，很多人都对空间想象能力有良好的认知度，但如何在数学学习中不断地诱发学生的空间想象能力，这才是教师在教学中需要完成的教学项目。从初中学习的平面几何到高中的立体几何，圆锥曲线和一般平面曲线都隶属于“空间形式”的范畴，若是使用结构图表示如下所示：

高中阶段教材中的三视图引入，其目的是深化学生的空间思维意识，使得学生能在知识内容学习期间将各项知识内容整合在一起，在大脑中构建出完整的图形。学生在平时训练中，为了更好地锻炼空间观，建议购买巴克球，使用巴克球进行空间构造，做好图形的立体搭建。由于高中阶段开始涉及空间图形，所以空间感的培养很重要，初中阶段接触的图形多为二维图形，高中阶段在能力迁移的时候需要在二维的基础上多加一维空间，形成三维立体图形。

3.运算能力

数与数的运算是运算系统的基础，若能从义务教育阶段持续到高中阶段，就要在接触各项运算的过程中，形成较好的运算意识和运算能力，进而在解题的时候有所助力。

其实，有人会提出质疑，随着计算机的普及，人脑是否还有需要进行复杂的计算，相关数据使用计算机计算即可。其实计算机作为一项计算工具，能完成冗长的数字或者代数计算，但是在复杂计算上面计算机依旧不能与人脑媲美，计算机很多时候还需要人脑编码。

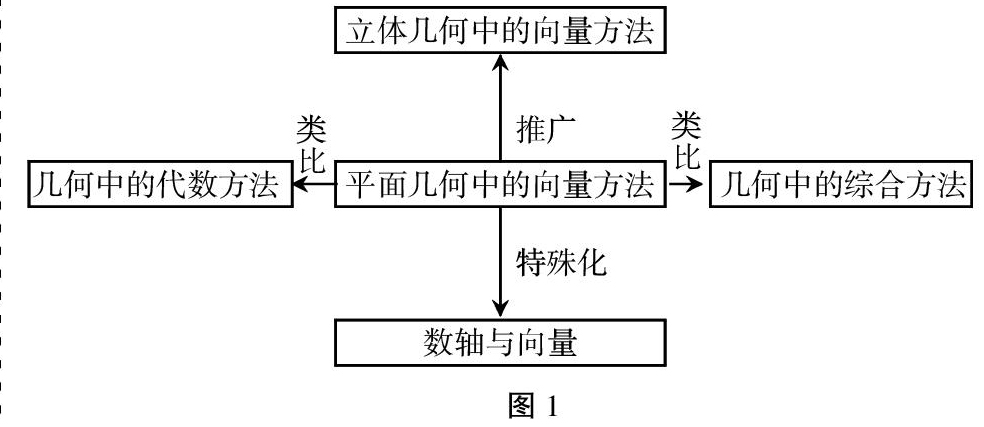
学生进入到高中阶段后，抽象运算让运算的复杂性加剧，教材中的部分内容不再是数字运算或者代数运算，每一块的知识都要通过运算的方式来获得。在一些具体的思维逻辑方面还需要通过类比、推广或者特殊化的方法将其定性。如，三角函数教学中解三角形边与角关系的时候，曲线率使用导数，直线方程表达都可以，若是这些定性的东西用量的方式表达出来，解题就会容易起来。

运算过程中所有的变化都要做到万变不离其宗，教材中虽然没有明确地说明要如何计算，使用何种计算方法，但真正的计算只有几种，课本中的相关例题都是经过筛选后获得的，是值得学生与教师推敲的。有的题目可能有一些简单的算法，虽然笨拙一点，但也能解答出来，但考试有时间限制，在平时的学习中学生就要在不断观察和总结的过程中，选择最优的方法，以给自己节约更多的解题时间。

（二）利用思维导图进行数学能力迁移与发展

在教学工作中，教师可以用思维导图的方式对学生进行引导，帮助学生展开知识点的学习和总结。思维导图具有简单、有效的特点，同时还具有很轻的趣味性，可以有效地吸引学生，促使学生主动开展学习活动。教学活动中，教师可以尝试让学生将学习过的知识点联系到一起，画出一个思维导图，将知识点有效地联系到一起形成一个完整的知识体系，使学生能够加强对知识点的有效记忆。防止学生由于知识点独立存在而造成记忆不清和混淆的问题。通过思维导图的应用，学生能够对知识点记忆更加深刻，并通过彼此之间的联系，对记忆模糊的知识点进行有效推理。在思维导图的帮助下，学生将会改善学习惯，对自身在学习中存在的问题进行纠正。

例如，教师可以使用思维导图对学生开展导数和微分相关知识点的教学工作。导数与微分都是微积分计算的基础知识，而微分内容更是近些年才刚刚加入到高中教学工作当中，具有一定难度的知识点内容。很多学生对于微分知识的学习存在着很大的困难。教师利用思维导图的方式便可以有效地将导数相关知识点与微分相关知识点联系到一起，减小知识点的跨越度，使知识点的教学工作难度得以下降。教师可以对思维导图的内容进行不断丰富和完善，使其与初中学习过的函数相关知识点联系到一起，帮助学生更好地对知识点间的关系进行梳理，使学生能够在心中拥有一个知识点的整体框架，使学生能够更好地进行发散性思考，同时还能够保障学生的发散思维能够与教学内容保持一致。

在思维导图的帮助下，学生能够对微积分的知识点定位进行有效掌握，降低对其的恐惧心理;还可以非常好地对初中函数知识点进行复习，使学生在学习新知识点的同时掌握旧知识点内容。在学生自己动手绘制思维导图的过程中，其可以自由地在其中添加自己感兴趣的元素，使各种知识点在大脑中形成良好的知识网络，加深学生对于知识点的印象。在初次使用思维导图的时候，教师要为学生讲解思维导图的绘制方式。引导学生使用不同颜色的笔去绘制思维导图，只要能够成功地形成串联，便可以实现灵活运用的目的。

使用思维导图开展教学工作，教师必须要对相关知识点进行深入思考，将初高中知识点形成有效联系，做好知识点的迁移工作，并在这一过程中使学生对知识点加强理解，使学生能够将不同的知识点融会贯通，更好地应用各种知识点解决实际问题。

初高中数学知识衔接中，學生对于数学知识点理解与应用是教师教学的重点环节。教师要通过各种方法的使用，帮助学生实现知识点的有效迁移，使学生能够在大脑当中形成完整的知识体系框架，促使学生通过努力学习掌握知识点间所具有的特殊联系，从而有效应用知识。

参考文献：

[1]徐静.承初中之基础，启高中之能力：初高中数学衔接教学方法的实践研究[J].数学学习与研究，2015（15）：159-160.

[2]罗金珍.数学语言互译能力的研究：基于初高中数学衔接的学习能力培养研究[J].考试周刊，2018（25）：73-74.

[3]齐海欣.新课程改革下初、高中数学衔接问题探究[J]. 环球人文地理，2014（14）：165-166.

[4]谭胜君.初高中数学衔接教学中的问题分析和对策探索[J].中学课程辅导（教学研究），2014（2）：81-82.

[5]赵永强.关于初高中数学衔接教学的探究[J].考试周刊， 2014（90）：60-61.

编辑段丽君

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。