《感知　规则　应用》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

感知　规则　应用

范文

谢蓓蓓

本节课是苏科版数学教材七年级上册第三章第四节的第一课时。本章内容从生活中引入代数式，以代数式的认识、运算以及应用为主线展开研究。合并同类项是本章的重点，其法则的应用是整式加减的基础，也是以后学习解方程、解不等式的基础。另外，合并同类项其实是有理数运算的延伸与拓展，是简化数学运算的常用方法，对于解决一些实际问题和进一步学习有着深远的意义。因此，这节课具有承上启下的作用。

一、从整体到部分，感受知识的必要性

建构主义认为，学生的学习应该建立在已有知识经验的基础上，教师需要为学生创设学习情境，以帮助者和促进者的身份引导学生主動发现、合作交流，从而获得新知识和新经验。

笔者将教材中计算学校校园占地面积的生活情境转化为数学内部的情境，分为以下几个问题。

问题1：在第二章，我们认识了有理数，学习了有理数的运算以及应用。类比有理数的学习过程，你觉得下面我们该怎样研究代数式呢？

问题2：3a+2a可以计算吗？

问题3：3a+2b可以计算吗？

问题1是希望学生感受数与式之间的联系，体会类比的数学思想，从整体的角度建立式类知识的研究路径。教师可以继续追问学生：该如何研究代数式的运算呢？此时，可以引导学生从运算分类的角度以及从简单到复杂的角度进行思考，从而确定研究的方向：从单项式的加法入手。

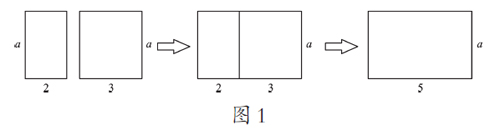
对于问题2，学生在已有知识经验的基础上，容易得出结果为5a，而教师此时一定要让学生说出自己的想法。在实际教学中，学生会有很多想法：有的学生会说3份a加2份a应该是5份a，他们其实是从物化的角度出发，联系生活实际进行思考的;有的学生则是提出可以利用乘法分配律将3a+2a写成（3+2）a。此时，教师更要引导学生从图形的角度来认识3a和2a，3a可以看作是边长分别为3和a的矩形，2a可以看作是边长分别为2和a的矩形，它们可以拼成边长分别为5和a的矩形（图1）。

接着，笔者提出问题3，引发学生积极思考，激发他们从不同的角度去说明3a和2b是不可以相加的，让学生生出单项式要分类的需求。

二、从感性到理性，感受知识的合理性

问题4：你能将下列单项式分类吗？说说你的理由。

（1）0;（2）a2;（3）-20a2;（4）-0.5x2y3;（5）-[12];（6）5x2y3。

问题5：你觉得什么样的单项式可以分为一类？

对于问题4，教师在课堂上应该给学生独立思考的空间，让他们可以根据自己的感知进行分类。学生通常有两种分类方法：第一种是根据单项式中有无字母，将（1）（5）分为一类，（2）（3）（4）（6）分为一类;第二种则是在前面分类的基础上，再根据字母的特征将（2）（3）和（4）（6）分开。学生在表达想法的同时体会了分类的数学思想，培养了数感。

到这里，学生已经对同类项的概念有了感性的认识。于是笔者接着追问：你觉得单项式2x3y2能和以上6个单项式中的哪些单项式分为一类？此时，学生的目光必定集中在（4）（6）这一类上，但是马上又能发现2x3y2和5x2y3的字母x和y的指数是不一样的，引发新的思考和判断。在学生思考的同时，笔者继续追问：你能说出一些和（4）（6）是一类的单项式吗？学生在刚刚思考的基础上很快就能举出例子。最后，通过问题5，让学生总结、补充，逐步明晰同类项的判断标准。

在刚才的探索中，学生已经对同类项的概念有了自己的感悟，接下来就是要将自己的感悟表达出来，从而归纳出同类项的概念：所含字母相同，并且相同字母的指数也相同，另外，几个常数项也是同类项。此时，笔者提出以下问题。

问题6：下列各组单项式是同类项吗？

（1）a与ac;（2）3x2y与-xy2;（3）a2与-2a2;

（4）23与-a3;（5）500与-1;（6）ab与ba;（7）b2a与a2b。

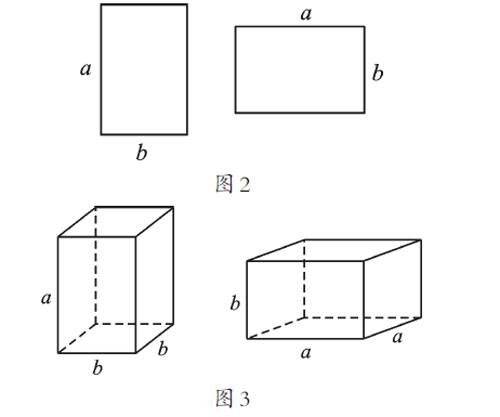
对于概念的教学，我们通常都是先创设出生活或数学的情境，然后与学生一起发现概念，再通过正例或反例辨析概念，明确概念的内涵和外延。所以，笔者提出了问题6。在实际教学中，学生对于（6）和（7）的辨析有些疑惑，而学生的纠结点就是教师最好的出发点。故笔者追问学生：你是如何思考的？学生通常会从同类项的概念或者乘法分配律的角度进行解释，也有学生受到之前的启发，从图形的角度来表达。比如ab可以看作是边长分别为a和b的矩形，ba可以看作是边长分别为b和a的矩形，它们是同一种图形（图2）;b2a可以看作是底面边长为b、高为a的长方体，而a2b可以看作是底面边长为a、高为b的长方体，它们不是同一种图形（图3）。

学生通过思考一系列层层深入的问题，在观察、思考、归纳和辨析的过程中，从感性到理性的角度逐步感悟同类项的概念。在教学中，教师应该有意识地帮助学生体会数形结合等数学思想，提升直观想象等核心素养。

三、从认识到运用，感受知识的一致性

教师在前面学习的基础上提出新问题。

问题7：下列式子能运算吗？如果可以，请说出运算结果。

（1）a2+2a2;（2）-x2y3+4x2y3;（3）3x2y-xy2;

（4）2ab-ac。

问题8：你能总结归纳出单项式加法法则吗？

问题9：请尝试计算2a2-3ab+5-2a2-3ab-7。

学生通过问题7的运算，再次思考，并明确什么样的单项式才能相加。笔者通过问题8，让学生归纳出单项式的加法运算可以分为同类项相加和非同类项相加两种类型，如果是非同类项，则不能合并;如果是同类项，则将同类项的系数相加，所得的结果作为系数，字母和字母的指数不变，并指明这就是合并同类项的法则。最后，笔者利用问题9，让学生尝试利用合并同类项的法则进行整式的加减运算，提高学生的应用能力。教师在学生分享自己的做法时，可以让学生读读题目，类比有理数的运算，将减号看作是省略加号的符号;可以利用投影，对学生的作业进行修改，规范解题过程;可以多关注运算有差错的学生，将个别辅导和合作纠错落到实处。接下来，笔者再给出一道练习“-2m2n-[13]mn2-1+[23]n2m+m2n”，要求学生独立完成，以提高学生的运算能力。

合并同类项法则的应用是整式加减的基础，也是以后学习解方程、解不等式的基础。而合并同类项的法则是建立在数的运算的基础之上，因此，教师需要适时引导学生在学习过程中建立数与式的联系，感受数式通性，体会知识的一致性。

四、从当下到未来，感受知识的延伸性

至此，学生对同类项的概念以及合并同类项的法则已经有所掌握，并且对合并同类项在单项式运算中的地位有了一定的认识。因此，教师可以在学生小结本节课收获的基础上提出最后一个问题。

问题10：你觉得以后我们还会学习什么知识？

这个问题给了学生更为广阔的思考空间。教师可以引导学生从运算方式的角度或者从简单到复杂的角度思考、交流、表达，逐步完善式类知识的结构，展望幂的运算、单项式和多项式以及多项式和多项式的运算、分式的运算等知识，让学生对未来的学习充满期待。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。