《打开圆这把锁的“金钥匙”》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

打开圆这把锁的“金钥匙”

范文

段昆山

摘要：圆的证明与计算是各省市中考的高频考点.本文从“遇到切线，连半径”“遇到弦，作弦心距”“遇到直径，构造直径所对圆周角”“遇到特殊的几何图形，作垂直”四方面阐述添加辅助线的方法.要解决好此类题目需要有扎实的基础知识，较强的分析、推理能力，更需要抓住辅助线这个“金钥匙”.

关键词：辅助线;几何图形;直径

历年来圆的证明与计算都是各省市中考的热点，其试题主要以圆为载体，结合三角形、四边形、三角函数、相似等知识.涉及转化、方程思想，难度大、变化多，很多同学感到无从下手.其实我们只要抓住辅助线这个“金钥匙”，就能够打开圆这把锁.

钥匙1 遇到切线，连半径

已知条件中，有切线，可以连接圆心和切点即半径，利用切线性质、弦切角定理，构造垂直、角相等.

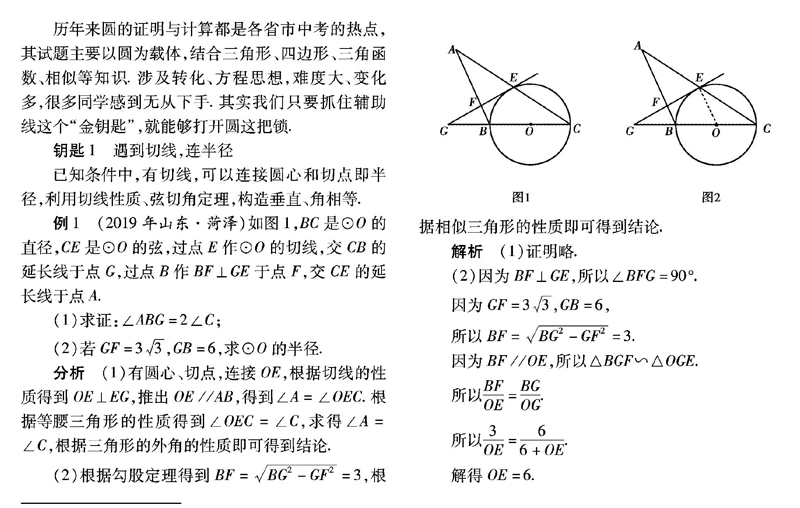
例1 （2019年山东·菏泽）如图1，BC是⊙O的直径，CE是⊙O的弦，过点E作⊙O的切线，交CB的延长线于点G，过点B作BF⊥GE于点F，交CE的延长线于点A.

（1）求證：∠ABG=2∠C;

（2）若GF=3 3，GB=6，求⊙O的半径.

分析（1）有圆心、切点，连接OE，根据切线的性质得到OE⊥EG，推出OE//AB，得到∠A=∠OEC.根据等腰三角形的性质得到∠OEC=∠C，求得∠A=∠C，根据三角形的外角的性质即可得到结论.

（2）根据勾股定理得到BF=BG2-GF2=3，根据相似三角形的性质即可得到结论.

解析（1）证明略.

（2）因为BF⊥GE，所以∠BFG=90°.

因为GF=3 3，GB=6，

所以BF=BG2-GF2=3.

因为BF//OE，所以△BGF∽△OGE.

所以BFOE=BGOG.

所以3OE=66+OE.

解得OE=6.

所以⊙O的半径为6.

评注圆的切线垂直于经过切点的半径，若出现圆的切线，必连经过切点的半径，得出垂直关系.本题考查了切线的性质，相似三角形的判定和性质，等腰三角形的判定和性质，正确地作出辅助线是解题的关键.

钥匙2 遇到弦，作弦心距

已知条件中有弦，可以作弦心距，利用垂径定理，结合勾股定理、三角函数等知识，求线段长度、角的度数.

例2 （2019年浙江·金华）如图3，在OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D.

（1）求BD的度数;

（2）如图3，点E在⊙O上，连结CE与⊙O交于点F，若EF=AB，求∠OCE的度数.

分析（1）如图4，连接OB，证明△AOB是等腰直角三角形，即可求解.

（2）由△AOB是等腰直角三角形，可得OA=2t，HO=OE2-EH2=2t2-t2=t，即可求解.

解析（1）略.

（2）如图5，连接OE，过点O作OH⊥EC于点H，设EH=t，

因为OH⊥EC，所以EF=2HE=2t.

因为四边形OABC是平行四边形，

所以AB=CO=EF=2t.

因为△AOB是等腰直角三角形，

所以OA=2t.

则HO=OE2-EH2=2t2-t2=t.

因为OC=2OH，所以∠OCE=30°.

评注本题主要利用了切线和平行四边形的性质，其中问题（2）要利用问题（1）中△AOB是等腰直角三角形结论.

钥匙3 遇到直径，构造直径所对圆周角

已知条件中有圆的直径，常构造直径所对的圆周角.利用直径所对的圆周角是直角，通过勾股定理、三角函数、相似三角形等知识求解.

例3 （2019年辽宁·沈阳）如图6，AB是⊙O的直径，BC是⊙O的弦，直线MN与⊙O相切于点C，过点B作BD⊥MN于点D.

（1）求证：∠ABC=∠CBD;

（2）若BC=4? 5，CD=4，则⊙O的半径是.

分析（1）如图7，连接OC，由切线的性质可得OC⊥MN，即可证得OC//BD.由平行线的性质和等腰三角形的性质可得∠CBD=∠BCO=∠ABC，即可证得结论.

（2）连接AC，由勾股定理求得BD，然后通过证△ABC∽△CBD，求得直径AB，从而求得半径.

解析（1）略.

（2）连接AC，在Rt△BCD中，BC=4 5，CD=4，所以BD=BC2-CD2=8.

因为AB是⊙O的直径，所以∠ACB=90°.

所以∠ACB=∠CDB=90°.

因为∠ABC=∠CBD，所以△ABC∽△CBD.

所以ABBC=CBBD.即AB4 5=4 58.

所以AB=10.所以⊙O的半径是5.

评注本题考查了切线的性质和圆周角定理、三角形相似的判定和性质以及解直角三角形，作出辅助线构建等腰三角形、直角三角形是解题的关键.

钥匙4 遇到特殊的几何图形，作垂直

已知条件中有特殊的三角形比如含30°，45°的三角形、含45°，60°的三角形或利用作垂直构造等腰直角三角形，利用三角函数、相似、面积公式等知识求解.

例4 （2018年浙江·温州）如图8，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在⊙O上.

（1）求证：AE=AB;

（2）若∠CAB=90°，cos∠ADB=13，BE=2，求BC的长.

分析（1）由折叠得出∠AED=∠ACD，AE=AC，结合∠ABD=∠AED知∠ABD=∠ACD，从而得出AB=AC，据此得证.

（2）作AH⊥BE，由AB=AE且BE=2知BH=EH=1.根据∠ABE=∠AEB=∠ADB知cos∠ABE=cos∠ADB=BHAB=13，据此得AC=AB=3，利用勾股定理可得答案.

解析（1）略.

（2）如图9，过A作AH⊥BE于点H.

因为AB=AE，BE=2，所以BH=EH=1.

因为∠ABE=∠AEB=∠ADB，cos∠ADB=13，

所以cos∠ABE=cos∠ADB=13.

所以BHAB=13.

所以AC=AB=3.

因为∠BAC=90°，AC=AB，所以BC=3 2.

评注本题主要考查三角形的外接圆，解题的关键是掌握折叠的性质、圆周角定理、等腰三角形的性质及三角函数的应用等知识点.

圆的证明与计算，难度大、综合性强、涉及的知识面广，是初中数学中最重要、最核心、纵向和横向联系规模最大的内容之一.要解决好此类题目需要有扎实的基础知识，较强的分析、推理能力，更需要抓住辅助线这个“金钥匙”.

（收稿日期：2019-08-30）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。