《浅谈小学数学概念的教学策略》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

浅谈小学数学概念的教学策略

范文

夏士勇

【摘要】数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映。它是进行一切数学学习活动的基础。但在日常学习中，学生面对这些抽象的概念“无所适从”，构成学习数学的障碍。试图从概念教学的现状入手，结合自己的教学实践，从“概念的引、建、用”三方面展开，探寻小数学概念教学的一些基本策略，以帮助学生更好理解掌握数学概念。

【关键词】数学概念；教学；策略

一、小学数学概念教学中的一些现象

1. 过度人文，干扰较多。新课程提出要关注人文教育，我们有的老师在情景设计中，过多地设计了数学以外的因素，如在二年级《乘法的初步认识》的情景视频中出现：在热烈的音乐声，观察人声鼎沸的游乐场，有惊险刺激的冲浪，险象环生的蹦极，瞠目结舌的“扭转乾坤”，热血沸腾的过山车等等，老师问：你看到了什么？有什么想说的？学生答道：“很好玩”，“太有意思了，我也想去”，“好危险啊”上述的情景虽然令人振奋，但大量充斥了与教学内容无关的信息，干扰了学生对概念的理解。

2. 过度操作，内化太少。动手操作，是理解概念一种很好的手段。我们一位老师，在执教“20以内数的认识”时，为了让学生建立“十”这个单位概念，用了大量的学具，安排了数小棒，数本子的页数，数小豆豆，数回形针，本意是让学生通过不同物体的计数，充分的建立“十”计数单位。但一个循环下来，学生忙的不亦乐乎，教师急得满头大汗，一年级小孩子看见这么多学具，都兴奋不已，注意力都集中到学具操作上，不会去思考数的结果，把老师的任务抛到“九霄云外”。

3. 过度过程，结果混乱。新理念指导我们，过程与结果同样重要，过程教学，是必须关注的。本人曾听一位老师执教“两位数乘两位数”，在研究12×24时，老师为了展示算法多样化这一过程，“绞尽脑汁”展示每一种算法：有（10+2）×24，（20+4）×12，24×6+24×6，（30-6）×12，12×3×8，12×4×6，24×2×6，24×3×4，2×6×3×4……满满写了一黑板，最后的结果，学生糊里糊涂，到底选哪种？老师只是说：“请自己选择喜欢的算法。”似乎，把学习的主动权利都交给学生，但学生最后“无所适从”。

上述现象给学生在概念学习中造成很大的困难，这就需要我们能认识到这些困难并在教学中采取多种措施帮助学生正确的方式进行概念学习，将数学概念在学生的头脑中更牢固、更深刻地建立起来。笔者结合自身的教学实践，来谈一谈对概念教学的一些看法：

二、重视概念学习中的“引”

1. 从熟悉的生活中引入

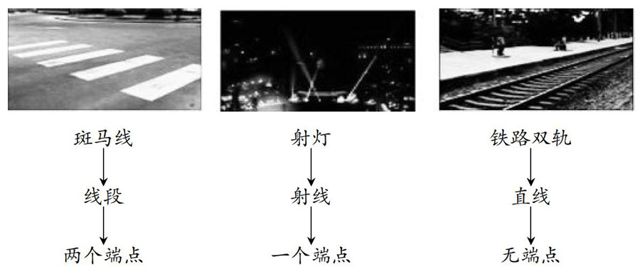
数学概念源于生活，我们就要从源头引入，找到知识的原点，选用学生所熟悉的事件，把抽象的数学概念和具体的事例相结合，逐步引入新概念。如教学线段、射线、直线概念时，从学生熟悉的斑马线、射灯、铁路轨道引进线段、射线、直线，再比较他们之间的不同从而抽象出数学概念。这样引入概念，形象、熟悉、自然、流畅，使学生能更加投入概念的学习当中。

2. 从简约的计算中引入

数学的教学离不开计算，我们应该通过对运算的观察分析，发现其中蕴含的本质特征，揭示数量或形的本质属性，达到引出概念的目的。比如教余数概念和与除数关系时，出示例题：一共有16盆花，每组摆5盆，可以摆几组？多几盆？如果是17盆，18盆，……，24盆，25盆呢？我们安排这样设计：

（1）引导学生列式算一算。

（2）再引导学生讨论：观察余数与除数，你们发现了什么？

15÷5=3（组）

16÷5=3（组）……1（盆）

17÷5=3（组）……2（盆）

18÷5=3（组）……3（盆）

19÷5=3（组）……4（盆）

20÷5=4（组）

21÷5=4（组）……1（盆）

23÷5=4（组）……3（盆）

22÷5=4（组）……2（盆）

24÷5=4（组）……4（盆）

（3）归纳总结：剩下不能再分的数才叫余数，感知余数要比除数小。

三、关注概念学习的“建”

1. 借助模型，建立概念

在数学概念的认识过程中，我们可以借助模型帮助学生建立数学概念。例如，我们的伊老师在教《千以内的数的认识》时，就运用方块模型帮助学生建立一千的概念，理解数的意义。

我们看到通过方格模型的演示，让学生体会10个一是十，10个十是一百，10个一百是一千，通过几何图形的点、线、面、体，使学生在头脑中建立“一、十、百、千”的映像，在学生的头脑中建立一个清晰的模型“满十进一”，对于学生理解基数单位和进位制是有很大好处的。

2. 循“理”入法，理解概念

小学生在计算过程中常出现许多错误。这些错误多数由于概念不清、算法不明、运算粗心等原因造成的，需要教师仔细分析，找到策略。比如笔者在教“一位数除多位数”时深感头疼，学生总是不明白。有一回见到曹培英先生介绍的循理入法策略，引导学生循“理”入法（即依据算理，理解算法），以“理”驭法（即根据算理，掌握算法），令人耳目一新。他采用小棒作教具，通过操作、演示，使长除的过程步步有理有据，这个过程叫“商乘减落”，具体如下：

这个效果非常好，学生很容易感悟“分小棒”的过程与竖式计算过程的一致性。遵循着算理，“商减乘落”的操作过程变得十分形象、生动，学生很容易理解竖式除法概念的过程。

3. 展现历程，掌握概念

我们都知道，概念的建立最好能展现其原来的进程，这样对于学生的理解概念达到“事半功倍”之效果。例如在“用数对确定位置”教学中，本人如下设计：

（1）情景提问，引发需要。班级座位图：你说说图中小朋友的位置？你是怎么数的？楼房的层数问题：第几层第几号？

（2）抽象点子图。把情景中两个实际问题，抽象成点子图。

（3）列行描述，认识数对。①体会繁琐：老师报4个同学的位置，请你写下来。说一说记录的感觉，有什么好的方法？②体会用数对表示位置。学生：四字表示，3行2列、5行8列；两数表示32 58……③对比：如果用32 58给别人看，能明白吗？需要怎样调整？

（4）揭示概念：用逗号隔开，表示3，2 5，8。又因为用两个数字表示，两边加上括号——（3，2）（5，8）

四、感悟概念学习的“用”

1. 设计变式，把握本质

教学中，我们所提供的事例或材料，应不断地变换呈现形式，改变非本质属性，使本质属性恒在，由此帮助学生准确形成概念。如教“圆的面积”时，在学生明白圆的面积含义的基础上，设计比较哪个阴影部分面积大的问题。这对学生来说，这是一个充满挑战性的问题，要求出阴影部分面积，学生需要仔细分析正方形与各扇形面积的关系，关系明白了，结果自然也知道了。再让学生发现他们的阴影部分的面积居然相等，更进一步理解圆面积的深一层含义。

2. 合理分类，化繁为简

每一块数学知识包含的概念极其丰富，我们通过分类可以使大量繁杂的知识系统化、条理化，有助于孩子更好地掌握知识和形成系统的知识体系。如：三角形分类整理。

（1）按角分：锐角三角形、直角三角形、钝角三角形。

（2）按边分：不等边三角形、等腰三角形。

通过分类，学生很清楚掌握三角形这么多相似的概念，以及它们之间的紧密联系，从而使学生有效地感悟概念，深刻理解概念。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。