《给予一方池塘，积蓄思维发展的能量》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

给予一方池塘，积蓄思维发展的能量

范文

施宇红

【摘要】数学教学中存在许多思维训练的无效现象：有些教师的思维训练只光应付例后的巩固练习，学生的思维得不到发展;有些思维训练题难度偏大，造成教学的冷场;有些思维训练流于形式，用优生的思维代替全班学生的思维，形成学生思维的虚假活泼;有的思维训练不重视思维训练的开放性，削弱了训练的有效性。“每日思训”实践活动的研发，旨在体现知识的连贯性、情境性和应用性，重在培养学生的思维能力，增强学生思维的兴趣性、主动性，关注思维发展的延续性、创新性等，全面促使高层次思维的形成，为学生的终身发展奠定坚实的基础。

【关键词】每日一题思维品质思维能力创新教育实践

“热带鱼故事”大家耳熟能详，鱼儿在一尺来宽、两尺来长的发展空间里，纵然使出浑身解数，也注定只能在限定的范围内活动，它们吸收的养料与水分只能限定在鱼缸之内，在这样的环境中，鱼儿只能选择顺从。然而当鱼缸不小心被打破，鱼儿被放进喷水池中，两个月后，那些鱼竟然都由三寸来长疯长到了一尺！反思教师对于学生思维的培养不也正是如此？教师给予学生一个怎样的思维发展舞台，学生就会得到怎样的发展。学校的空间固然很狭小，但是学生所受到的教育却取决于教育者的高度。如果教育者能够立足学生的长远发展，站在学生思维成长的角度施以教育，那么就如同给予了学生一方池塘，为学生的未来学习积蓄了足够的能量。

笔者有幸接手了十几年教学生涯中的第一届一年级学生，为了在学生的起始年级培植思维的幼苗，关注其内隐的思维习惯的培养，使之在学习中勤于思考、乐于思考、恒于思考，真正成为思考领域里的小劳动者，笔者用一年的时间和学生进行了“每日思维训练”的探索之旅，下面结合实践谈谈笔者对如何开展每日思维训练活动的几点思考。

一、培育思维的延续性

在数学教学中，教师首先要高屋建瓴、高瞻远瞩去了解学生们在这个阶段学习了哪些知识点，在后续的学习中还会延伸到哪些面，在学生的数学学习中，哪些是重点，哪些是难点，这样才能对学生的数学发展、思维发展有一个整体认识。在了解知识脉络的基础上再想到学生思维培养时，就会有一个宏观上的把握了。

例如：在“数与代数”领域，当学生一年级学习了10以内的加减法后，“排队问题”在学生的思维提升题中经常出现，下面呈现笔者对排队问题的几次合理设计：

一年级上册： 12月6日

小朋友排队，我的前面有2人，后面有1人，这队一共有多少人？

（建议：先模拟场景排好队，让学生感知要求一共有多少人，要把排在前后的人数加起来，再加上自己）

举一反三：

（1）小朋友排队，我的前面有3人，后面有4人，这队一共有多少人？

（2）小朋友排队，我的前面有3人，后面有6人，这队一共有多少人？

说明：第一次呈现排队问题的类型，让学生感知一队的总人数为前面的人加上后面的人还需加上自己。

一年级上册： ?12月13日

小朋友排队做操，从前面数起，小红排在第2个，从后面数起，小红排在第3个，这队一共有多少人？

举一反三：

（1）小朋友排队做操，从前面数起，小红排在第3个，从后面数起，小红排在第5个，这队一共有多少人？

（2）小朋友排队做操，从前面数起，小红排在第4个，从后面数起，小红排在第2个，这队一共有多少人？

说明：排队问题除少数一个自己，另一种典型类型就是多数一个自己，让学生感知一队的总人数除前面的人加上后面的人还需加上自己这一类型之外，还可用两数相加再减去自己（自己算了两遍）。

一年级上册： 1月17日

1. 小朋友排队，小平的左边有4人，右面有8个人，这队一共有多少人？

2. 小朋友排队，从左数过来，小明排在第4个，从右面往左数是第8个，这队一共有多少人？

说明：一年级上册所涉猎的三次排队问题，从分到合，从单一到混合，完成了一系列正向的思维引导。引导学生正确地分析，建立相应的数学模型，从而培养推理能力。

一年级下册： 3月3日

10个小朋友排队回家，小明前面排了5个小朋友，那么他的后面排了几个小朋友？

举一反三：13个小朋友排队回家，小明后面排了7个小朋友，那么他的前面排了几个小朋友？

说明：在学完10以内的减法后，呈现“排队问题”中的逆思维类型的练习，让学生知道要求排队中“我”前面或后面的人数需总人数减去前面（后面）的，再减去1（自己），就能求到排在后面（前面）的小朋友的人数。

反思：我們会发现数学学习真的是一个融会贯通的体系，是一种思维上的延续，而不是单独的某一个点、某一个段、某一个篇章。前期，没有很好地铺垫、理解，后期的问题就会接二连三;前期没有正确、有效地思维训练，后期只疲于做题，成效也是甚微。反之，如果我们坚持在学生们的每一个年段，每一个学期都会涉及，由浅入深、层层递进，逐渐地抽象、推理，从而建立模型，有助于其思维深层次发展。

二、唤醒思维的自主性

或许有人会质疑：一年级学生这么小，字都看不懂，怎么去朝你既定的方向去发展？一开始的思维训练笔者没有强制学生完成，但每回认真做思训并做对的学生笔者都给他盖个漂亮的小印章，并不断地鼓励和表扬他，并立下规则，凡能得到10个小印章的学生，可得到一张智慧卡，满了五张智慧卡就可以进入班级明星榜，满了10张智慧卡到学期末可获得“数学智慧星”的奖状，其实每个学生都有一种内在的积极向上的驱动力，在每日思维训练试行一个星期后，家长就自发地帮助学生养成良好习惯。

当然，要唤醒思维的自主性，除了外在的一些激励机制，最本质的还需激发他们的学习兴趣。我们都知道：“兴趣是最好的老师。”培养低年级学生的学习兴趣是提高其思维能力的重要前提。

一年级下册： ?3月7日

有12人玩老鹰捉小鸡的游戏，已经捉住了5只小鸡，还有几只小鸡没被捉住？

举一反三：有17人玩老鹰捉小鸡的游戏，已经捉住了9只小鸡，还有几只小鸡没被捉住？

说明：我们知道，老鹰捉小鸡的游戏一定会有一个人当老鹰，一个人当母鸡。一共有12人玩游戏，我们现在知道小鸡被抓住了5只，那么还有12-5-2=5（只）。

反思：如今，我们难以看到翱翔的老鹰了。现在的学生也不玩“老鹰捉小鸡”游戏了，即便是会玩的也仅仅把它看成一个游戏，忽略游戏背后所隐藏的数学问题。在抽象的文字面前，被动地给予只会让多数学生无暇深思;笔者在设计此类思训题时，课间先带学生们在一种和谐的欢乐气氛中愉快地去游戏，再提炼相关思维题型，充分激发学生的学习兴趣，激活学生的思维，让学生真正内化“2”的含义。设想我们平时的数学学习仅有大量的练习，什么游戏也没有，只有批改下来的勾与叉，学生们会有兴趣吗？小学生的思维正处于以具体形象思维为主逐步向抽象思维过渡的阶段，作为教育者的我们在数学教学中应根据学生思维的发展规律，尽量创造条件，充分运用各种有效的教学手段和方法，启发引导学生积极主动地参与学习的过程，帮助学生积累鲜明、丰富的表象，从中获取知识发展思维。

三、尊重思维的独特性

众所周知，小学生的逻辑思维能力比较弱，特别是低年级学生更依赖于直观的思维，而数学学科又具有较强的抽象性和逻辑性。因此，我们希望学生能够用易于理解的方式呈现抽象的数学问题。

一年级上册： 12月24日

红红家住在三楼，她每上一层楼用7秒，她从一楼到家要几秒？

举一反三：

（1）明明家住在三楼，他每上一层楼用9秒，她从一楼到家要几秒？

（2）东东家住在四楼，他每上一层楼用10秒，她从一楼到家要几秒？

说明：学生的创造性真的是让大人颇为感慨，借助一些简简单单的符号和数字，楼梯问题便轻轻松松地解决了。

一年级下册： 4月15日

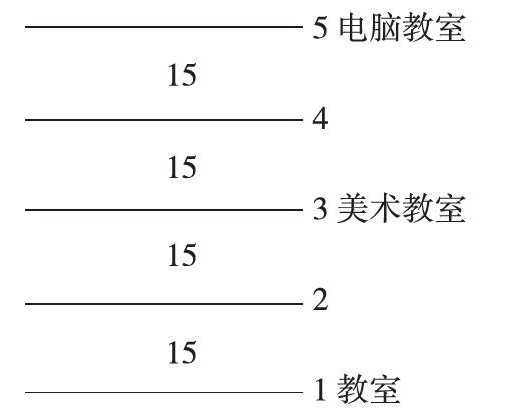
力力的教室在一楼，美术教室在三楼，电脑教室在五楼，每一层有15个台阶。力力从教室到美术教室要走（）个台阶，从美术教室到电脑教室要走（）个台阶。

反思：像这类生活中的间隔问题在小学阶段反复出现，复杂的条件很容易让人心生畏惧。看看我们一年级学生的智慧，很有数学味儿，全是线条和数字，多有趣，一条线代表一层，五条线就是五层，从1层到3层，要走两层楼梯，每层楼梯都有15个台阶，两层楼梯就是30个台阶。从美术教室到电脑教室，也要走两层楼梯，结果也是30个台阶。学生们借助数形结合思想中的图形直观手段，在画图中理解题意，让看似不能解决的问题轻轻松松地解决。正如著名数学家华罗庚说过：“数缺形时少直观，形缺数时难入微。”由此可见，教师在教学中要注重引导学生将抽象的数学问题直观化、繁难的数学问题简洁化，鼓励学生标新立异，培养思维的独特性。

四、激活思维的可能性

对于低年级学生，他们目前所面对的数学问题情境都是图文并茂的，有生动的情境，有表格的呈现，这些丰富的形式都会过渡成纯粹的语言文字描述，这有待我们逐步培养。但不管是外显的还是内隐的数学问题，都需让学生的思维活动具有“含金量”，其关键还是要有意识地让隐形的探究逐步浮出水面，鲜亮起来。

说明：找规律填数是小学阶段常见的题型，第1题比较简单，一看到题目，学生就能观察到2、4、6、8都是双数，每2个数之间相差2;第2题，从大到小，而且都是单数;第3题在解答这类题目时，学生就要运用函数思想，依次多1、多2、多3，依次类推;第4题学生一开始会有些疑惑，不断地猜测、检验，失败了再猜测再检验，最终找到正确的解法：就是前两个数相加的和等于第三个数。其实这个数列就是数学上著名的斐波那契数列，当笔者告知学生们你们都有数学家的头脑，和数学家的发现一样时，学生脸上绽放出自信而灿烂的笑容。

反思：法国教育家第斯多惠说：“一个不好的教师奉送真理，一个好的教师则教人发现真理。”虽然说，小学生学的数学很初等，很简单，但尽管简单，里面却蕴含了一些深刻的数学思想。如果我们在低年级时把自信送给每一个学生，给学生充足的思考时间，在学生内心深处培植探究的种子，可以让学生拥有一颗数学的大脑，学会数学地思考，学会理性地看待问题，相信学生在其成长的路上定能收获秋后的硕果！

五、追寻思维的超越性

在平时的教学中，学生思维发展的方向和立足点有很多，教师没必要让学生一股脑儿地多做题或钻难题。作为教育者的我们，也可根据学生当天所学内容的重难点、容易混淆的知识，或从错误的解题过程中发现思维误区的角度来设计思训题，帮助学生加强数学思想方法的渗透，也可以结合“生活與数学”这些实践作业，更可以跳出书本，从学生的“玩伴”中开发学生的数学游戏，从而全方位地发展思维、提高能力。

“数学与生活”的实践延伸板块一直是我校数学节日文化所重点研究的方向，一年级综合领域的思维训练关键是让学生想要动手，乐于动手，可以融合于我们学生的生活日常。一年级上学期，我班尝试开发的挑花棒课程、魔尺课程，就活动效果来讲，看着学生们课间走路的时候还美美地、痴痴地拿着魔尺玩，教师的心也跟着“甜”化了，学生们的智慧在指尖上无时无刻地流淌着，学生们动手又动脑，哪能不益智！挑花棒、魔尺等这些实践活动的研发，都是为了让学生们获得初步的数学活动经验，增强学生的动手能力，也让学生们感受到了数学的魅力和乐趣！

赞可夫说过：“教会学生思考，对学生来说是一生中最有价值的本钱。”在小学数学教学中，我们应有目的、有计划地对学生实施思维训练，由浅入深，多视角、全方位地启迪学生思维，从“思维品质”的层面入手，研究“思维能力”的培养和提升，探求学生们思维过程的小秘密。无论这过程是简单还是复杂，我们都要认真对待，一步一步地仔细分析，从低年级开始，从现在开始，读懂学生的思维过程，掌握学生的思维特点，那么学生的发展就不仅仅是分数的取得那么狭隘，而是更广阔的一片天空。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。