《创想学习活动：为深度理解而设计》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

创想学习活动：为深度理解而设计

范文

时敏

摘要：创想学习是儿童在特定的学习情境中，依托丰富多样的活动，经过个性化思考和创造性想象，构建知识和方法的学习过程。数学创想学习活动应给学生预留足够“大”的创想空间，这要求教师在设计时遵循“大数学”构思、“大单元”规划、“大框架”建构等原则;可按照启发设问、组织探究、迁移发散、练习反馈、形成结构5个环节铺设创想学习的路径。

关键词：创想学习学习活动教学设计《分数的基本性质》

创，即创造、创新;想，即联想、想象。“创想”指创造性想象。创造性想象不是对已有表象材料的复现，而是有意识地对原有知识和经验进行加工、改造和整合，从而在头脑里创造出新事物（形象）的过程。

创想学习是儿童在特定的学习情境中，依托丰富多样的活动，经过个性化思考和创造性想象，构建知识和方法的学习过程。创想学习活动顺应儿童天性，优化学习方式，改善思维品质，提升解决问题的能力，是一种富有情趣和智慧的活动。

小学生学习数学有其认知规律，能力发展具有不平衡性，对学习方法和路径接受和掌握的程度參差不齐，需要教师在教学设计与实施时有的放矢地进行阶梯式的推进和训练，才能悟得创想学习的真谛。因此，小学数学教师要遵循学生的认知特点，整体把握数学内容，设计好创想学习活动，让学生感知创想学习的魅力，引导学生用自己独特的方法解决数学问题，涵育数学核心素养。

一、设计原则——预留创想空间

数学知识有系统的内在逻辑结构，学生学习时，很多时候并不能“胡思乱想”，但掌握数学知识的方法可以多样化、“标新”，解决数学问题的路径可以多渠道、“立异”，对未知数学知识可以充满“奇思妙想”。所以，数学创想学习活动应给学生预留足够“大”的创想空间，这要求教师在设计时遵循以下几个原则：

（一）“大数学”构思

“大数学”构思是指，要“跳出数学”设计小学数学创想学习活动，将和本阶段、本单元数学内容相关的知识都包含进去，给学生更多的数学感知，如提供更多的数学应用实例，揭示生活、其他学科中数学思想方法的渗透，从而让学生认识到所学数学知识有广泛的应用价值，而非狭隘的、机械的局部数学知识。

（二）“大单元”规划

“大单元”规划是指，要充分挖掘数学知识之间的内在联系，一体化地设计系列活动，将数学知识联结成一张“网”。这张“网”是四通八达的，通过不同的路径可以实现知识之间不同形式的迁移互通，增加学生学习数学的方向感和整体感。

例如，教学“梯形”相关知识时，不能就梯形概念讲梯形，而应引导学生首先观察丰富的具体的梯形，然后将这些梯形进行类比、分析、简化，抽象出梯形的基本特征，进而思考梯形与其他平面图形（如三角形、四边形等）的关系，发现梯形面积计算公式的通用性。

（三）“大框架”建构

“大框架”建构是指，在具体到某一个知识点的设计时，对教学内容只做大框架的预设，留给学生更广阔的创想空间;对教学目标进行“大环节”“大问题”的确定，每一个环节都给学生更多探索、实践的自由度，减少灌输的痕迹，增加对核心问题的深度思考和持续探究，进而对数学知识形成带有个性特征的理解。其间，要帮助学生掌握多种学习方式，如通过动手做验证猜想，通过“试错”辨析正误，通过分析进行总结，等等，助力学生形成对数学知识的深度理解，掌握解决问题的策略和技能。

二、设计实施——铺设创想路径

小学数学创想学习活动的设计与实施，一般包括启发设问、组织探究、迁移发散、练习反馈、形成结构5个环节，引领学生经历有始有终的创想学习过程。下面以苏教版小学数学五年级下册《分数的基本性质》一课为例具体说明。

（一）启发设问：问题开放

所有的创想都是由问题开始的，提出一个有思维空间的问题是引入创想学习的第一步。在开始每一个数学知识的学习之前，教师要知道学生已经有了哪些知识基础，将要学习哪些新的知识，以及后续还有哪些相关联的知识。即基于可迁移的知识来设计“大数学”问题，用有开放度的问题来引发学生的思考。这个问题的答案不是唯一的，而是多元的，在这些答案中可以找到新旧知识之间的内在关系，为创想学习指引方向。

本课课始，教师出示邮票图（如图1），提问：深色邮票部分可以用什么分数表示？

学生回答后，教师追问：你是怎么看出来的，说一说你的想法。

学生展示两种表示方式（2/3和6/9），并知道二者相等。

教师引入：那么问题来了，这两个分数分子和分母都不相同，怎么会大小相等呢？这就是我们今天要学习的——分数的基本性质。

（二）组织探究：体验丰富

数学创想学习活动特别需要学生敢想、敢创，并且需要一定的思维含量，掌握一定的创想技能。教师在设计时就要尽量让问题主题化、系列化，让探究活动不是零敲碎打，而是围绕研究主题展开，形成“大框架”，并给予较长的探究时间，使活动体验更为丰富。这样，活动更完整、有序，更有利于持续地培养学生的创想能力。同时，教师要因势利导地教给学生联想、类比、猜想等方法，发现已知和未知、现象与本质之间潜在的关联，找寻其中的规律。这个过程可以是一个综合的过程，也可以分为一个个阶段性的发现过程，让学生不断地总结提高。

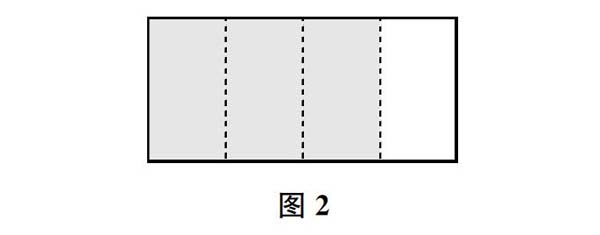
本节课中，承接“这两个分数分子和分母都不相同，怎么会大小相等呢？”的启发性问题，教师出示图2，提问：这里有一张长方形纸，阴影部分用几分之几表示？

学生回答后，教师布置开放的活动：找出和（3/4）相等的分数，可以折一折、画一画等。

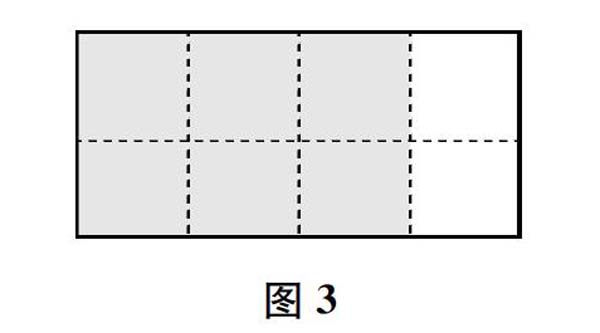
学生操作后，教师选取一位学生的做法（如图3）引导交流：你是怎么折的？你得到的分数是多少？你这样折其实就是把原来的每一份再平均分成了几份？

然后，教师引导学生整理思路：原来的分子、分母同时乘几？得到的分数是几分之几？并根据学生的回答形成类似图4的板书。

教师组织学生进一步研究：（1）如果不折纸，要找到与34相等的分数，有没有简单的方法？（分子、分母同时乘相同的数）（2）分子、分母同时乘7，相等吗？分子、分母同时乘9呢？分子、分母同时乘100呢？

小结：看来，用这种同乘一个数的方法，确实可以找到与34相等的分数。

这样的设计下，学生的经历是丰富的——不同的学生有不同的算法和例子，但都能分析得出其中有隐藏的规律，联系旧知，使“分数的基本性质”呼之欲出。

（三）迁移发散：方向多元

如果学生仅仅在教师的引导下进行完全预设的探究活动，独立性和探究味显然是不够的，为了让学生真正经历创想学习的全过程，在学生掌握基本的探究方法后，应给他们充足的时间用不同的例子進行实践、求证。

“分数的基本性质”的探究过程，除了让学生分析、比较容易观察的分数，还要让学生列举特殊分数，反向验证是否具有这样的规律。从不同的角度和方向，让学生进行独立探究、迁移发散，进一步发展合情推理、演绎推理能力，积累数学活动经验。通过之前的学习，学生初步发现：找一个相等的分数只要将分子、分母同乘一个数。这个发现实际上已经完成了分数基本性质认识的一部分。这时，需要引领学生形成一定的思维路径，为后面的学习提供思维参照。

教师设疑：是（3/4）这个分数特殊吗？还是这种方法适用于所有分数呢？让我们来试一试吧！请找出与（2/7）相等的分数，你能直接找到与它相等的分数吗？

学生找与（2/7）相等的分数，教师板书学生找到的分数，得出结语：分数的分子和分母同时乘相同的数，都可以得出相等的分数。

教师板书，如图5所示，引导学生反向观察：你能发现什么？学生不难发现“分子、分母同时除以2，分数大小也不变”，并自然迁移得到如图6所示的发散结论（可多举几个例子说明）。

教师总结完善：给你一个分数，找与它相等的分数，现在有几种方法？（两种）哪两种？（分子、分母同时乘或除以一个相同的数）这样，学生很自然地完整得出分数基本性质的结论。

（四）练习反馈：循序渐进

在通过自主建构得出分数的基本性质之后，根据认知规律，学生对知识的理解和实际运用之间还有很大的距离，还需要充分巩固和深入理解。这时，一般安排学生独立尝试解决问题，在练习反馈中暴露出学生个体理解所学知识的真实情况，以便教师相机进行个性化指导和点拨。

本节课中，教师可以提供这样一组填空题：

还可以增加难度，设置应用题：

（五）形成结构：瞻前顾后

按照创想学习“大单元”的设计原则，我们摒弃“就事论事”地教学数学知识，而将数学知识结构化、整体化。将每一个知识点放进大的知识网去看，这个知识点就可以向各个方向推演，每个知识点之间的地带学生都可以深度研究。这就鼓励学生对数学知识不断追问，不断猜想、验证，促进深度理解。

“分数的基本性质”的学习，最终也要让学生贯通与商不变的规律、分数除法的意义等之间的关系，理解分数基本性质的本质意义，为以后的约分、通分提供学习基础，并使学生更好地感知数学知识之间的联系。教师可让学生交流讨论，反思自己的学习过程，总结提炼自己的学习方法和学习体验，并清晰地向他人表述，从而真正内化所学，获得属于自己的数学学习经验。

实际操作中，以上5个环节并不是一成不变的，可以根据教学内容和学生学习情况优化调整，但层层递进地引导学生不断创想、不断解决问题的方向不变。在不断自我挑战创想的过程中，学生对数学知识的理解也愈加深刻。

*本文系江苏省教育科学“十三五”规划重点资助课题“儿童创想学习活动的开发研究”（编号：Ba/2016/02/73）的阶段性研究成果。

参考文献：

[1] R.基思·索耶.剑桥学习科学手册[M].徐晓东，译.北京：教育科学出版社，2010.

[2] 蔡日增.创新原理与方法[M].北京：高等教育出版社，2001.

[3] 怀特海.教育的目的[M].庄莲平，王立中，译注.上海：文汇出版社，2012.

[4] 孔企平，张维忠，黄荣金.数学新课程与数学学习[M].北京：高等教育出版社，2003.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。