《低起点优方式深体验》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

低起点优方式深体验

范文

马志浩

摘要：分数的意义是概念教学中较为抽象的内容。传统教学模式下，学生对于分数意义的概念掌握不理想，存在量率不分、概念局限、意识缺失等问题，其根本原因是传统教学缺少对分数内容的整体架构，缺乏整体的教学观，从而导致学生对分数意义的理解不全面、不深入、不透彻。鉴于以上问题，通过查阅资料，比较不同版本教材的教学方式，理清人教版教材中关于分数概念的教学脉络，降低学生起点，优化教学方式，为学生建构立体体验，使学习目标更贴近学生、概念建构更丰富多元、数学模型更深入内心，从而让学生学得扎实、灵活、有效。

关键词：分数;意义;优化;概念教学

一、分数的意义之教学困惑

（一）现状描述

传统的课堂教学中，“分数的意义”一课教师往往难于在课堂中引导学生突破难点，深入理解分数的意义;学生一节课下来通常感觉枯燥难懂，对于分数意义的理解仅限于表象，无法真正有效掌握其内涵;学生的課后练习，错误多种多样，需要进行反复练习。

针对上述问题，笔者进行了梳理归纳，发现对于分数的理解存在以下问题：

1.量率不分

学习“分数的意义”一课后，经常会出现这类题目，甚至到六年级学生对于这类题目也常常混淆不清。

2.概念局限

新课结束后，对于任教的一个班进行“分数的意义”概念后测。

3.意识缺失

学习分数的概念，不仅需要学生深入理解并掌握其概念，还要灵活运用概念对具体情况中的分数做出合理的分析，从而寻求有效的解题策略，显然这是对学生更高层次的要求。然而教学实践中，不管是教师还是学生运用分数的意义分析实际问题的意识都比较欠缺。

（二）归因分析

学生在学习“分数的意义”一课时存在的问题多种多样，导致学生学习困难的根本原因是什么呢？

1.量率不分→教学缺乏量率沟通

分数的认识分两个教学阶段：第一阶段是分数的初步认识（三年级），第二阶段是分数的意义（五年级）。

“分数的意义”一课在内容编排上，主要引导学生理解部分与整体、部分与部分之间的关系，此时的分数是“率”，并未涉及“量”。有关分数“量”的内容，仅出现于某些习题或练习中，并无具体内容呈现。

从教学实际来看，大多数一线教师对于涉及分数的知识缺乏系统的梳理，往往会忽视“量”“率”两者之间的内在联系。正因为教学中缺乏两者的沟通，从而学生无法全面理解分数的意义。

2.概念局限→意义理解不深刻

张奠宙教授在“分数的定义”一文中提出了分数的四种含义：份数定义、商定义、比定义、公理化定义。由于分数有多重意义，因此教学实践中，不同的教学情境指向不同的意义。尽管人教版教材在分数这一内容的编排上采用阶段渗透、逐级递进的方式帮助学生分散学习难点，还学生一个逐步建构概念的过程，但也因此割裂了分数多种定义之间的内在联系，使得分数意义教学更多的关注表象，而忽视知识的整理架构，导致意义的理解不深刻。

3.意识缺失→知识学习单一性

五年级的学生在理解抽象的分数概念时还是存在较大的困难。虽然大部分学生能熟练背诵分数的意义，但这种“流畅性”并不能为后续学习提供较为有利的知识延伸。且在分数意义的教学中，教师过于重视概念的理解，而忽视概念的应用，忽视了分数意义的问题解决，因此导致学生仅会以分数看分数，而不太具备分析具体问题中分数所表示的意义这一能力。

二、分数的意义之教材解读

（一）不同版本教材的比较与分析

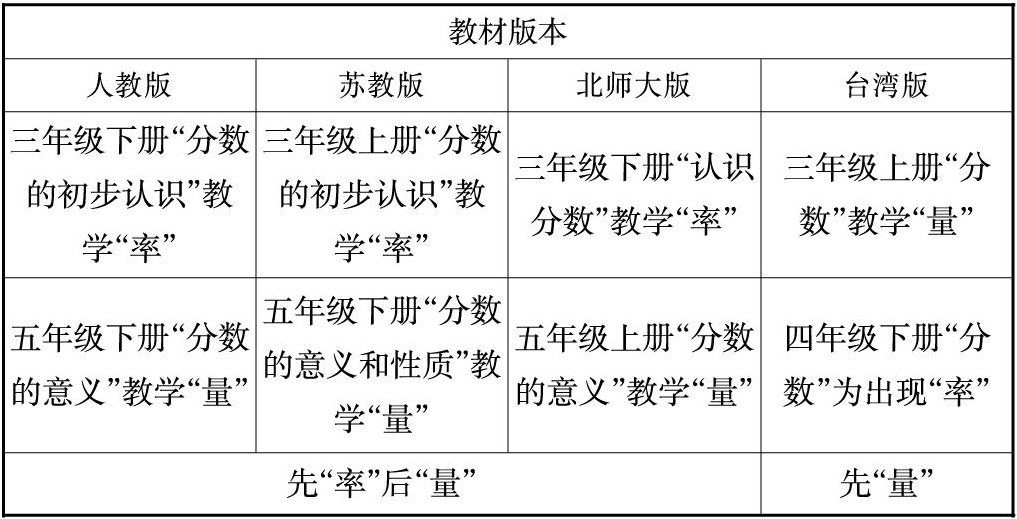
为了更好地教学分数的概念，笔者查阅了大量的教材，发现有很多版本教材的教学顺序都与现行人教版教材较为一致，先由“率”引入教学，再由“率”过渡到“量”的教学。台湾版的教材却以不同的方式开展“分数的意义”的教学，它由“量”的意义引入，在分数的大小比较、真假分数、分数与除法的关系等教学中，都是基于“量”的意义开展。

基于台湾版教材的编排，给我们的启示是分数的学习也可以是一个由“量”到“率”的过程。笔者认为，不管由“率”的教学引入“量”，还是“量”的教学引入“率”，都不可忽视分数意义中“量”“率”的联系，两者之间应相辅相成、互补内化。

（二）教材内容编排的比较与分析

人教版教材中，“分数的意义”一课的学习并非五年级开始的独立内容，早于二年级开始的平均分就为分数意义的理解打下基础，直至六年级“比的教学”也是以分数意义的理解为支撑点。因此，理清分数知识的脉络，了解分数学习的序列，读懂教材的编排才能让分数意义的理解更深入、更多元。

教材涉及的以上教学内容并非是孤立存在的，教学中不能仅以内容的教学为立足点，只要学生能将内容知识点理解即可，其他方面无须涉及过多。教材的编排是螺旋上升、不断促进、持续发展的过程，尽管每个教学阶段都有各自不同的重点，但这些内容之间彼此关联，相互补充，互相渗透，要学习好分数的意义，就要对教材有整体把握。

小学阶段分数知识的脉络：

三、分数的意义之优化教学策略

基于传统教学中遇到的问题及对学生错误原因的分析，笔者查阅资料，比较不同版本教材的教学方式，理清人教版教材中关于分数概念的教学脉络，降低学生起点，优化教学方式，为学生建构立体体验，使学习目标更贴近学生、概念建构更丰富多元、数学模型更深入内心，从而让学生学得扎实、灵活、有效。

（一）降低学习起点——让学习目标贴近学生

1.借助情境让抽象概念具体化

从上述问题可见，学生对于分数的概念属性并不清晰。传统教学模式下，学生对于分数这个抽象概念的理解难度较大，且实际运用效果并不理想。

在具体的学习情境下，可以将分数中“先分后数”的概念与归一问题建立联系。首先求出每份量，即对应分数中的分数单位;再根据每份量求出对应份数的具体量，即求出有几个这样的分数单位，得到的结果就是所求的分数。

2.借助模型使数学概念多元化

分数意义中的单位“1”既可以表示一个物体，又可以表示多个物体。传统教学中，学生受限于固有思维，仅能将单位“1”想象成一个物体或不超过份数的多个物体，然而这样的理解，对于分数概念的掌握显然是不够的。因此教学中，既要引导学生经历抽象—具体—抽象的过程，内化概念本质，拓宽概念属性，又要在逐步抽象概括中建构数学模型。

理解2：对比分析发现，不论长方形的几何直观图形数量如何变化，分数的意义只与平均分的分数及表示的分数有关，与数量多少无关。

（二）优化教学方式——让概念建构直观具体

1.埋下伏笔——指明学习方向

本课的引入从学生的已有知识出发，回顾目前为止已学习的数，引出整数、小数、分数三种概念。通过比较三类数的异同点，指向同样的数字，在不同类型的数中表示的意义不同，整数用几个几表示，小数用几个零点几或零点零几等表示，那分数可以表示成几个几分之一吗？

这样教学，引导学生感知所有的数都是由一定的单位组合而成。这无疑给予了分数单位一个新的思考方向，为后续分数单位的教学埋下伏笔。

教学片段：

师：目前为止学习过的数有？

师：他们有什么异同点？

生：都有数字3，但3表示的意思不一样。

师：真的有3个吗？

2.具体运算——构建分数意义

这里的图，有不同的层次，即：一个图形，一条线段，五个物体，十个物体。这样的设计突破了学生对于分数表示一个物体平均分的认知，为后续教学奠定了基础。接着比较四幅数量不同的图，引导学生初步感知分数的意义;再运用具体算式表示分数，并结合具体运算理解算理的过程，构建分数的意义。

师：想一想1÷5×3表示什么意思？对照图说一说每一步表示的意思。

3.对比分析——丰富概念本质

学生理解了分数意义中有关“率”的概念后，再结合具体情境，用算式表示分数的具体数量。在学生困惑同一幅图可以用两种不同的算式表示两种不同的结果时，引导学生对比两个不同的算式，从中找出异同点。在寻找异同点的过程中感悟分数意义中“量”“率”的两个概念。

将“量”的计算与“率”的计算一起呈现，不仅能通过对比分析，丰富分数意义的本质内涵，即分数既可以表示“量”的运算，也可以表示“率”的运算;还能为学生数学学习提供一种新的理念，指导今后的数学学习活动。

师：比较两个算式，想一想它们之间有什么异同点？

学生观察比较，发现：

相同点：都是÷5×3，也就是都是平均分成5份，表示其中的3份。

不同点：第一个算式用单位“1”除，除的结果是分数。

第二个算式用总数除，除的结果是具体的数量。

4.抽象概括——建构数学模型

学生对分数的意义有了深层次理解，然而，仅仅这样的学习是不深刻、不灵活的。因此，在将分数意义的抽象概念具体化后，还需将这个由抽象到具体的过程，再次抽象提升，从而内化数学知识。

上述分数意义的教学过程中，对于一个整体，我们从数学抽象的角度用单位“1”進行描述，在具体操作中用长方形的几何直观为模型进行表示。这个长方形的几何直观模型，不管赋予它多少不同的数量，其所表示的分数意义，仅与它平均分的份数及所表示的份数有关。

（三）建构立体体验——让概念学习逐级深入

1.充分体验，建构概念模型

像这样的概念教学课，很多老师以为枯燥难上，因此课堂教学中仅用十几分钟时间讲解概念，接着以大量的练习进行巩固内化。然而这样的学习，是不深刻的。事实上，概念教学中，应该给予学生充分的体验，感受概念的产生、发展及形成具体过程，从中发现规律、构建模型。

如“分数的意义”一课中，始终以长方形的几何直观为原型，教学中不断赋予长方形不同的数量与意义，引导学生感受不同数量、不同意义下长方形原型的“变”与“不变”，这样的充分体验下，概念的模型在学生脑中逐渐形成。

2.追本溯源，寻求概念本质

概念课的教学，并不以学生能熟练背诵概念为教学的立足点，且知识的掌握，也不以学生“比较好”的理解概念为落脚点。深刻理解概念、能灵活运用概念才是概念课教学的最终目标。要实现这样的目标，学生应该在课堂教学中体验概念的产生过程，在不断的对比中形成概念，再逐步分析理解概念，在抽象概括中内化概念，这样才能将概念教学落在学生心里。

如前所述，分数的本质就是“先分后数”，教学过程中，正式抓住了分数的产生过程，经历用算式表示分数、理解算理的过程，逐步构建分数的概念。

四、结语

教师在研读教材，了解学生起点时，不能只关注教材本节课的“知识点”，还要关注知识的发展脉络及相关知识之间的联系，更要关注学生对于所学知识的了解、掌握程度。教学中，我们既要抓住新旧知识之间的联系，又要立足于学生的知识生长点，建构分数意义的过程中，要打通“直观—抽象—直观”的联系，建立几何直观、具体运算与意义理解的关联，关注概念的产生、发展及形成过程，有效引导学生主动参与“建构概念”的全过程，培养学生数学建模的意识与良好的数学思维方式。

参考文献：

[1]吴正宪.小学数学教学基本概念解读[M].北京：教育科学出版社，2014.

[2]张奠宙.小学数学教学研究[M].北京：高等教育出版社，2009.

[3]张丹.小学数学教学策略[M].北京：北京师范大学出版社，2010.

[4]孔美兰.提升认识：“分数的意义”教学[J].小学数学教育，2015（6）.

[5]陈美华.分数意义理解的常见错误及教学对策[J].小学数学教育，2015（6）.

[6]张优幼.在“多元表征”中理解概念的本质：“一个数是另一个数的几倍”教学实践与思考[J].小学数学教育，2013（Z2）.

[7]肖蕾.小学数学“整数的认识”内容分析与教学研究[D].长春：东北师范大学，2013.

[8]郑毓信.概念教学中应当注意的一些问题（一）[J].小学教学设计，2014（14）.

[9]郑毓信.概念教学中应当注意的一些问题（二）[J].小学教学设计，2014（17）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。