《浅谈对高中复合函数零点问题的探究》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

浅谈对高中复合函数零点问题的探究

范文

刘俊

【摘要】复合函数的零点问题是高中阶段的数学中的一个重点和难点内容，也是高考命题中的一个热点问题，它不仅涉及了基本函数的知识内容，而且包含了丰富的数学思想的运用.本文先对复合函数的零点问题进行了简要概述，然后对复合函数零点问题的典型例题进行了剖析.

【关键词】复合函数;零点问题;求解参数

一、复合函数与零点问题

复合函数的形式是y=f[φ（x）]，其中μ=φ（x）是内层函数，y=f（μ）是外层函数.设μ=φ（x）的定义域为A，值域为B，y=f（μ）的定义域为C，值域为M，那么就有BC，且y∈M.这时，定义域A内的每一个自变量x，通过对应关系φ，都能在B中得到一个唯一确定的与之对应的μ;再通过对应关系f，就能在M中得到一个唯一确定的与之对应的y，这就确定了从A到M的一个复合关系，也就是从A到M的复合函数.

本文研究的复合函数与零点的问题，不仅与函数有关，还交汇融合了方程、不等式等知识以及数形结合、转化化归、函数与方程、分类讨论等数学思想，是一类复杂的问题.因此，数学教师要寻找便捷的解题途径，帮助学生突破学习数学的难点.以下笔者通过对典型例题的分析来探究一下复合函数零点问题中求零点个数和求参数的问题.

二、复合函数求解零点个数问题

问题“设当0≤x≤π时，函数f（x）=2sinx;当x<0时，f（x）=x2，求函数y=f[f（x）]-1的零点个数有几个.”就是一个典型的复合函数求零点个数问题，且这个复合函数的内层函数明显是一个分段函数.由于内层的函数已经确定，那么自然可以把内层函数值设为t=f（x），这样一来，就是去求函数y=f（t）-1的零点个数了.由于y=f（t）仍然满足分段函数的形式，其对应关系是确定的，因此，我们还可以利用转化思想，将问题转化为求f（t）=1中x的解的个数.在明确了思路之后，由于问题涉及的变量较多，函数形式也比较复杂，因此，可以采用数形结合的思想方法，做出函数的图像（图1），

这样去分析就会直观容易许多.由于y=f（t）的函数关系式是已知的，因此，可以求出当t的值取π6，5π6，-1时，都有f（t）=1，将t=π6，5π6，-1代入到t=f（x）的函数关系式当中，结合图1，就可以看出能取到与t=π6对应的x值有3个，与t=5π6对应的x值有1个，与t=-1对应的x值有0个，因此，函数的零点总共有4个.

通过这道经典的复合函数求零点个数问题，我们可以将这类问题的解题思路进行一个总结：① 将内层函数进行换元;② 将零点问题进行转化，一般转化为求函数y=f（t）与y=a（a为常数）的交点个数的问题;③ 解出t值;④ 数形结合通过t值找到x的解的个数.

三、复合函数已知零点个数求解参数问题

在复合函数的零点问题中，已知零点个数去求解参数也是常见的一类问题.求参数问题一直是学生觉得困难的一类问题，在结合复合函数问题之后，教师更要重视引导学生去理清思路，多渗透数学思想，帮助学生有效地掌握解题方法.

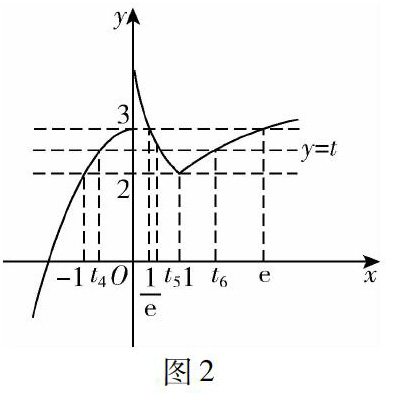
例如，问题“设当x>0时，函数f（x）=|lnx|+2;当x≤0时，f（x）=3-x2.函数y=f[f（x）]-a有5个零点，求a的取值范围.”就是一道典型的已知零点个数求参数的问题.如果学生认识到求零点个数问题的本质，那么就会发现这两类问题其实有异曲同工之妙.我们来分析这个问题，同样也需要将内层函数设为t=f（x），并将问题转化为“求函数y=f（t）与y=a（a为常数）的交点个数”或是“求满足f（t）=a的x的个数”，并要结合函数图像（图2）去分析.

从图2中可以看出，当a<2时，f（t）=a只有一个解与之对应，且这个解要满足t<-1，此时f（x）=t只有一个解，是不满足条件的.当a=2时，f（t）=a有两个解与之对应，能看出此时t的值可以取-1和1，f（x）=t就有2个解.当24时，f（t）=a有2个解，从图像上看，其中一个的取值在0，1e之间，另一个在（e，+∞）之间，前者对应的x有1个，后者对应的x有2个或者3个，最终使得原函数只有3个或4个解，因此，是不满足条件的.

以上就是对复合函数零点问题的概述与两类经典问题的分析，我们可以看到，这些问题需要较高的逻輯思维能力，因此，教师必须重视数学思想方法的渗透，让学生在有效的练习中提升求解复合函数零点问题的能力.

【参考文献】

[1]吴新建.高三微专题复习课的实践与思考——以复合函数y=f（u（x））的零点问题的教学为例[J].数学通报，2016（5）：43-45.

[2]汪正文.例谈复合函数零点问题的求解策略[J].中学数学研究（华南师范大学版），2017（1）：45-48.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。