《与动能定理有关的应用》-理学论文，物理论文-论文范文参考-科学狗论文网

标题

与动能定理有关的应用

范文

李冰

摘要：动能定理是贯穿于整个高中物理的一条脉络，它不仅能简便地处理恒力做功问题，对于变力做功问题的处理更是能化难为易。本文主要就高一力学部分的几个典型问题介绍一下如何使用动能定理，并对使用过程中容易出现的错误进行了归纳总结。

关键词：动能定理；多过程问题；变力做功；瞬间力做功；初始状态；运动过程；运动性质；运动轨迹

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）10-0047-3

动能定理的内容是高中物理的一个重中之重，是高考中必考的内容之一，并且所占的比重非常大，所以要引起我们的高度重视。动能定理连同机械能守恒定律是用能量观点解决问题的重要组成部分。动能定理的应用当然是一个关键，一次课不可能让学生一下子就能够掌握应用这个定理解决问题的全部方法，但应该教给学生最基本的分析方法，而这个最基本分析方法的形成可以根据例题来逐步让学生自己体会，笔者在教学中是通过下面几个例题循序渐进地让学生领会动能定理的解题思路，及解题的过程。

题型1 用动能定理解决匀变速直线运动问题

例1 一辆质量m，速度v0的汽车在关闭发动机后在水平地面上滑行距离L后停了下来，试求汽车受到的阻力？

解析对汽车进行受力分析可知，汽车受三个力：重力、支持力、阻力。而整个过程中只有阻力做功，而且阻力做负功。

由动能定理得：-fL=0-mv2，解得：f=。

点评这道题中，汽车的受力情况比较简单，对它的运动过程学生们掌握得也比较清楚，而用匀变速直线运动的解题方法也能解出，但是通过对比就能发现用动能定理解题的优点。

题型2 用动能定理解决多过程问题

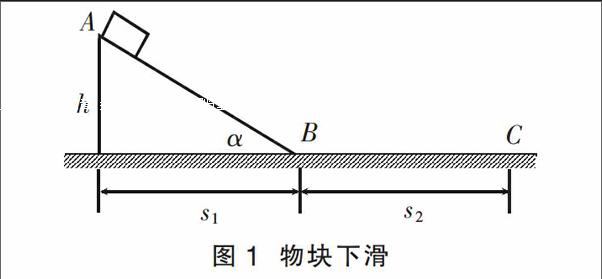
例2 如图1所示，小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h，滑块运动的整个水平距离为s，设转角B处无动能损失，斜面和水平部分与小滑块的动摩擦因数相同，求此动摩擦因数。

图1 物块下滑

解析小滑块在BC段的受力情况与上一题一样，只有摩擦力做功；而小滑块在AB段受重力、支持力、摩擦力，其中重力做正功，支持力不做功，摩擦力做负功。

分段法：

AB段：mgh-μmgcosα=mv2B-0（1）

BC段：-μmgs2=0-mv2B （2）

由（1）（2）得：mgh-μmgs1-μmgs2=0。

解得：μ==。

点评这道题是上一道题的延伸，在斜面上的受力及各个力的做功情况，学生还是比较清楚，而在水平面上的运动情况跟上一道题是一样的，所以解决起来也是比较容易。那么，多过程问题中可以用分段法和整段法。分段法用起来学生比较好理解，而整段法列起方程来就比较简单。所以我们先用分段法进行讲解，然后通过接下来的练习让学生慢慢地掌握整段法。

题型三用动能定理解决瞬间力做功问题

例3 运动员踢球的平均作用力为200 N，把一个静止的质量为1 kg的球以10 m/s的速度踢出，水平面上运动60 m后停下，则运动员对球做的功？

解析瞬间力作用的特点是作用时间短，作用力的位移也不易测量，所以我们利用功的定义是没有办法解出的。而在这个瞬间力作用的过程中，我们可以认为其他力做功为零，所以合外力做的功即这个瞬间力做的功。

由动能定理得：W=mv2-0。

解得：W=50 J。

点评这道题中，学生总是容易把60 m当作作用力的位移，这是对功的概念理解不到位。对于瞬间力做功问题，解决起来是非常简单的，但是一旦和抛体类问题联系起来，一部分同学总是会弄不清什么时间存在瞬间力，什么时间不存在。

题型四用动能定理解决变力做功问题

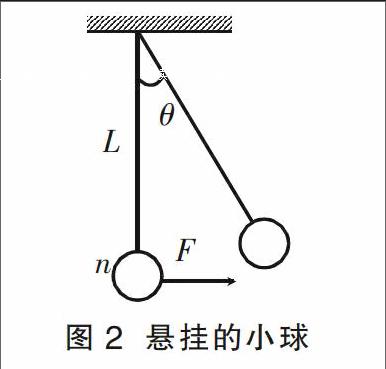
例4 如图2所示，质量为m的小球用长L的细线悬挂而静止在竖直位置。用水平拉力F缓慢地将小球拉到细线与竖直方向成θ角的位置。在此过程中，拉力F 做的功是多少？

图2 悬挂的小球

解析小球缓慢移动，时时都处于平衡状态，由平衡条件可知，F=mgtanθ。随着θ的增大，F也在增大，是一个变化的力，不能直接用功的公式求它的功，所以这道题要考虑用动能定理求解。由于物体缓慢移动，动能保持不变，由动能定理得：

-mgL（1-cosθ）+W=0，所以W=mgL（1-cosθ）。

点评利用动能定理求变力做功时，可先把变力做的功用字母W表示出来，再结合物体动能的变化进行求解。

题型五用动能定理解决与机车启动有关问题

例5 质量为m的汽车，发动机的功率恒为P，摩擦阻力恒为f，牵引力为F。汽车由静止开始，经过时间t行驶了位移s时，速度达到最大值vm，则发动机所做的功为（）

A.Pt B.fvmt

C.mv+fs D.+ E.Fs

解析汽车发动机的功率恒为P，经过时间t，根据公式W=Pt，所以A选项正确。再根据P=Fv，而当汽车达到最大速度vm时，牵引力F=f，可将公式W=Pt转化为W= fvmt，所以B选项正确。进行受力分析，汽车在竖直方所受合力为0，在水平方向只受F和f，根据动能定理，WF-fs=mv，W=fs+mv，所以C选项正确。同时也可证明D选项正确，最大速度vm=，而此时牵引力F=f。E选项不正确，因为在汽车运动的过程中，牵引力F不是恒力。

点评机车启动过程中，牵引力是变力，牵引力做的功不能用Fs来求。但是由W=Pt，可以解决恒功率启动问题，再利用机车启动中的各个量的关系解决问题。

题型六用动能定理解决与圆周运动有关问题

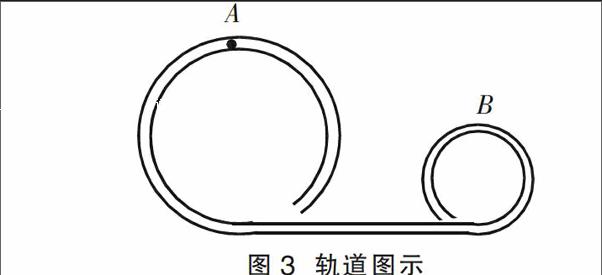
例6 如图3所示，由细管道组成的竖直轨道，其圆形部分半径分别是R和。质量为m、直径略小于管径的小球通过这段轨道时，在A点时刚好对管壁无压力，在B点时对管外侧壁压力为（A、B均为圆形轨道的最高点）。求小球由A点运动到B点的过程中摩擦力对小球做的功。

图3 轨道图示

解析由圆周运动的知识可知，小球在A点时的速度vA=。

小球在A点的动能：

EkA=mv=mgR。

设小球在B点的速度为vB，则由圆周运动的知识得：

m=mg+=mg。

因此，小球在B点的动能：EkB=mv=mgR。

小球从A点运动到B点的过程中，重力做功WG=mgR。

摩擦力做功为Wf，由动能定理得：

EkB-EkA=mgR+Wf，

由此得Wf=-mgR。

点评这类问题我们的着手点首先是受力分析，运用动能定理。然后再对竖直平面内的最高点和最低点进行讨论。内轨模型中物体通过最高点的最小速度为，双轨模型中物体通过最高点的最小速度为0。而有时又是对物体与轨道间压力有限制，那么我们就要利用合外力等于向心力来解决了。另外，如果这道题中没有摩擦力就可用机械能守恒去解决了。

参考文献：

[1]王孟宁.几个关于动能定理的综合问题[J].数理化解题研究，2006（1）：36.

[2]张占新.动能定理的几个特殊用法[J].高中数理化，2009（10）：33—34.

[3]秦付平.用动能定理巧解几类力学问题[J].中学生理科应试：高中，2009（8）：63—64.

（栏目编辑陈洁）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。