《石佛寺水库二维水动力数值模拟》-农学论文，农业论文-论文范文参考-科学狗论文网

标题

石佛寺水库二维水动力数值模拟

范文

胡艳海周林飞

摘要：石佛寺水库是辽河干流上唯一一座控制性水利工程，将其作为研究对象，基于水动力软件MIKE 21，建立了石佛寺水库二维非稳态水动力模型。利用质量平衡进行模型可靠性分析，结果表明，不合理洪水过程线是有效的，即模型是可靠的;利用2018年水库实测流量资料进行模型主要参数的率定，采用偏差统计法进行误差分析，结果表明，绝对值偏差为72 m3/s，相对误差为7.5%，模型计算误差在允许范围内，满足精度要求;实现了水库流场变化规律的模拟计算。利用所建立的模型，进行石佛寺水库水动力情况的模拟与分析，进一步验证了模型的可靠性，可为水库的日常管理、生态治理、水质改善等提供技术支持。该模型的建立为水库水质模型提供了运行载体，是水质参数运移、消散、衰减过程研究的基础。

关键词：石佛寺水库;水动力模型;数值模拟;参数;率定

中图分类号： S271文献标志码： A文章编号：1002-1302（2020）13-0265-06

收稿日期：2019-08-13

基金项目：辽宁省水利科学技术项目（编号：20170147）。

作者简介：胡艳海（1993—），男，辽宁凌源人，硕士研究生，主要从事水文学及水资源研究。E-mail：2207567047@qq.com。

通信作者：周林飞，博士，副教授，主要从事水环境研究。E-mail：zlf924@163.com。目前，在水库研究中水动力学过程发挥着重要的作用，对水体与气体、水体本身、水体与沉积物之间的能量转化、物质传输以及能量交换等一系列过程产生一定程度的影响，是水库变化规律研究的前提[1]。从20世纪80年代开始，平面二维水动力模型逐渐变得成熟，研究者不断对数值模拟的方法进行改善与革新。在大型数字计算机以及地理信息系统技术的不断快速发展过程中，平面二维水动力模型（MIKE 21 flow model），以完全圣维南方程为基本前提来求解两维水流的水力学方法，可提供有效的参数和完整的设计条件。该模型利用有限体积算法灵活完成复杂地形的处理工作，在短时间内能够反映水库的水动力流场的变化运移情况。本研究以石佛寺水库为研究背景，建立其二维非稳态水动力模型，并经过模型参数的率定和水动力模型可靠性的验证，最终得到合理可行的水库水动力模型，为进一步和水质模型的建立和耦合提供前提条件。

辽河河源位于河北省平泉县七老图山脉的光头山，该河流河源段由东辽河与西辽河2段组成，其干流主要流经河北省、内蒙古自治区、吉林省、辽宁省4个省份，流域全长和流域面积分别为1 345 km和21.9万km2。石佛寺水库根據地形分类，属于河道形平原水库，是辽河干流上唯一一座同时兼顾防洪、生态和供水三大功能的大型控制性水利工程，其中防洪是水库的最主要功能，主要体现在对下游人口、基础设施和耕地的保护，水库行政区处于辽宁省沈阳市新城子区境内，与沈阳市区相距47 km。石佛寺水库主要水利枢纽有泄洪闸、主坝和副坝。枢纽工程等级为Ⅱ等工程，永久性建筑物等级为2级，共布置泄洪闸16孔，闸孔总宽度为248.5 m。水库开工于2003年5月，完工于2005年10月，并于2009年开始进行生态蓄水。

1MIKE 21水动力计算原理

MIKE 21 flow model（FM，平面二维非稳态数学模型）凭借着其自身强大的卡片设置功能，干、湿节点和干、湿单元的设置功能，以及非常优秀的前、后处理功能，被广泛地应用于二维水动力学现象的研究中。该模型常被推荐为水库、湖泊、河流、河口和海岸水流的二维仿真模拟工具。

1.1计算原理

MIKE 21 flow model（FM）是基于三向不可压缩和雷诺（Reynolds）值分布的纳维耶斯托克斯（Navier-Stokes）方程，同时服从于静水压力的假定和布辛涅斯克（Boussinesq）假设。由于各水力要素沿垂向变化速率远不及水平方向的变化显著，因此，考虑将沿垂向积分的二维非恒定流浅水方程作为模型的控制方程。连续方程见式（1）;x、y方向的动量方程如式（2）和式（3）所示[2]。

1.2计算方法

二维水动力数值模拟的计算方法有以下3种形式：有限差分法、有限单元法和有限体积法。基于各计算方法有着较为明显的优缺点，用户全面综合的考虑计算速度、要求的计算精度以及相应的研究对象等多方面因素进行计算方法的选择和应用，本研究针对计算区域的空间离散选择有限体积法（finite volume method），将该连续统一体细分为互相不重叠的单元，单元可以是任意形状的多边形，本研究只考虑非结构化的三角形和四边形混合形式[3]。

2石佛寺水库水动力模型的建立

2.1数据收集与前处理

2.1.1数据收集模型研究区域起始于辽河干流石佛寺水库入口断面，终止于石佛寺水库出口断面，收集2个断面2017年7月1日至2017年8月31日的水位和流量数据，以及2018年8月石佛寺水库入口、出口流量数据。采用石佛寺水库电子版地形（比例尺为1 ∶5 000）作为网格建立的地形资料。

2.1.2数据前处理数据的提取：为了精确对石佛寺水库库区地表形态的描述和模型所需网格的生成，使用南方cass软件联合Auto CAD软件，对石佛寺水库地形图内部高程点进行提取，共提取8 621个高程点信息，并利用GPS获取库区水面高程点，随后利用可折叠式水深测杆在获得高程点位置测量水深值，计算得到该点库底高程，完成一个采样点高程验证，库区共布置采样点237个;利用Auto CAD对水库地形图进行边界高程点提取，并采用同样的方法使用GPS和测深杆对提取边界高程数据进行采样验证，边界共布置采样点225个，完成建模高程数据的提取工作。

数据格式转化：将所提取的高程点，采用Excel和Notepad转换成扩展名为*.xyz的格式文件，以适合于MIKE软件模型，供网格生成使用。所使用的高程点投影坐标为Beijing1954坐标，并以此坐标作为工作空间坐标和导入库区高程点数据的坐标。

2.2计算网格制作

研究区计算网格质量的好坏很大程度上决定了模型计算是否稳定。采用Beijing_1954_GK_Zone_21N投影坐标，利用MIKE ZERO网格生成器完成网格制作，计算网格共2 832个，并采用网格编辑器对网格进行优化处理。工作区选择完成后，导入已经制作好的*.xyz边界文件，进行边界命名同时对边界以200 m距离进行均匀化处理，以最大三角形面积、最小三角形角度、最大节点个数作为网格生成的控制条件，其值分别为20 000 m2、30°、150 000 个。利用Smoth mesh功能对生成的网格进行了10 000次光滑处理，并使用网格分析模块分别检查最小计算时间、最小网格角度和最小三角形边长，即严重畸形的网格，并利用网格编辑菜单反复修改使地形文件（Bathemetry）可靠，进而保证模型的稳定性和准确度[4]。地形文件是模型完成计算所需要的区域，该文件的后缀名为*.mesh，本研究将其命名为Beijing54SFS.mesh。

研究区计算网格见图1，库区二维地形见图2。

2.3模型参数设置

MIKE 21 FM二维非稳态水动力模型参数分为计算参数和物理参数2类。计算参数包括计算步长（time step interval）、计算步数（number of step）、克朗数（Courant-Friedrich Levy number）和计算精度（solution technique）等影响方程组迭代求解的有关参数;物理参数包括干湿水深（flood and dry）、涡黏系数（eddy viscosity）、底摩擦力（bed resistance）、水边界条件（boundary conditions）等。

2.3.1计算参数考虑到数据的完整性以及可用性，选择石佛寺水库入口及出口断面2017年主汛期（2017-07-01—2017-08-31）水位、流量资料，历时62 d。因此，模拟时间为2017年7月1日至2017年8月31日，模拟时段为62 d，计算步长为 10 800 s，计算步数为488步。

克朗数（Courant-Friedrich Levy number，简称CFL）是指一种能够保证模型稳定计算的关键因素，CFL值正比于水动力模块计算所需交换数据时间、反比于三角形网格的面积[5]。通过对网格反复修改并试验，来保证模型的计算稳定性，同时为确保模型的精度和准确性，采用高阶算法，最终确定水动力模块计算所需交换数据时间为0.1～30 s，CFL值為0.85。

2.3.2物理参数初始条件（initial condition）：将石佛寺水库正常运行情况下的水位作为模型运算的初始水位，即46.2 m;根据水动力模型所具有的能够在很短的时间内就能够使计算达到稳定而形成真实流速的特点，将x、y方向的初始流速条件定义为0 m/s。

边界条件（boundary condition）：水动力模型通常情况下边界条件分为陆地边界和开边界。对于开边界又被细分为上边界（进口）和下边界（出口）。在MIKE 21中一般情况下将进口断面的流量作为上边界，将出口断面的水位过程作为下边界。因此本研究将石佛寺水库入口断面2017年7月1日至2017年8月31日实测流量数据作为进口边界，将石佛寺水库出口断面2017年7月1日至2017年8月31日实测水位数据作为出口边界，并相应地将流量和水位数据制成符合MIKE软件建模要求的时间序列文件（即*.dfs0），以此作为模型运算的边界条件。

涡黏系数（eddy viscosity）：描述空间上和时间上的不确定性物理过程，在控制方程中即为相应的附加应力项。选择Smagorinsky公式的推荐值0.28作为最终的取值。

底摩擦力（bed resistance）：底摩擦力用于防止模型的计算失稳，作为模型的率定参数之一，通常情况下将以曼宁系数作为相应的输入项，且通常选取模型的缺省值作为最终的取值，即32 m1/3/s。

干湿水深（flood and dry）：干、湿动边界主要是为了避免模型计算中出现失稳问题，即当模型在水深小于干水深时对应的网格不参与计算。需要设定3个参数，干水深（drying depth）、淹没水深（flooding water depth）、湿水深（wetting depth）。本研究3个值均取模型的默认值，分别为hdry=0.005 m、hflood=0.05 m、hwet=0.1 m。

3模型验证与分析

3.1模型的水量平衡分析

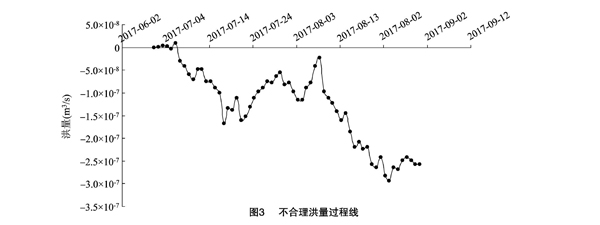
在二维水动力模型结果输出时，将文件形式设置为水量平衡。其中水流可作为该结果文件的输出项目，并且在水流项目组件下又可以包括误差（error）等项目，误差能够用于模型的可靠性分析。在进行模型可靠性分析时，通过不合理洪量过程线来诠释，即当不合理洪量过程线很低时说明模型输出结果的总水量变化符合能量守恒，也就是模型可靠性良好。所建立的研究区二维非稳态水动力模型的不合理洪量过程线见图3，仅有7月1日至7月4日误差线的值为非负，其他值均小于0，其中最小值为-3.0×10-7 m3/s，据此数据充分说明误差线是有效的，即模型是可靠的。

3.2模型的率定与误差分析

利用MIKE 21 FM水动力学模型对石佛寺水库库区进行模拟，在确定模型参数的基础上，利用2018年8月石佛寺水库入口断面的流量数据进行

计算，将出口断面模拟的流量结果输出，并使用二次摩擦定律公式τbρ0=cf·ub·|ub|，在经验值范围内调节研究区水域拖拽系数（cf）与底床流速（ub），ρ0为研究区水体密度，最终糙率值（τb）调整为0.022 2时较为合适。在MIKE 21软件中所使用的曼宁系数为糙率值τb的倒数，因此最终曼宁系数被确定为45 m1/3/s时率定效果最佳。

率定结果如图4所示，图中虚线为2018年8月出口断面流量实测值，实线为模拟值，从图中可以看出二者拟合程度良好。采用偏差统计法进行误差计算，结果表明最大绝对值偏差为72 m3/s，相对误差为7.5%，计算结果在误差允许范围内，说明模拟结果比较合理，满足精度要求，表明所构建的模型有效，可以为构建水质模型提供可靠的前提条件，进一步验证了模型的可靠性。

3.3水动力情况模拟与分析

3.3.1水深分析利用建立的石佛寺水库水动力模型输出水库水深分布，来直观表达库区水面高程分布情况。图5-a表示水库正经历重现期为300年一遇的洪水时的水深分布，图5-b表示水库恢复正常运行状态时的水深分布。无论是在洪水时段还是正常运行时段库区水深分布情况大致趋势呈现出相似的规律，在泄洪闸附近水深出现最大值、库中主槽区域水深值次之、水深在远离主槽区出现最小值，在洪水时段整个库区水深值绝大部分高于水库正常运行状态时的水深值。据此，表明模型的运行结果与实际情况一致，说明模型模拟库区水深分布趋势是正确的。在研究水体水质改善问题时，水深分布提供的库区不同分区的水深值，可为后续水质模型研究水质监测点的布置和水质参数扩散起始地点的选择提供直观的参考依据。

3.3.2流速与流态分析根据水动力模型输出石佛寺水库正常运行情况下的流速、流态分布，来表达库区流速值分布及流态变化情况，如图6、图7所示。根据流速、流态分布图可知库区主槽区域流速最显著，其平均值大致为0.60 m/s;泄洪闸区域流速值较水闸区域小些，平均流速约为 0.36 m/s;由于水生植物的局部阻碍作用，水生植物区域的水流速度最小，其平均流速约为 0.12 m/s。水动力模型提供的库区流场变化情况为污染物质的运移消散路径的初步确定提供了依据。因此，可根据石佛寺水库的流速流态，合理布置水生植物，以增加局部糙率来改变污染物质运移路径，及利用水生植物净化水质。

3.3.3瞬时流速分析输出水库正常运行情况主槽区、相对密闭区域模拟时段内的瞬时流速，如图8所示，可以看出主槽区流速明显大于相对密闭区。

瞬时流速作为影响污染物运移、扩散的主要影响因素，其大小对污染物浓度变化的影响也相当显著，具体表现为流速大时水质浓度相对较小，反之较大，因此，要注意相对密闭区的水质监测。输出水库正常运行情况下水闸位置模拟时段内的瞬时流速，将水闸位置的流速情况与实际情况相比，如图9所示，可以看出输出结果与实测结果基本吻合，进一步验证了模型的可靠性。

4结论

本研究采用MIKE 21 flow model（FM）建立石佛寺水庫二维非稳态水动力模型，通过模型稳定分析及率定，模型真实可信。利用水动力模型输出的库区模拟时段内任意时刻的各水力要素（如水深、流速、流态等）的流场分布情况，以反应各要素在水库的不同区域和不同时间段的变化关系，模型模拟结果与实测结果对比后的吻合程度表明，模拟结果可信，趋势正确，能够用于水库水情变化情况的预测，可为水库日常管理提供依据。

模型输出的库区不同分区的水深值，可为水质模型水质监测点的布置和水质参数扩散起始地点的选择提供依据;运用水库水动力模型计算获得的水流流速可为水质浓度提供水动力条件。这为进一步加载水质模型进行水库水质研究提供了基础保障。

参考文献：

[1]郭雪蕊. 基于水动力学的武汉市东湖水质模拟[D]. 西安：西安理工大学，2018.

[2]周红玉，刘操，吴晓辉. 大型跨流域调水工程对水源地水动力的影响研究[J]. 中国农村水利水电，2017（12）：104-108.

[3]李前君，杨理栋，东爱明. 防城港市渔港工程潮流数值模拟研究[J]. 中国水运，2016（11）：105-110.

[4]郑婷婷，徐明德，景胜元，等. 汾河水库水动力及水质数值模拟[J]. 水利水运工程学报，2016（3）：105-113.

[5]姜灏. 辽宁省石佛寺水库2013年汛情分析[J]. 中国防汛抗旱，2014，24（2）：72-73.彭峰生. 核桃仁脱皮机设计[J]. 江苏农业科学，2020，48（13）：271-275.doi：10.15889/j.issn.1002-1302.2020.13.054

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。