《整合教材实施主题教学》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

整合教材实施主题教学

范文

吴家全

【摘要】主题教学在数学学科并不是很理想.2017版高中新课标倡导以主题为引领的教学.学生在初中就学习了“标准差的作用”;高中统计与概率教材的各个章节也都有标准差作用的影子，但由于碎片化的分布让学生并没有形成对标准差的系统认识和理解.采用主题教学的方式设计“标准差的作用”并实施，使得教学效果比较突出，也得到了主题教学的有效策略：数学主题教学的逻辑性设计、广泛联系性实施和体验性开展.

【关键词】主题教学;标准差作用;逻辑性;联系性;体验性

主题教学可以追溯到1931 年美国芝加哥大学的莫里逊倡导的著名的“莫里逊单元教学法”，是聚焦于对某一具有重要意义的课题的理解而展开的有目的的学习体验.主题教学在语文、英语学科开展得如火如荼，但是在数学学科并不是很理想.

一、新课标对主题教学的要求

2017版的新课标中指出：教育教学要遵循教育规律和学生的身心发展规律，贴近学生的思想、学习、生活实际，充分反映学生的成长需要，促进每个学生主动发展;精选教学内容，重视以学科大概念为核心，使得课程内容结构化，以主题为引领，使得课程内容情境化，从而促进学科核心素养的落实[1].新课标数学的教学内容，是由函数等五个主题构成.新课标数学后附的案例“函数单调性主题教学设计（案例36）”为广大教师提供了主题教学的思想方法.因此，我们根据课标的精神，在数学学科的教学中，开展主题教学是很有必要的.

二、标准差在教材中的分布及学生学习状况

现以人教版教材中标准差的内容分析主题教学的必要性.初二数学人教版20.2数据的波动程度中学生学习了标准差的公式及它反应数据的离散程度的意义.高中数学人教版必修3中的2.2.2.2标准差中指出标准差是样本数据到平均数的一种平均距离，并给出了标准差的另外一种解释：居民月均用水量的100个数据落在[x--2s，x-+2s]外的只有4个，[x--2s，x-+2s]几乎包含了所有样本数据，但这种解释很多师生是没有重视的，紧接着阅读与思考中“生产过程中的质量监控图”对这种解释进行了运用，可惜绝大部分阅读材料是不会写在教材上的.高中数学人教版选修2-3中的2.3.2离散型随机变量的方差再次提到标准差刻画随机变量偏离于平均值的平均程度，大部分师生认为此知识和初中无异.高中数学人教版选修2-3的2.4正态分布中又在末尾提到了与标准差有关的3σ原则，只是正态分布要求低，教师对3σ原则一语带过.我们从教材的这些分布可以看到，教材对于标准差的编写是欲语还休，既不系统也不深刻.学生学习的关于标准差的内容最深刻的就是“标准差就是反应数据的波动性大小”.尤其，高中教材中关于标准差的知识是散乱的、没有逻辑的，因此，学生经过高中学习后对标准差的学习仍然停留在初中水平.还有，在平时的考试数据分析中，总有标准差这一栏，笔者问过教师：“标准差在分数统计时有什么用？”大部分人说没有什么用.

三、基于主题教学的标准差用途的教学设计

如何让高中阶段的学生深刻系统地认识“标准差”？笔者以“标准差的用途”为主题，整合教材，基于主题“标准差用途”进行了如下教学设计：

引入：微博中网友梆梆可爱与斯皮尔翠花的对话：“小作文500字我要写半个钟头.”“我也是.”“写完了就是一篇长文而已，没有任何浪漫或者心动的东西.”“怪不得高考语文垫底.”“我们两个文盲.”“都是人，我们的差距可能在3个标准差之外吧！”这里的“我们的差距可能在3个标准差之外”是什么意思？从而揭示主题“标准差的用途”.

问题一：下面是27人每30秒的心跳次数纪录，如何计算这组数据的标准差？

学生回忆标准差的公式

问题二：从结构上看标准差公式有什么特点？

学生计算后，对结果还是存在疑问，于是继续计算.

我们通过这两个例子，能发现：数据落在（u-2σ，u+2σ）内的频率约为95%，数据落在（u-3σ，u+3σ）内的频率约为99%.

教师及时延伸，在频率分布直方图中，组距无限小，样本无限大，得到的就是总体分布直方图，它们也符合这样的规律，如我们熟悉的正态分布也是如此.

问题三：数据落在（u-2σ，u+2σ）内的频率约为95%，数据落在（u-3σ，u+3σ）内的频率约为99%.落在区间外的数据多么？这个结论对我们有什么用？

学生思考会发现落在区间外是小概率事件.教师顺势提供案例：截至2019年9月底，印度影子银行对印度公共债券的信贷利差保持在超过5年平均水平两个标准差以上，近期外国投资者在印度公共债券中的份额从一年前的4.5%下降到2018年底的3.6%，说明越来越多的全球投资者都不再看好印度经济.

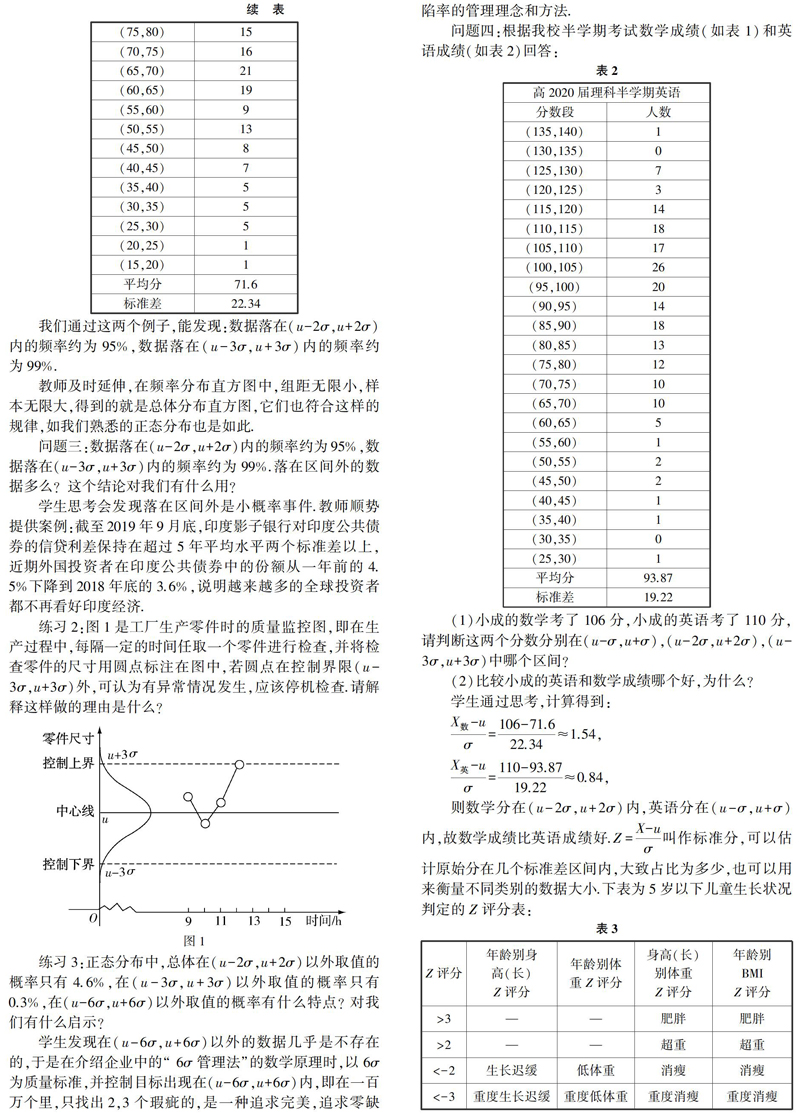
练习2：图1是工厂生产零件时的质量监控图，即在生产过程中，每隔一定的时间任取一个零件进行检查，并将检查零件的尺寸用圆点标注在图中，若圆点在控制界限（u-3σ，u+3σ）外，可认为有异常情况发生，应该停机检查.请解释这样做的理由是什么？

练习3：正态分布中，总体在（u-2σ，u+2σ）以外取值的概率只有4.6%，在（u-3σ，u+3σ）以外取值的概率只有0.3%，在（u-6σ，u+6σ）以外取值的概率有什么特点？对我们有什么启示？

學生发现在（u-6σ，u+6σ）以外的数据几乎是不存在的，于是在介绍企业中的“ 6σ管理法”的数学原理时，以6σ为质量标准，并控制目标出现在（u-6σ，u+6σ）内，即在一百万个里，只找出2，3个瑕疵的，是一种追求完美，追求零缺陷率的管理理念和方法.

问题四：根据我校半学期考试数学成绩（如表1）和英语成绩（如表2）回答：

（1）小成的数学考了106分，小成的英语考了110分，请判断这两个分数分别在（u-σ，u+σ），（u-2σ，u+2σ），（u-3σ，u+3σ）中哪个区间？

（2）比较小成的英语和数学成绩哪个好，为什么？

学生通过思考，计算得到：

则数学分在（u-2σ，u+2σ）内，英语分在（u-σ，u+σ）内，故数学成绩比英语成绩好.Z=X-uσ叫作标准分，可以估计原始分在几个标准差区间内，大致占比为多少，也可以用来衡量不同类别的数据大小.下表为5岁以下儿童生长状况判定的Z评分表：

其中自家宝宝的实测值与对应的参考宝宝群中位数之间的差值和参考宝宝群的标准差相比，所得比值为宝宝的Z评分.

标准差的用途很广泛，如有些地方的高考赋分也可以用之估计.我们在大学学习中有可能会学习到马尔可夫不等式与切比雪夫定理，它们在某种意义上刻画了标准差在反应数据离散程度的同时还刻画了每个数据偏离平均水平的程度.

四、基于主题教学的标准差用途的教学反馈

标准差这堂课设计好之后，笔者在一个中等水平的班级进行了实践，区内教师参加了这堂课的观课和议课.首先，课堂充分从标准差的定义出发，并用联系的观点让学生思考标准差的定义有什么结构特点，学生分析出标准差的定义中反应数据的偏离、平均偏离程度、保持数据的单位与之一致便于计算等情况，充分思考了数学的本源问题.其次，教师紧紧抓住主题“标准差的用途”，从标准差反应平均偏离程度角度出发，引出距离平均值一个标准差、两个标准差、三个标准差区间内的占比可能是什么，通过计算两个例子发现规律，从而把规律引申到正态分布，利用这个规律发现异常，然后，利用这个规律反过来找到数据的占比位置，从而比较不同类别数据的优越，引出标准差在标准化比较中的地位和作用.最后，教师为学生提供大学中标准差的继续研究及方向.整堂课，学生思维活跃，认识具体，课堂逻辑清晰，环环相扣.课后，笔者对学生进行了访谈，了解到学生对标准差有了全面系统的认识，并知道了标准差的三个作用及在生活中的具体应用，增加了学生对概率统计的兴趣.也有点遗憾，因标准化比较中有点仓促，学生对标准差在新高考中具体分数转化的作用还有点不够明白.

五、数学主题教学策略

主题教学由于要整合教材，创造性设计课堂，因此对教师能力要求比较高，但是它的规律也是很明显的：

（1）聚焦主题后，教师要按照知识发展逻辑和联系及设计课时顺序进行教学.教师在进行主题教学前，要能够明确与主题相关的知识的前后逻辑关系，并依据对知识的逻辑的理解和认识，进行主题教学的设计.主题的选择可以是核心概念、重要内容、数学思想、关键方法等[2].

（2）主题教学融入数学文化、生活或其他学科知识.主题教学作为一个聚焦内容，不能仅仅局限于课标、教材.为了让学生深入了解该主题内容，明确该主题的结构及学习方向，主题教学应融入数学文化、生活或其他学科知识，让学生了解主题的背景、应用及来龙去脉，为学生提供继续学习的平台和方向.

（3）主题教学体现针对性、体验性.主题教学除了要有一般课堂的规律外，它更强调针对性和体验性.主题的选择一定是经过教师精心思考并且很有必要的内容，如“疑难杂症”内容，课程灵魂内容等，同时还需要辅以课前、课后的阅读与思考、题后的反思与感悟、合理的变式、实验探究、提炼通性通法等体现学生参与主题教学的活动.

总之，主题教学是新时代教育教学多样化的一个选择.主题教学，让学生获得学习的自由，获得思想的自由，从零碎散乱的知识中解放出來，从教材的奴役中解放出来，进而获得人生的自由.

【参考文献】

[1] 崔允漷.学科核心素养呼唤大单元教学设计[J].上海教育科研.2019（4）：1.

[2]邵朝友，韩文杰，张雨强.试论以大观念为中心的单元设计：基于两种单元设计思路的考察[J].全球教育展望.2019（6）：74-83.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。