《圆形高耸结构两级变阻尼TMD风振控制》-工学论文，振动工程论文-论文范文参考-科学狗论文网

标题

圆形高耸结构两级变阻尼TMD风振控制

范文

贺辉谭平刘彦辉向越

摘要：考虑到实际工程中TMD的限位问题，提出使用两级变阻尼TMD来控制圆形高耸结构的风致振动。使用Den Hartog参数来确定TMD的频率比与第一级阻尼比。鉴于圆形高耸结构的顺风向与横风向风振效应均较为明显，推导了顺风向与横风向风荷载作用下TMD的位移响应峰值公式，以二者的较大值作为迭代依据，迭代求解TMD的第二级阻尼比。以某实际圆形高层景观塔作为工程算例进行了数值仿真分析，分析结果表明两级变阻尼TMD能有效控制圆形高耸结构风致振动，且TMD位移满足限位要求。

关键词：风致振动;圆形高耸结构;两级变阻尼;TMD

中图分类号：TU973.3+2文献标志码：A 文章编号：1004-4523（2020）03-0503-06

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.008

引言

圆形高耸结构自振周期较长、阻尼比小，顺风向与横风向风振效应都较为明显。TMD作为一种被动控制装置可以有效控制高耸结构风振响应。若根据结构设计要求去合理地选择TMD的参数，就能实现对结构风振控制。国内外众多学者对TMD参数进行了卓有成效的研究，1956年DenHartog给出了不考虑主结构阻尼的情况下TMD的最优频率比与最优阻尼比理论公式。欧进萍等结合中国风荷载规范，研究了设置TMD的高层建筑风振分析与抗风设计的实用方法。李春祥等研究了TMD-高层钢结构系统的风振舒适度控制设计方法。

在工程实践中，TMD的行程往往受到限制。腾军等对TMD的限位控制进行了研究，研究表明恰当的选择限位距离和限位阻尼系统，既能改善风致振动下结构的舒适度，又能减小TMD的摆幅。谭平等基于首次穿越破坏准则，研究了TMD在容许行程范围内不同重现期风荷载作用下的动力可靠度。文献仅涉及结构在顺风向脉动风荷载作用下的TMD限位问题，并未针对横风向风振效应较为明显的圆形高耸结构的TMD限位问题。

鉴于此，同时考虑圆形高耸结构在顺风向与横风向风荷载作用下TMD的限位问题，提出了使用两级变阻尼TMD来控制结构的风振响应。本文将从结构顺风向与横风向风振响应分析，以及两级变阻尼TMD参数设计等方面逐一展开研究。

1 结构-TMD体系顺风向风振响应

采用随机振动理论计算结构顺风向风振响应均方差，结构在脉动风脉动荷载P作用下的运动方程可表示为

式中η为保证系数，ηf（zi）为第i层脉动系数，ηz（Zi）为第i层风压高度变化系数，ηD（zi）为第i层顺风向静阻力系数，Zi表示结构第i层离地面的高度，ηr为重现期调整系数，△Ai第i层风荷载的作用面积，ω0表示基本风压。考虑各层风荷载的竖向相关性，引入相关系數

2 结构-TMD体系横风向风振响应

圆形高耸结构横风向风致振动与雷诺数密切相关，雷诺数表征了空气流动的惯性力与黏性力的相关关系，其表达式为

（1）亚临界范围：3×102e<3×105;

（2）超临界范围：3×105≤Re<3.5×106;

（3）跨临界范围：3×106≤Re。

对于圆形高耸结构而言，亚临界范围的结构横风响应较小，通常不予验算。对于超临界范围，建议按随机振动理论计算结构响应，但与跨临界范围共振相比，通常也忽略不计。因此，本文重点关注跨临界范围的圆形高耸结构横风向涡激振动。

结构第i层的雷诺数在跨临界范围内时，可将第i层横风向风荷载表示为

式中 ρ为空气密度，hi第i层层高，ωs为漩涡脱落频率，μL为升力系数。结构在横风向风荷载作用下的运动方程可表示为

3 两级变阻尼TMD参数设计

两级变阻尼TMD是将传统TMD的阻尼系数分为两个级别：当TMD位移较小时，采用第一级阻尼系数;当TMD位移超过某一特定值时，采用第二级阻尼系数。假定TMD位移限值为[δ]，TMD阻尼切换位置为[δc]，两级变阻尼TMD的工作原理简图如图1所示。图中，连接元件包括弹性刚度元件与两级变阻尼元件两部分。一般情况下，通过确定TMD的频率比与阻尼比来设计刚度元件与阻尼元件的具体参数。

可使用Den Hartog参数来确定两级变阻尼TMD的频率比与第一级阻尼比

本文将50年重现期风荷载作用下TMD的位移响应峰值作为其限位验算标准。分别求解50年重现期顺风向与横风向风荷载作用下TMD位移响应峰值Xtmaxl与Xtmax2，二者应满足

如果上式不成立，则使用迭代法求解TMD第二级阻尼比ξtopt2，迭代流程如图2所示。首先，根据预先确定的TMD质量，计算TMD质量比μ。由Den Hortog参数确定TMD频率比ropt，并初始化TMD阻尼比ξt，以式（30）作为迭代准则，迭代求解TMD第二级阻尼比ξtopt2。

以10年重现期风荷载作用下的TMD位移响应峰值Xtmax|10作为TMD阻尼切换依据。TMD位移小于Xtmax|10，采用第一级阻尼比ξtopt1。TMD位移大于等于Xtmax|10时，采用第二级阻尼比ξtopt2。

4工程算例

以某圆形高层景观塔风振控制作为工程算例，景观塔共32层，总高度为168m，28层为观光层。景观塔采用圆截面筒体结构，简体直径12m，高宽比约为14.结构所在地区地面粗糙度为B类，10年重现期基本风压为0.3kN/m2，50年重现期基本风压为0.5kN/m2。景观塔的Etabs模型如图3所示，结构基本自振周期为6.12s，结构前三阶振型如图4所示。

综合考虑结构的空间设置，TMD位移限值取0.8m。经过前期试算，决定将景观塔31层设备间安装的258t消防水箱作为TMD附加质量。

为便于分析，假定使用Den Hartog参数设计的传统TMD为TMDl，采用本文方法设计的两级变阻尼TMD为TMD2.TMD2的频率比与第一级阻尼比使用Den Hartog参数设计，使用迭代法求解TMD2的第二级阻尼比为0.21.TMD2位移小于0.54m时，采用第一级阻尼。TMD2位移大于等于0.54m时，采用第二级阻尼。

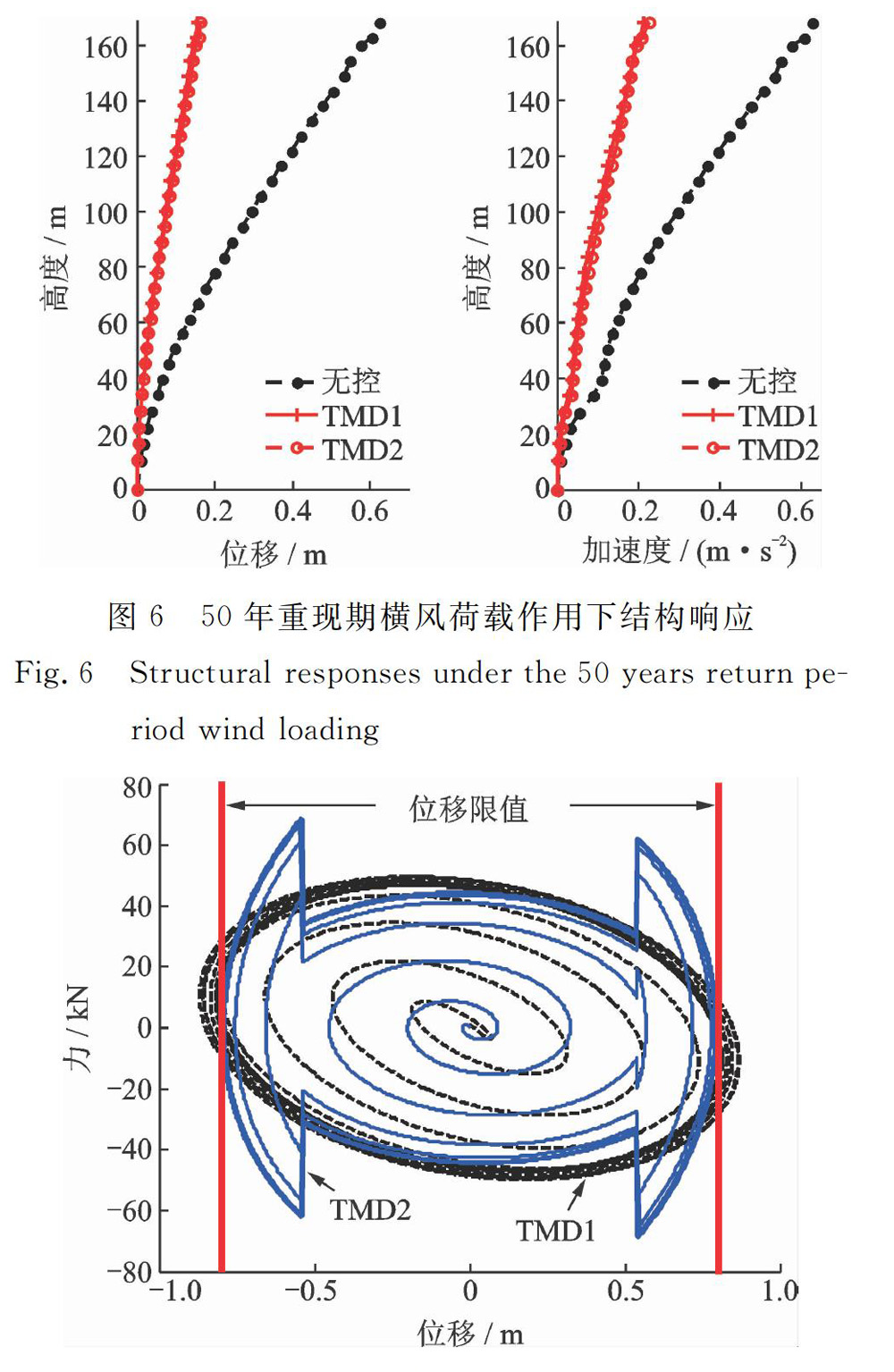
TMDl与TMD2的控制效果如图5与6所示，由图易知，TMDl与TMD2都能较好的控制结构的风振响应。10年重现期风荷载作用下TMDl与TMD2的控制效果完全相同，这是因为10年重现期風荷载作用下TMD2的阻尼并未切换。由图6可知，50年重现期横风荷载作用下TMD2与TMDl的控制效果也基本保持一致。

50年横风荷载作用下TMD阻尼元件力与位移之间的关系如图7所示，TMDl的行程大于0.8m，不满足设计要求。由于阻尼系数的切换，TMD2的行程控制在0.8m以内，满足设计要求。综上所述，TMD2能在控制效果与TMDl保持基本一致的前提下，满足限位要求。

5 结论

针对圆形高耸结构TMD风振控制开展研究，考虑到实际工程中TMD的限位问题，提出使用两级变阻尼TMD来控制结构的风振响应。以某实际圆形高层景观塔作为工程算例进行数值仿真分析，得到以下结论：

（1）提出使用两级变阻尼TMD来控制圆形高耸结构的风振响应。使用Den Hartog参数来确定TMD的频率比与第一级阻尼比，使用迭代法求解TMD第二级阻尼比。

（2）两级变阻尼TMD能有效控制结构的风振响应。

（3）对于本文算例，10年重现期风荷载作用下，两级变阻尼TMD的控制效果与传统TMD完全相同;50年重现期横风荷载作用下，两级变阻尼TMD的控制效果与传统TMD也基本保持一致，但两级变阻尼TMD能满足限位要求。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。