网站首页  词典首页

标题	2016年山东高考数学文科立体几何解法赏析
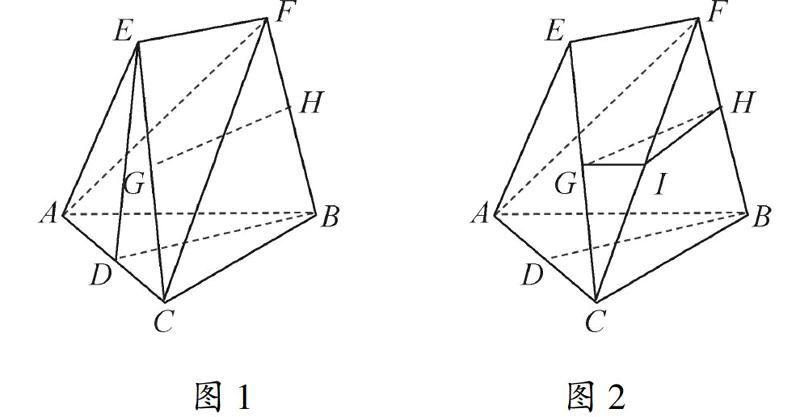
范文	王义东 立体几何既是高中数学的重点内容，又是高考的必考内容，每年高考试题中都有一道立体几何解答题，通过柱体、锥体、台体或不规则的多面体，来考查考生的空间想象能力、逻辑思维能力和运算能力.本题主要考查证明线面平行及线面垂直. 2016年山东高考文科试题 （18）（本小题满分12分） 在如图1所示的几何体中，D是AC的中点， EF∥DB. （Ⅰ）已知AB=BC，AE=EC.求证：AC⊥FB； （Ⅱ）已知G、H分别是EC和FB的中点. 求证：GH∥平面ABC. 证明（Ⅰ）因为EF∥DB，所以EF与DB确定平面BDEF. 连接DE，因为AE=EC，D为AC的中点，所以DE⊥AC. 同理可得BD⊥AC. 又BD∩DE=D，所以AC⊥平面BDEF. 因为FB平面BDEF，所以AC⊥FB. 说明：学生主要存在的问题是对线面垂直的判定不熟悉，没有说明EF与DB确定平面BDEF.另外学生出现字母的笔误较多. 典型问题：没有说明GHMN四点共面. 法五如图6，设AE，AF的中点为M、N，连接MN，NH，GN，MG∥AC，MN∥EF∥BD，面MNG∥面ABC，NG∥面ABC，NH∥AB，NH∥面ABC，面NHG∥面ABC，GH∥面ABC. 典型问题：没有说明MNHG四点共面. 思路二是通过证明线线平行，利用线面平行的判定定理进一步得到线面平行. 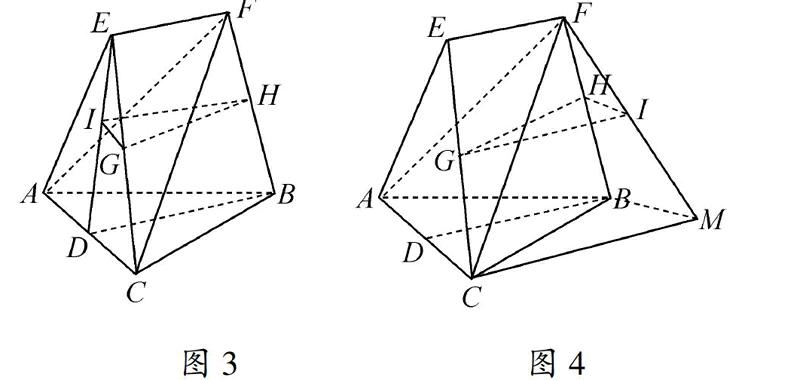典型错误：学生空间想象能力差，出现GH∥BC，GH∥BD. 总之，文科立体几何的解答题往往通过构建规则的柱体、锥体、台体和不规则的多面体，证明线线、线面、面面的平行或垂直，考查学生空间想象能力、逻辑思维能力.在立体几何解答题的解题过程中，如面面平行（或垂直）转化为线面平行（或垂直），再转化为线线平行（或垂直）；在复习中一定掌握平行或垂直的判定及性质，通过强化训练，把握解题的规律，逐步培养空间想象能力，提高逻辑思维能力，提升思维品质，只有这样，在解决问题时，才能触类旁通，举一反三.
随便看	浅析我国农村生态文明建设的长期性 防灾减灾工作的经济社会效益分析及阐述 隆化县气候变化对农业生产的影响 淳安常青村传统村落保护与利用策略研究 探析森林村庄的创建方法 梵净山自然保护区森林资源保护与社区经济协调发展的矛盾与对策分析 环北部湾地区海洋资源开发与保护的哲学思考 浅谈碳排放权交易发展与期望 关于土地财政的SWOT分析 浅析结构性理财产品面临的风险及防范措施 中小企业融资策略与融资环境优化研究 互联网金融模式下余额投资模式浅析 从网络经济学视角看互联网金融 IT视角下管理会计与财务会计的融合研究 本量利之不确定条件下的利润预测 个人证券投资风险规避策略 村级财务管理存在的问题、原因及对策 互联网时代下的财务会计发展探析 价值链管理模式下的企业财务管理探析 房地产业对我国经济的重要影响浅析 现代财务管理手段应用于高校财务管理工作的研究 农业众筹融资的发展困境与成功因素研究 我国职业教育校企合作培养实践创新人才中的困境 MOOC+课堂教学模式研究 现代职业教育中会计课程翻转课堂教学模式探析 uncoarseness uncoarsenesses uncoaxed uncoaxing uncoded uncodified uncoerced uncoercive uncoercively uncogent uncogently uncognizable uncognoscibility uncognoscible uncoincided uncoincidental uncoincidentally uncoinciding uncollapsable uncollapsed uncollapsible uncollar uncollared uncollaring uncollars 诬滥 诬漫 诬玷 诬矫 诬禄 诬秽 诬系 诬绐 诬罔 诬罔视听 诬罔诋毁 诬罪 诬胁 诬良为盗 诬艳 诬蔑 诬蔑冤枉 诬蔑善人 诬蔑毁伤 诬蔑毁谤 诬蔑诋毁 诬蔑诽谤 诬蔑，诽谤，丑化 诬蔽 诬行

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。