网站首页  词典首页

标题	意外的提问精彩的生成
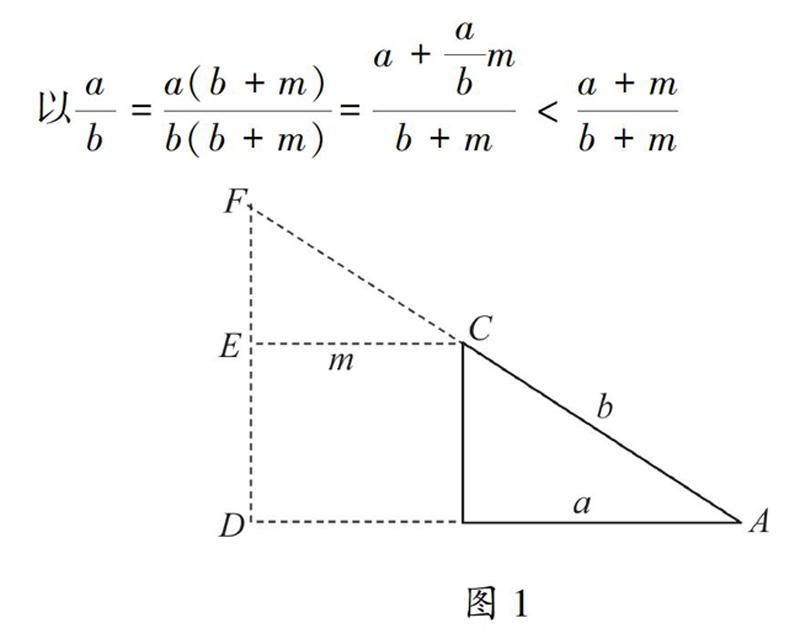
范文	王凤春 张冰 在选修教学中，为了证明不等式aba>0，m>0），我作了如下教学设计. 1教学设计 例题若水杯中的b克糖水里含有a克糖，假如再添上m克糖，糖水会变得更甜，试将这一事实用数学关系式反映出来，并证明之. 分析本例实质上是化学问题，由浓度概念可知aba>0，m>0），即糖水中加糖甜更甜. 注保和溶液时，m有取值范围. 解师生合作给出了如下证明. 证法一（比较法）a+mb+m-ab=b（a+m）-a（b+m）b（b+m）=m（b-a）b（b+m）. 因为b>a>0，m>0，所以b-a>0，b+m>0，所以m（b-a）b（b+m）>0，即a+mb+m>ab. 证法二（放缩法）因为b>a>0且m>0，所以ab=a（b+m）b（b+m）=a+abmb+m 瘙 綊 BD， 因为△ABC∽△ADF， 所以ab=a+mb+CF完成证明，师生共同给出如下推广： 设真分数a1b1则a1b1原来的教学设计是推广（*）后，讲解两道基本例题，便完成本课的教学.但是，学生甲追问（*）如何证明？这个提问既打乱了教学设计，也激发了学生的思考.课堂上片刻的沉静后，学生乙受生活模型，即上述糖水混合的启发，给出了如下证明. 2意外生成 2.1化学模型 有一种化学溶液，装在标号分别为1号，2号，…，n号的瓶中，其溶质和溶液的质量分别是（a1，b1），（a2，b2），…，（an，bn），且浓度满足a1b1若将1号，2号混合，其浓度为a1+a2b1+b2，所以有 a1b1将1号，2号，3号混合，其浓度为a1+a2+a3b1+b2+b3， 所以有a1b1依次類推，（*）式成立. 这个模型直观易懂，无需数学的逻辑推理，说出了（*）式的本质. 2.2几何模型 图2如图2，设AC1=a1，AA1=b1，A1D2=a2，A1A2=b2，A2D3=a3，A2A3=b3. 因为a1b1显然有a1b1a1b1经过一番讨论，学生甲给出这个模型，全班学生无言，同学们对他们竖起了大拇指，一种成功感溢于言表，我也为弟子们的精彩表现而自豪. 3精彩应用 学生的精彩发现，让我对学生的思维有了更高的预期，于是我改动了例题，把原本当做思考题的题目作为课堂练习. 练习（2013年北大保送生） 已知：正数a，b，c，满足a求证：a1+a证明：因为ab+c+bc1+b+c+bc>b+c1+b+c>a1+a. 应用公式，学生很快给出了上述解答.学生意犹未尽，但此时铃声已响…… 课后反思本课由于一位学生的疑问，引发了全班学生的思考.两个模型的建立，让学生产生兴奋惊奇，无字的证明，将课堂气氛推向高潮，扣人心弦.其间，老师及时捕捉学生灵光闪现的思维火花，调动学生积极参与，充分暴露学生的思维过程，才有如此大的收获.模型二实质上是对不等式链的几何解释.如何落实中学数学核心素养，设计具有挑战性的问题，深度学习，启发学生的高阶思维是个有效的途径，新课程以学生发展为本的口号喊了多年，然而，课堂教学真正体现这种理念，还需经常反思自己的教学行为.学生带着自己的知识、经验、思考、兴趣参与课堂活动，可以独立思考、个性化理解、自由表达，可以质问、怀疑、批判教师观点或教材观点，从而使课堂教学呈现出多样性、丰富性和随机性.这样的教学对教师提出了新的要求，不仅要有新的理念，还必须具有深厚的学科底蕴，才能把握课堂，使课堂教学焕发出生命活力. 作者简介王凤春（1962—），男，江苏徐州市人，上海市特级教师，上海师范大学数理学院硕士生导师.主要研究方向为中学数学教育和教育科研.出版《中学数学教育科研》等著作；解决了最优化问题中 Lagrange乘数法的相关问题，论文发表在《高等数学研究》. 张冰（1979—），女，湖北黄冈市人，中学高级教师，主要研究方向为高中数学教学和教育科研，宝山区学科带头人，宝山区教育学院高中数学兼职教研员.
随便看	加强和改进德育工作，培养合格中职人才 钢铁企业锅炉爆管的原因及处理 重构课堂教学模式以培养学生自主学习能力 《三国至隋唐的思想文化》教学设计 智慧课堂在小学美术课堂教学中的实践 闲人赵大姐 正面教育是引导学生的好方法 试谈古代人性观与教育观 增强互动，提升能力 幸福教育，开采幸福 与纸共舞 我愿为你融化一粒盐 英语专业听力课堂的跨文化交际意识培养 当“我们”同在一起 心理拓展训练在中职体育课中的运用探索 小学数学深度学习的策略指导 体验教学在小学语文作文教学中的应用 小学数学教学中学生自主学习能力的培养 生态翻译学视角下大学英语翻译教学探析 小学数学教学有效性探究 精心预设 推动“数感” 小学低年级语文教学中口语表达能力的培养 浅议幼儿行为习惯的培养 基于学科核心素养的高中英语读写结合教学研究 物理知识在高中通用技术课中的应用 prediscernment prediscernments prediscerns predischarge predischarged predischarges predischarging prediscipline predisciplined predisciplines predisciplining predisclose predisclosed prediscloses predisclosing pre-disclosure predisclosure predisclosures prediscontent prediscontented prediscontentment prediscontentments prediscontents prediscount prediscountable 庭审笔录 庭室 庭帏 庭户 庭教 庭柱裂 庭欢 庭烟 庭燎 庭燎赋 庭玉 庭砌 庭落 庭训 庭训和仪范 庭诰 庭趋 庭辩 庭長 庭闱 庭阁 庭阙 庭阶 庭阶兰玉 庭阶堂宇

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。