《矩阵运算在企业设备更新中的应用》-工学论文，工业技术论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

矩阵运算在企业设备更新中的应用

范文

唐天国

摘要：矩阵及其运算是线性代数中一个重要内容，也是现代企业和社会经济工作中处理线性经济模型重要的数学工具。本文着重研究如何根据企业、社会经济中一些零散的数据来构造矩阵并借助矩阵运算结果为企业决策提供依据。

关键词：矩阵；矩阵运算；更新设备；应用

中图分类号：O151 文献标识码：A

一、矩阵的运算

1.矩阵的加法

2.矩阵的乘法

定义2设A=（aij）mn，B=（bjk）ns，则矩阵C=（cik）ms称为矩阵A与B的乘积，记为C=AB

其中cik=ai1b1k+ai2b2k+…+ainbnk，即矩阵C的第i行k列元素为矩阵A的第i行元素与矩阵B的第k列对应元素乘积之和。

3.矩阵的数量乘法

二、矩阵运算在企业设备更新中的应用

矩阵及其运算是线性代数中一个重要内容，也是现代企业和社会经济工作中处理线性经济模型重要的数学工具。下面以一个企业的设备更新为例来探讨矩阵运算的具体应用，如何根据企业需求和数据来构造矩阵并通过矩阵运算的结果来为企业提供决策依据，已成为现代企业管理中一个重要方法。

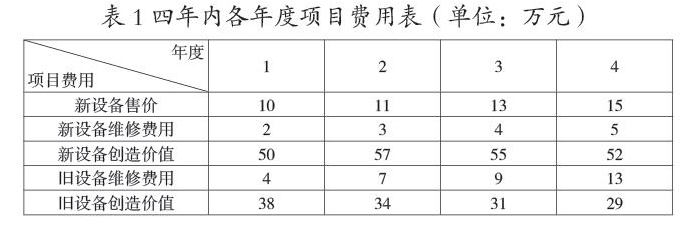
一个企业打算更新一批设备，如果购买新设备则成本太高，但创造的价值大；如果继续使用原有的旧设备，则一方面需要支出大量的维修费，另一方面创造的价值小。现假设以更新一种设备为例，期限4年，该设备在4年内的各年度售价、维修费、创造的价值见表1。现测算一下，到底在第几年更换新设备才能取得最佳经济效益（运算结果的净价值最大）。

1.构造矩阵

以4年内某年更换新设备的相关费用为行，对应的各年度相关费用为列构造如下几个矩阵：

（1）新设备维修费用矩阵

（2）旧设备维修费用矩阵

（3）新设备创造价值矩阵

（4）旧设备创造价值矩阵

上面4个矩阵的第1、2、3、4行分别表示在第1、2、3、4年度更换新设备时对应的相关费用。

（5）新设备成本矩阵

2.运算决策

（1）总维修费用矩阵

（2）总创造价值矩阵

（3）净价值矩阵

我们若将总创造价值矩阵—总维修费用矩阵—设备成本矩阵

称为净价值矩阵，用T表示，则

（4）效益矩阵

矩阵T的第1、2、3、4行分别为第1、2、3、4年度更换新设备后各年的净剩余价值，其各行之和构成的矩阵称为效益矩阵，用R表示，则

该矩阵表明，若在第1年更换新设备，则4年内净价值效益可达到190万元，第2年更换新设备则净价值效益可达到176万元，第3年更换新设备则净价值效益可达到150万元，第4年更换新设备则净价值效益只有116万元。由此可见，第1年更新设备经济效益最好，如果要求净价值不低于170万元，并考虑到提高旧设备的利用率和延长新设备的使用寿命等因素，也可在第2年更换新设备，这给企业领导层、管理者在进行设备更新前，提供了具体的预测数据，以便于他们进一步做出决策。

参与文献

[1]陈金和.经济活动中的矩阵方法[J].黄石高等专科技术学报，1995，15（4）：20-24.

[2]贺仁平.矩阵在企业经济管理中的应用[J].华东经济管理，1994（3）：57-59.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。