网站首页  词典首页

标题	搭配问题教学中折射出的新型数量关系
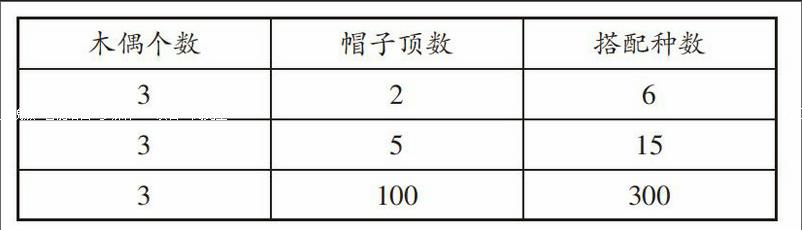
范文	郑亮 [摘 要]搭配问题涉及乘法问题，以“找规律——搭配问题”为例，简要介绍如何引导学生理解“木偶个数×帽子顶数=搭配种数”中不同单位相乘得到另一种单位的算理。搭配问题中的算理与乘法计算息息相关，厘清搭配问题中的数量关系，能促进学生更好地运用乘法来解题。 [关键词]搭配；数量；乘法；单位；算理；算法 [中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）05-0043-01 “找规律——搭配问题”是苏教版教材四年级下册的内容，教材中给出的情境是木偶搭配帽子。下面是一位教师教学本节课的一个片段。 师：儿童节快到了，妈妈让小明自选一个木偶和一顶帽子。货架上有3个不同的木偶和2顶不同的帽子。请你想一想，小明一共有多少种选择？ 生1：6种。 师：如果帽子变为5顶或100顶，又有多少种搭配方案？（依据学生的回答得到如下表格） 师：仔细观察，搭配种数与物品的数量有什么关系？ 生2：木偶个数×帽子顶数=搭配种数，也就是说搭配种数等于各类物品数量的乘积。 在巩固练习环节，教师出示题目：如果木偶和帽子共有12种搭配方法，你能据此判断木偶和帽子各有多少吗？”一位学生答道：“6+6=12……”教师忙不迭纠正：“木偶个数×帽子顶数=搭配种数，注意運算符号。”不料这位学生十分不解：“个数乘顶数，怎么等于种数啊？” 一、寻根问底，诊断病因 笔者对学生给出的“6+6=12”这一答案感到不解，难道仅仅是学生对题意理解有误吗？课后约谈才知，“6+6=12”是这位学生从“6种+6种=12种”中演化来的，于是笔者刨根问底：“按你的分析，那有多少个木偶、多少顶帽子呢？”学生回答：“可能有2个木偶、6顶帽子，也可能有6个木偶、2顶帽子。”原来这位学生会做题，只是不理解“个数×顶数=种数”这一单位转换。 学生对单位异常变换的质疑，间接暴露了教师教学上的疏漏。就教学结果来看，学生似乎根据数字关系找到了求解方法——“木偶个数×帽子顶数=搭配种数”，然而纵观整个过程，这个规律与其说是学生根据数量关系推算出来的，不如说是学生凭借直觉连估带猜出来的。实际上，学生并没有在逻辑上推理出来，因此也没有在思想上认同这一算法。 规律的总结需要大量的数据来证明，数据多、范围广，才具有说服力。因此教师还可以从配衣物、配刀叉、配新人等方面展开教学。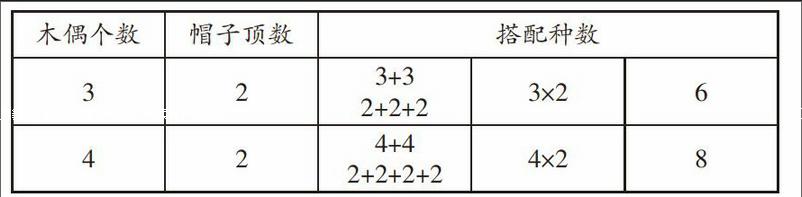 二、透过本质找规律 本课的教学重点是让学生挖掘数据背后隐藏的规律，从而找到一个通用公式，以便解决所有类似问题。但在解决个案后，教师需不需要让学生深挖其中的算理呢？答案是肯定的，因为离开算理，算法就是无本之木。以2个木偶与3顶帽子的搭配为例。如果从木偶着手，每选定1个木偶，都有3顶帽子可以与之搭配，即有3种搭配方案，由此可知，2个木偶就有6种搭配方案；如果从帽子着手，每选定1顶帽子就有2种搭配方案，那么3顶帽子就有6种搭配方案。这些都可以统一用式子“3×2=6（种）”来表示。换句话说，搭配种数的求解，需要暂定目标和机动目标协作，暂定目标和机动目标可以相互切换，而且可以互换。如把帽子设为暂定目标，那么木偶就是机动目标，两者数量的乘积就是搭配种数。 教师在教学过程中如果能够洞察算法的本质规律，阐明其中蕴含的规律，教学才会全面且深刻。在教学过程中，教师应该把算理用一种直观、简约的方式呈现出来，把抽象的规律用直观的数字符号表示出来，然后引导学生观察和探究。这样学生对“木偶个数×帽子顶数=搭配种数”的理解就会更透彻。如下表所示。 上述课例中，当“6+6=12”的错误回答出现后，教师应该耐心地让学生说出自己的想法，这样才能找到问题的根源，从而因势利导，纠正学生的思维偏差。在常规的数量关系中，每份数乘以份数等于总数，总数的单位与每份数的单位保持一致，而搭配问题的数量关系与之不同，它“脱离”了以往的算理，会让学生一时间摸不清头脑，出现思维紊乱。对此，教师只要通过实践操作让学生发现算理，就能促使学生更好地运用乘法算理来解题。 （责编 吴美玲）
随便看	利用类比教学提高中等生物理思维能力的实践探索 科学史上对天体运行的认知过程 生活物理现象在高中物理教学的融合 微元思想在高中物理中的体现及应用x 解析图象的斜率在高中物理教学中的应用 物理图象在实验“测电源电动势和内电阻”中的应用 瞬时功率与平均功率的区别 都是顺序惹的祸？ 高中物理可视化教学策略研究 浅淡体验性试验在物理教学中的运用 善待学生“错误资源” 提升物理教学效率 试论任务驱动教学法住高中物理教学中的应用 三重六环分层次物理教学法 例谈高中物理实验教学中等效思想的应用 借力创新实验 活学《电容器的电容》 高中物理课堂情境有效呈现策略的思考 追根求源寻自然 咬文嚼字学物理 牛顿运动定的知识线索与复习建议 微元思想在人教版物理教材必修一中的呈现及教学建议 例谈楞次定律中“阻碍”一词的深度解渎 例谈直流电路动态变化的归类分析 牛顿第二定律解析及应用探讨 优质高效物理课堂足怎样炼成的 开展课堂录像教学研究 提高物理教学的有效件 关于高中物理教学设计的要点研究 quicker quickest quickie quickies quickish quicklike quickly quickness' quicknesses' quicknesses quickness's quick-on-the-trigger quick ratio quickratio quicks' quicks quicksand quicksands quicksandy quick-tempered quick-trigger quick-witted quick witted quick-wittedly quick-wittedness 癞蛤蟆想吃天鹅肉 癞蛤蟆想吃天鹅肉——妄想（痴心妄想） 癞蛤蟆想吃天鹅肉——异想天开 癞蛤蟆想吃天鹅肉——痴心妄想 癞蛤蟆想天鹅肉吃 癞蛤蟆想天鹅肉吃——妄想 癞蛤蟆想飞——不是上天的料 癞蛤蟆戴草帽——装大嘴说客 癞蛤蟆打呵欠——好大的口气 癞蛤蟆打哈欠——好大的口气 癞蛤蟆打嗝儿——张口就冒坏水 癞蛤蟆打滚——腚朝天 癞蛤蟆打苍蝇——将供嘴 癞蛤蟆披鸡毛——充当漂亮鸟 癞蛤蟆挎大刀（猪八戒挎腰刀）——邋遢兵 癞蛤蟆挡车——不自量力 癞蛤蟆爬在脚面上——光唬人不咬人 癞蛤蟆爬香炉——碰一鼻子灰 癞蛤蟆生气——干鼓肚 癞蛤蟆生蝎子——一个比一个毒 癞蛤蟆生蝎子——一窝更比一窝毒 癞蛤蟆瞪眼——又想蹦达了 癞蛤蟆穿大红袍——只可远看，不能近瞧 癞蛤蟆绑在鸡腿上——飞不了你，跑不了它 癞蛤蟆装鞍子——奇（骑）怪

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。