《基于径向基函数的图像变形算法与系统研究》-工学论文，软件工程论文-论文范文参考-科学狗论文网

标题

基于径向基函数的图像变形算法与系统研究

范文

陈杰龙胡翔

摘要：图像变形技术可帮助用户获得新的图像，其广泛应用于计算机图形图像领域，具有重要研究价值。基于无网格法的图像变形采用线性混合的光滑基函数表示变形函数，往往具有天然光滑的性质，其中径向基函数是一种被广泛采用、性能良好的光滑基函数。研究径向基函数方法在不同参数下的变形行为，包括基函数采用的距离形式、采样中心个数与位置，以及径向基函数表示形式等。开发一个图像变形系统，用户可通过鼠标拖拽方式驱动图像变形，用户体验良好。实验结果表明，该变形效果光滑，且仅需2～6s即可完成变形和渲染。基于径向基函数的图像变形能获得光滑效果，且选择的参数将影响变形行为。

关键词：图像变形;无网格法;径向基函数;交互系统

DOI：10. 11907/rjdk. 201380 开放科学（资源服务）标识码（OSID）：

中图分类号：TP317.4 文献标识码：A 文章编号：1672-7800（2020）007-0227-05

Image Deformation Algorithm and System Based on Radial Basis Function

CHEN Jie-long1，HU Xiang2

（1. Fujian China Tobacco Industry Co.，Ltd.，Xiamen 361000，China;

2.School of Information， Zhejiang Sci-Tech University， Hangzhou 310018， China）

Abstract： Image deformation technology is used to help users obtain new images， and is widely used in computer graphics， and it has very important research value. The image deformation algorithms based on mesh-free method that use the linear mixed smooth basis function to express the deformation function， and they often have the feature of smoothness. The radial basis function is one kind of smooth basis functions， and it is widely used and has good properties. In this paper， we research the deformation behavior of the radial basis function method under the different parameters， including the distance form of the basis function， the number and position of the sampling centers， and the expression form of the radial basis function. In addition， in order to provide users a good interactive experience， we also develop an image deformation system which let users drive the image deformation by dragging the mouse. Experiment shows that the deformation results is smooth， and it only takes 2s ～ 6s to complete the deformation and rendering. Image deformation based on Radial Basis Function can obtain smooth deformation， and the selected parameters will affect the deformation behavior.

Key Words： image deformation; mesh-free method; radial basis function; interactive system

0 引言

圖像变形作为计算机图形学的一个重要研究方向，受到越来越多研究者的青睐与关注。基于图像变形算法，用户要想获得发生形变后的新图像，可以对原图像设置若干数量的控制点，通过改变控制点的位置使其发生变形。该技术随着理论研究与应用实践的不断深入，目前已广泛应用于形状插值[1]、图像编辑[2]、关键帧动画[3]等领域。

无网格法是图像变形中的一类重要方法，其变形函数通常采用线性混合的光滑基函数表示，使得变形具有天然光滑特性。早在20世纪90年代，Lee等[4]提出自由变形（Free-Form Deformation，FFD）方法，通过借助样条函数以实现形状变形。后来，诞生了诸如移动最小二乘法（Moving Least Squars， MLS）[5]、径向基函数法（Radial Basis Function，RBF）[6]、线性混合蒙皮法（Linear Blending Skinning，LBS）[7]等一系列经典无网格法。其中，径向基函数法（RBF）是一种很常用的无网格法。Arad等[8]较早实现了基于RBF方法的图像变形;聂烜等[9]提出一种改进的RBF变形方法，可以对多个控制点实现精确插值且变形效果平滑;韩旭里等[10]提出一种结合RBF函数的拟合方法，较好地解决了散乱数据插值和拟合不稳定问题;Levi等[11]提出一种内部RBF方法，通过保持内部球体刚性以约束形状变形，且采用测地距离作为基函数的距离形式，实现较为自然的变形。

以上方法均未针对不同参数下的径向基函数变形行为进行综合研究，这些对变形均会产生一定影响。为此，本文基于径向基函数变形方法，着重比较不同参数下的变形行为及算法性能，包括基函数采用的距离形式、采样中心个数与位置，以及径向基函数的表示形式，弥补对变形参数选择的不确定性。同时，开发一个图像变形系统，用户可通过鼠标拖拽方式驱动图像发生变形，为用户提供较好的交互式体验环境。

1 径向基函数变形算法

径向基函数（RBF）是一种光滑性较好的基函数，常用于离散数据插值技术，它在概念上很容易理解，且算法实现较为方便。每个径向基函数均具有对应的采样中心，以该中心为圆点，径向基函数对沿着半径方向的其它点呈现递增或递减变化。

为使得变形效果光滑，本文采用的变形函数由径向基函数与一次多项式的线性混合组成，即：

其中，[？（r）]表示径向基函数（[r=||u-ci||]），值域为[[0～∞]]，通常采用调和函数基，如常用的薄板样条函数：[？（r）=r2lnr]，[u]是控制点，[C={ci∈R2×1}Ni=1]是基函数采样中心点，[λi=（λ1i，λ2i）T∈R2×1]为基函数系数，即计算过程中需要求解的权值，[N]是基函数个数，[A]为[2×2]的仿射变换，[t]是平移量。

基于径向基函数的图像变形能够实现对控制点的精确插值，于是式（1）的插值条件可以表述如下：

由式（2）可以看出，该方程表示一个线性系统，需求解由权重[λk]组成的向量。于是，将式（2）表示的线性系统转化为矩形形式进行求解，令[？i，k=？（ui-ck）]，最终将该线性系统转化成如下形式：

在实际应用中，通常将控制点集[c]设置为基函数的采样中心集[p]，两者重合，即[c=p]，由此可得到[2N]个线性方程：[f（p）=q]，联合求解该[2N]的线性方程便可得到变形函数[f]。为使方程解唯一，需同时增加中心约束与正交约束：

联合求解该[2N+6]的线性方程可得到变形函数。

2 不同参数的径向基函数变形行为

徑向基函数变形能够根据不同参数改变变形行为，为用户提供更多交互控制，其变化形式主要有以下几种。

2.1 径向基函数表示形式

径向基函数由一组径向基线性组合而成，可以根据需要选择不同的表示形式（式（1）中的[？（r）]）。选择的基函数类型不同，产生的变形结果也不尽相同。几种常用径向基函数如下：①薄板样条函数：[？（r）=r2lnr];②高斯函数：[？（r）=e-r2λ2];③Multiquadric函数：[？（r）=r2+λ2];④Inverse Multiquadric函数：[？（r）=1r2+λ2]。

其中，[r]表示其它点与基函数采样中心之间的距离，[λ]为常数，需根据网格规模加以选择。

2.2 采样中心个数与位置

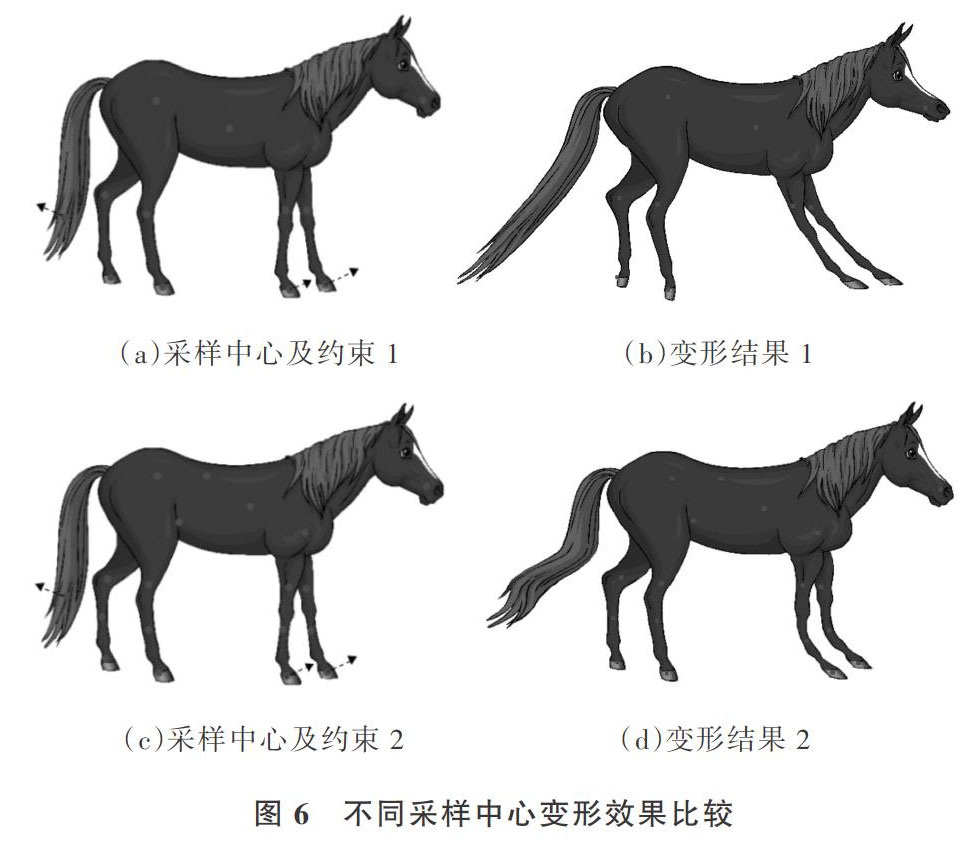
根据径向基函数影响方式，基函数采样中心个数与位置将直接影响图像变形效果。对于具有骨架结构的图像，一般将基函数中心沿着骨架方向进行采样，且采样中心之间需要有一定间距，使得采样中心在图像上均匀分布。不同采样中心个数与位置的基函数变形效果如图1所示。可以看出，若图像上的采样中心较少且散乱（见图1（a）），会导致不自然的变形效果（见图1（b）），采用均匀分布的基函数采样中心（见图1（c））则能明显改善变形效果（见图1（d）），尽可能保持图像局部形状。其中，图中的小圆点表示控制点，箭头方向表示控制点移动方向。

2.3 基函数采用的距离形式

径向基函数的影响方式与顶点距离基函数采样中心距离有关。若采用传统欧式距离作为基函数的距离度量，在求解具有骨架结构的图像时可能会造成不自然的变形结果。为此，本文引入测地距离作为基函数的距离度量。现有的测地距离求解算法有迪杰斯特拉算法、弗洛伊德算法，以及一些改进方法[12-14]。其中，由Crane等[14]提出的Heat Method（下文称热测地距离法）是一种利用热运动方程计算测地距离的方法，该方法充分利用物理学上的热扩散原理，将测地线类比于热传播线，易于理解和计算。相比其它方法，热测地距离法在计算上更为高效，且实现起来更加容易。借助带边界采样点约束的Delaunay三角化对其内部进行节点均匀分布的网格剖分[15]，根据网格的内部结构计算出测地距离。最后，将变形后的网格结构用纹理映射方式进行渲染，从而得到最终可视化效果。

使用Paraview软件对计算出的欧式距离（见图2（a））和测地距离（见图2（b））进行可视化仿真。其中，热源（基函数中心）位于深蓝色部位，用热测地距离法计算出所有顶点与该热源的测地距离，颜色的渐进表示距离长短变化，红色越深表示测地距离越长，蓝色越深表示测地距离越短。可以看出，图像中人物的两只手在欧式距离上相隔很近，但它们的测地距离则相对较远，而这取决于图像中点与点之间的位置关系（彩图扫描OSID码可见）。

3 基于径向基函数的图像变形系统

3.1 算法实现

本文算法在Intel Pentium G4600 3.6GHz双核CPU、16GB内存的笔记本上基于C++语言实现，并运行于64位版本的Visual Studio 2017开发环境下，其中借助Eigen库实现矩阵存储和运算[16]，并采用CGAL库计算网格上的测地距离[17]。

基于径向基函数的图像变形算法需根据设置的控制点和采样中心进行求解，其中采样中心个数和位置对基函数的变形行为会产生一定影响。本文利用LDLT分解法[16]求解径向基函数插值，得到权重向量;在进行测地距离计算时，利用Triangulation库[18]对形状内部进行节点均匀分布的Delaunay三角剖分，并根据标定的热源位置，计算出所有点测地距离。对图像进行基于径向基函数的变形算法步骤如下：

[3] SHEN Y，MA L，LIU H. An MLS-based cartoon deformation[J].? The Visual Computer， 2010， 26（9）： 1229-1239.

[4] LEE S Y，CHWA K Y， SHIN S Y. Image metamorphosis using snakes and free-form deformations[C].? Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques. New York： ACM Press， 1995： 439-448.

[5] SCHAEFER S，MCPHAIL T，WARREN J. Image deformation using moving least squares[J].? ACM Transactions on Graphics，2006，25（3）： 533-540.

[6] BUHMANN M D. Radial basis functions： theory and implementations[M]. Cambridge：Cambridge University Press，2003.

[7] JACOBSON A， BARAN I， POPOVIC J，et al. Bounded biharmonic weights for real-time deformation[J].? ACM Transactions on Graphics， 2011， 30（4）：78.

[8] ARAD N， DYN N， REISFELD D， et al. Image warping by radial basis functions： application to facial expressions[J].? CVGIP： Graphical Models and Image Processing， 1994， 56（2）： 161-172.

[9] 聂烜，赵荣椿，张晓燕. 一种改进的基于径向基函数图像变形方法[J]. 计算机科学，2005， 32（4）：102-103.

[10] 韩旭里，庄陈坚，刘新儒.? 基于径向基函数与B样条的散乱数据拟合方法[J]. 计算技术与自动化，2007，26（1）：65-67.

[11] LEVI Z，LEVIN D. Shape deformation via interior RBF[J]. IEEE Transactions on Visualization and Computer Graphics，2014，20（7）：1062-1075.

[12] HASSOUNA M S， FARAG A A. Multistencils fast marching methods： a highly accurate solution to the eikonal equation on cartesian domains[J].? IEEE Transactions on Pattern Analysis and Machine Intelligence， 2007，29（9）：1563-1574.

[13] RUSTAMOV R M，LIPMAN Y， FUNKHOUSER T. Interior distance using barycentric coordinates[J].? Proceedings of the Symposium on Geometry Processing （SGP）.? Eurographics， 2009.

[14] CRANE K，WEISCHEDEL C，WARDETZKY M. Geodesics in heat： a new approach to computing distance based on heat flow[J].? ACM Transactions on Graphics， 2013， 32（5）： 13-15.

[15] SHEEWCHUK J R. Triangle： engineering a 2D quality mesh generator and delaunay triangulator[C]. Heidelberg：Proceedings of Workshop on Applied Computational Geometry，1996： 203-222.

[16] GAEL G. Eigen 3.0-beta1[EB/OL].[2010-7-5].http：//eigen.tuxfamily.org.

[17] DMITRY A. CGAL 4.14[EB/OL].[2019-3-20].https：//cgal.org.

[18] JONATHAN R S. Triangle 1.6[EB/OL].[2005-7-78].http：//www.cs.cmu.edu/～quake/triangle.html.

[19] GIORGIO M. GLFW 3.0[EB/OL].[2013-6-17].https：//www.glfw.org.

[20] OMAR C. Dear-imgui 1.7[EB/OL].[2019-7-15].https：//discourse.dearimgui.org.

[21] KHRONOS GROUP. OpenGL 4.6[EB/OL].[2017-7-31].https：//www.opengl.org.

[22] BUHMANN M. A new class of radial basis functions with compact support[J]. Mathematics of Computation，2001，70（233）：307-318.

（責任编辑：孙娟）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。