《MSA在汽车冲压件质检及检验员技术评定中的应用》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

MSA在汽车冲压件质检及检验员技术评定中的应用

范文

杨天爽张新敏

摘要：测量系统的准确性会直接对产品和过程质量的判断造成影响。本文利用计数型和计量型测量系统的分析方法，以某汽车制造企业冲压车间质检工作为例，介绍了测量系统分析（MSA）的基础理论及其在冲压件质量控制中的应用过程并结合分析结果对在岗检验员技术进行评价。

Abstract： The accuracy of measurement system directly affects the judgment of product and process quality. In this paper， the basic theory of measurement system analysis （MSA） and its application in stamping panel quality control are introduced， taking the quality inspection of stamping workshop of an automotive manufacturing enterprise as an example， by using the methods of attribute and variable measurement system analysis， and the inspector technology is evaluated based on the analysis results.

关键词：测量系统分析;冲压件;Kappa;重复性和再现性

Key words： MSA;stamping panel;Kappa;GR&R

中图分类号：N37 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章编号：1006-4311（2019）13-0180-04

0 ?引言

数据的质量直接影响决策的准确性，因此测量系统分析（Measurement System Analysis， MSA）是企业质量管理的重要内容。测量系统分析是指对获取数据的测量系统能力的充足与否进行研究。在传统制造业中，主要对计数型和计量型两种测量系统进行研究，如张博等[1]对卷烟工艺测量系统进行了分析，为卷烟工艺质量的改进提供了帮助;窦智[2]利用测量系统的判定准则分析了阀体质量检测系统的有效性;Jay Arthur[3]讨论了在制造业中进行测量系统分析的重要性，探讨了设备变差和人员变差偏高的原因，并阐述了在进行测量系统分析时的常见误区;Kappele William D[4]通过降低测量系统误差，将过程能力指数从1.0提高到1.2。此外，叶卫民等[5]分析比较了测量系统分析时常采用的均值极差法和方差分析法，结合精益六西格玛改进项目进行说明，并阐述了两种方法分别适用的条件。

在汽车冲压件的制造过程中，冲压工序非常复杂，往往要经过拉延，修边，冲孔，翻边等多道工序才能得到一件成品。冲压件在成型过程中容易出现的多种表面质量问题，包括：划伤、坑、包、褶皱、颈缩甚至开裂等。汽车冲压件的质量是保证整车质量的关键，因此对冲压件表面质量要求普遍较高。

某汽车制造企业冲压车间在冲压线线尾设置多个质量检查工位，对每个冲压件的外观质量进行检查，发现不合格品则分类装箱，送至返修部门进行修复，修复合格后方可入库。同时设置SPC小组工作站，对每批次冲压件首、中、尾件不同监控点的厚度进行测量，以实现颈缩缺陷的线下监控。这就要求线尾的质量检查人员对工件的合格与否进行准确判定，SPC小组的操作员能正确使用量具对工件尺寸进行准确的测量。

不同质检人员的技术水平差异会影响判定结果和测量数据的准确性。若将不合格品判定为合格，则不合格品会流入到下序生产环节，造成更大的质量和成本损失;若将合格品判定为不合格品，则浪费大量的排查时间，影响正常生产。本文运用测量系统分析的方法对车间现阶段的计数型和计量型两种测量系统进行分析研究，并对测量系统和在岗质检人员的技术水平进行评估。

1 ?计数型测量系统

1.1 计数型测量系统的评判标准

计数型测量系统又称属性值测量系统。在很多情况下，计数型测量系统是通过人的主观对质量属性进行定性评价[6]。针对计数型测量系统，一般可从Kappa统计量、一致性比率和漏判率误判率三个方面来综合考量。

1.1.1 Kappa统计量

Kappa统计量是剔除了偶然之后的检验员内部或检验员之间的一致性，最早由Cohen在1960年提出，Fleiss等人在此基礎上也做出了杰出贡献。Cohen Kappa分析法只建立在两者比较的基础上，而Fleiss Kappa分析法则克服了这一缺陷。Fleiss Kappa分析法是将同一测量对象的所有测量结果进行两两比较，得到结果一致的次数[7]。

Kappa值的计算公式为：

其中，P0为观测一致的比率，Pe为期望一致的比率[8]。

通常，Kappa值越大，说明一致性越好。若0

1.1.2 一致性比率

一致性比率是比较多次测量之间一致性程度的统计量，计算公式为：一致性比率=（2）

一般要求测量系统整体一致性比率至少大于80%，最好达到90%，以保证测量数据准确可靠。

1.1.3 漏判率和误判率

漏判率指将不合格品判为合格品的百分率，误判率指将合格品判为不合格品的百分率。通常漏判率和误判率可接受的标准为：漏判率<5%，误判率<10%。

1.2 计数型测量系统在冲压线的应用研究

1.2.1 数据采集

随机抽取3名冲压线尾线质量检验员，编号为A、B和C。由品管人员选取15件工件（有意识地选取一些有缺陷的工件）。采集步骤：①对工件进行编号，由品管人员对工件的合格与否进行判定，以此确定工件的标准;②将工件顺序打乱，由检验员进行第1轮判定，直至3名检验员对15个工件全部完成1次判定，判定结果由记录人员记录;③所有检验员完成第1轮判定后，打乱工件顺序再实施第2轮和第3轮判定，直至所有检查员对每件工件完成3次判定为止;④将记录的判定结果进行整理。

1.2.2 测量数据结果分析与图表分析

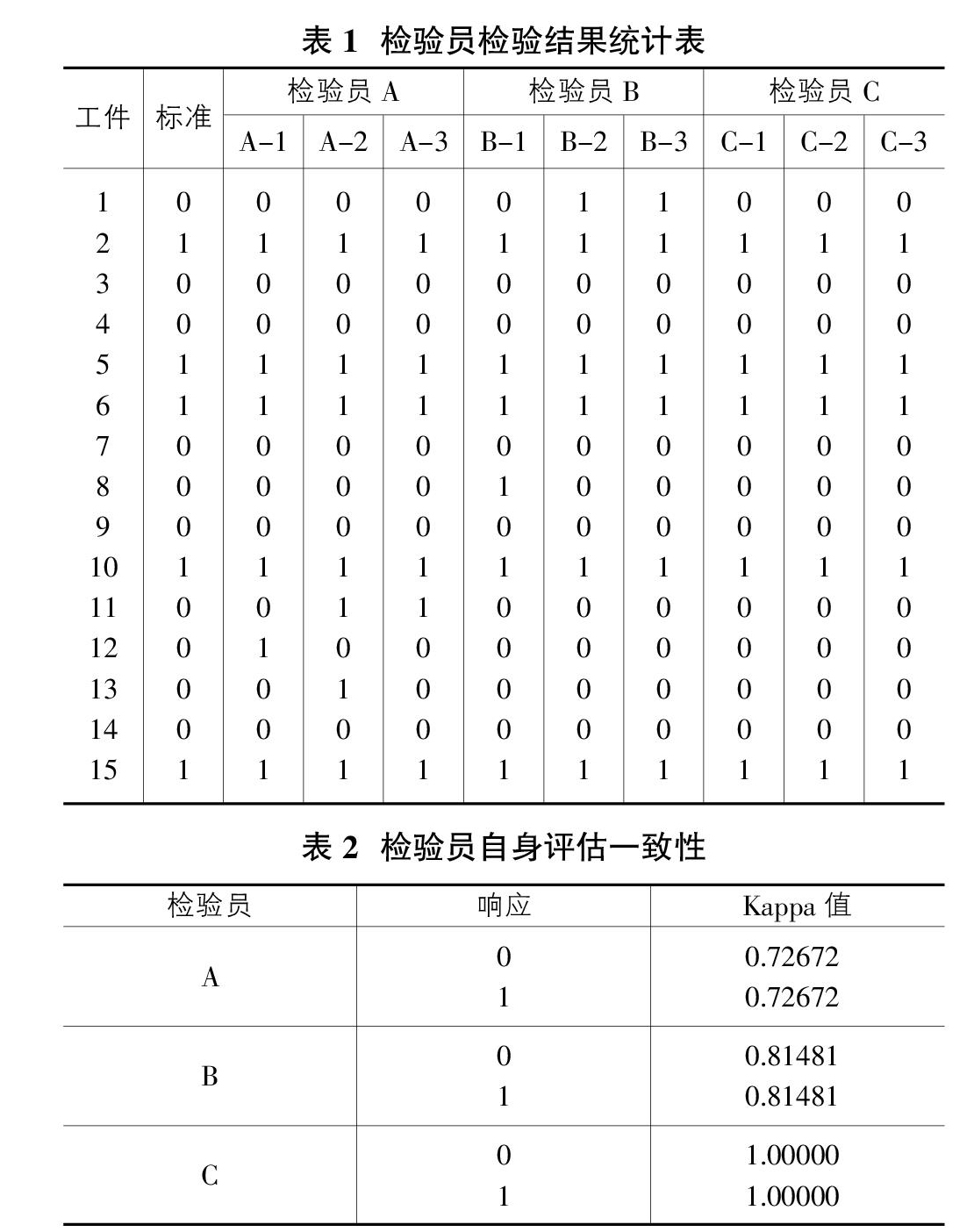
3名检验员的检验结果整理后如表1所示。其中，“1”表示合格，“0”表示不合格。

将以上测量数据导入统计分析软件中，得到如下分析结果。

①Fleiss Kappa分析结果。

由表2检验员自身评估一致性结果可知，检验员A和检验员B在每轮判定中都存在混合判定，即对某一件工件前后三次判定结果不一致，检验员A和B的自身一致性较好，但B稍优于A。检验员C对合格品和不合格品判定的Kappa值均为1.0，说明其判定结果的重复性非常好。

由表3可知，检验员A与B的Kappa值均达到0.8以上，检验员C的Kappa值为1.0，说明检验员A和B与标准的一致性非常好，检验员C的判定结果与标准完全一致。

检验员之间一致性结果如表4所示，Kappa值都达到了0.75以上，说明检验员之间的一致性非常好。所有检验员与与标准一致性的Kappa值如表5所示，都达到了0.75以上且接近0.9，说明3名检验员的判定结果与标准接近一致。

②评估一致性结果。

评估一致性图像化结果如图1和图2所示。

由结果可知，检验员自身评估一致性百分比分别是80.00%，86.67%和100.00%，检验员A、B、C的判定与标准的一致性百分比分别为80.00%，86.67%和100.00%。检验员A与检验员B与标准的一致性可以接受但略显不足，检验员C的每轮判定结果都与标准一致，可见检验员C的判定稳定且准确度高。

表6为所有检验员与标准的一致性结果，由结果可知，测量系统整体的一致性比率为66.67%，理论上一般要求该比率大于80%。

③测量系统三指标。

将评估一致性结果进行总结，并计算测量系统的漏判率与误判率，得到如表7所示的测量系统三指标。

检验员A、B、C的有效性都可接受，A和B都有提高的空间，但系统的有效性偏低。通过对漏判率的计算，发现检验员A与B的漏判率不可接受，且检验员A和B的漏判率高是测量系统有效性偏低的原因。

根据上述分析结果，检验员C的检验水平高于检验员A和B。要提高本系统的有效性需要着重降低检验员A和B的漏判率，需要加强对两名检验员的培训。

2 ?计量型测量系统

2.1 计量型测量系统的评判标准

计量型测量系统分析的目的在于分析测量系统本身的误差是否满足要求。本部分仅针对测量系统的重复性和再现性进行研究。

重复性是指评价由一个测量者，采用同一种测量仪器，多次测量同一个零件的同一特性时获得测量值的变差，又称设备变差（EV）。再现性是指评价由不同测量者，采用相同的测量仪器，测量同一零件的同一特性时测量平均值的变差，又称人员变差（AV）[9]。R&R=■称为量具的重复性与再现性的合成变差。

测量数据的波动通常为工序本身的波动？滓p和测量系统波动之？滓ms和，即■。反映测量系统能力的指标有%P/T（精度/公差比率）和%GR&R（重复性和再现性百分数）。

①测量系统的波动与被测对象公差范围的比率，记为%P/T。

②测量系统精度的估计值与过程范围的比率，记为%R&R。

若%R&R及%P/T 值皆小于10%，表示测量系统良好;若%R&R及%P/T值介于10～30%之间，表示测量系统在一定条件下可接受;若%R&R及%P/T任一值大于30%，表示测量系统不合格，必须在改进合格后方可使用。

2.2 计量型测量系统在冲压线的应用研究

2.2.1 数据采集

在数据采集时，员工用到的测量工具为数显外卡规，是专门用于测量厚度的量具，量程范围为0.00-20.00mm，测量精度为0.01mm，测量常用量程范围为0.00-1.00mm。

选择SPC小组的3名操作员A，B、C和已校準合格的数显外卡规，由质量专员选择15件待测量工件，在工件上用记号笔标记测量位置，并为每个工件编号，将样本顺序打乱。采集步骤：①三名操作员将进行3轮测量，即每人对每件待测工件都分别进行3次测量;②所有操作员完成第1轮测量后，再分别实施第2轮和第3轮测量，直至所有操作员对每一件工件完成3次测量为止;③将记录的数据整理好，进行量具R&R分析。

测量结果经整理如表8所示。

2.2.2 结果分析与图表分析

将以上测量数据导入统计分析软件中，选择方差分析法，得到表9和图2所示分析结果。

由表9可知，%GR&R=5.10%<10%，%P/T=10.92%<30%，可区分的类别数（ndc）=27>5，说明该测量系统良好，测量系统的重复性和再现性及分辨力都符合要求。

图3是测量值的量具R&R（方差分析）报告图。

（a）图的变异分量图是各变异分量大小的条形图。部件间的贡献百分比远大于量具R&R的贡献百分比，说明大多数变差来源于工件差异。

（b）图显示的是以同一个操作员同一个工件为分组变量的R控制图。R控制图表示的是三名操作员测量每个工件的最大值和最小值的差值，要求所有点应该落在控制限以内。由图示可知操作员A和B测量的重复性较好，操作员C测量的工件7和工件8超出上控制限，说明其在测量这两个工件时误差相对较大。总体上，操作员C的极差明显大于操作员A与B。

（c）图是Xbar控制图。因为所选工件涵盖了所有测量范围，所以只有在测量系统的Xbar控制图中的绝大多数平均值点（50%以上的点）落在控制限外时，該测量系统才是良好的。这与过程控制图是不同的。由图示可知Xbar控制图符合上述要求。

（d）图是工件间测量值的对比图。测量值用圆点表示，用中心有十字的圆点表示测量值的均值，将均值连接起来形成一条折线。由图示可知，每个工件的测量值分布较集中，表明操作员测量的波动较小。均值连线上下起伏波动，表明各工件均值差异明显。

（e）图是操作员对比图，是各操作员测量结果均值的连线，其变化越小，表明操作员之间差异越小。由图示可知，连线变化并不大，且操作者C的测量值稍微有些偏高。

（f）图是工件和操作员交互作用结果图，显示的是三名操作员按工件分组的测量均值的连线，分别用蓝色、红色、绿色三条连线表示。观察可知，三条线重合程度高，说明操作员与工件存在的交互作用较小，同时也可看出操作员C的大部分测量结果比操作员A和B稍高一些。

上述结果说明，现阶段该测量系统可用，但可对操作员C进行培训，提高其测量能力，并以半年为周期进行测量系统分析。

3 ?结语

冲压件的质检是冲压车间质量监控的重要环节，也是整车质量管理的重点。MSA借助数理统计为质量管理提供可靠的方法，不仅可以对当前的测量系统能力是否充足进行分析，找出影响测量系统精确性的原因，提高测量系统的检验能力，还可以对在岗检验人员的质检技术进行评价和量化分析。本文为定量评价在岗检验员技能水平提供了有效的方法，并为技能不足的质检人员指出培训方向，减少因质检人员的因素造成的结果偏差，保证测量过程处于稳定受控的状态。

参考文献：

[1]张博，张云莲，朱强，蒋志才，柴武君.测量系统分析（MSA）在卷烟工艺质量管理中的应用[J].烟草科技，2010（08）：29-33.

[2]窦智.测量系统分析在制造业中的实际应用[J].电源技术，2009，33（11）：1022-1025.

[3]Jay Arthur. Gage R&R[J]. Quality，2017，56（13）：20-21.

[4]Kappele William D. The cost of a poor measurement system： convince people of the value of measurement system analysis[J]. Quality，2017，56（7）：32-35.

[5]叶卫民，赵德勇，刘沃野，高翠娟.测量系统分析方法评述及应用[J].统计与决策，2013（02）：83-86.

[6]何桢，赵燕，邹峰.属性值测量系统分析的方法研究与应用[J].工业工程，2008（01）：82-85，121.

[7]赵越，王田田.测量系统分析在纺织品透湿性能测试判定上的应用[J].纺织报告，2017（09）：77-79，85.

[8]马逢时，周暐，刘传冰.六西格玛管理统计指南——MINITAB使用指导[M].二版.北京：中国人民大学出版社，2013.

[9]张根保，何桢，刘英.质量管理与可靠性[M].北京：中国科学技术出版社，2013.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。