《基于风险偏好的投资组合效用最大化模型研究》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

基于风险偏好的投资组合效用最大化模型研究

范文

孙多好吴芳刘刚吴晓明张玥

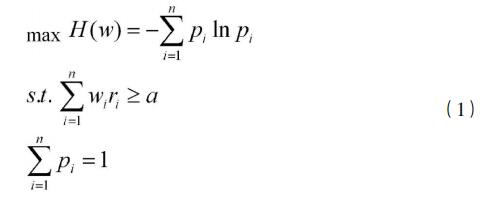
摘要：在投资过程中，风险和收益之间存在着一种权衡，这种权衡是根据投资者风险偏好的不同而不同，这就要求我们在构建投资组合时应该充分考虑投资者的风险偏好从而达到投资效用最大化。本文通过建立均值—最大熵优化模型，将风险因子引入所构建的投资组合模型中，通过调整风险因子，得到符合投资者风险偏好的投资组合，并通过汇添富消费混合基金的实证研究，验证了该投资组合效绩明显优于市场组合及样本组合。

Abstract： In the process of investment， there is a trade-off between risk and return. This trade-off varies according to investor's risk preferences， which requires that we should fully consider investor's risk preferences in the construction of portfolio so as to maximize the utility of investment.By establishing the mean-maximum entropy optimization model and introducing the risk factors into the portfolio model， this paper adjusts the risk factors to get the portfolio that meets the investor's risk preferences. The empirical study of the mixed fund of Huitian Rich Consumption verifies that the performance of the portfolio is obviously better than that of the market portfolio and sample portfolio.

关键词：风险;投资组合;均值—最大熵优化模型

Key words： risk;portfolio investment;mean-maximum entropy optimization model

中圖分类号：F830.59;F224 ? ? ? ? ? ? ? ? ? ? ? ? ? ?文献标识码：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章编号：1006-4311（2019）30-0265-04

0 ?引言

构建投资组合的目的是为了对投资风险进行分散化，从而达到既定投资收益下有效降低风险目的。因此，投资组合分散化程度就成为了投资组合效绩评价的重要指标。对于投资组合风险分散化程度量化研究，唐顺发[1]将信息熵作为基金风险分散化程度的度量指标，将风险分散化程度进行量化分析。这种方法成为继下半方差法、VaR[2]等方法之后又一被研究者关注的度量投资组合整体风险的重要方法。

本文利用信息熵构建均值—最大熵优化模型对投资组合风险分散化程度进行量化研究，得到投资组合中成分证券的权重，并引入风险因子来反映不同投资者的风险偏好[3]，从而构建出满足投资者风险偏好且效用最大化的投资组合。通过汇添富消费混合基金的实证分析，对比基于所构建的模型的投资组合与市场组合及样本组合的效绩指标夏普比、贝塔系数等，验证了基于本文所提出的模型的投资组合效绩在各个指标上都明显优于市场组合及样本组合。

1 ?模型的建立

1.1 模型的建立

1.1.1 ?主成分分析法概述

主成分分析[4]（principal component analysis）是运用降维的思想将多个自相关的指标进行处理，得到若干携带原始变量绝大多数信息且线性无关的主成分，解决了原数据指标之间的信息冗余和自相关问题。本文通过运用主成分分析对样本基金投资组合的相关指标进行降维处理，获得消除信息冗余的不相关成分。

1.1.2 均值—最大熵优化模型

投资组合的第i（i=1，2，…，n）成分证券收益率ri受各种因素的影响而发生波动，导致对应的投资权重wi会随之改变。将二者视为随机变量，由最大熵原理[5]得到投资组合分散化程度的决策模型为：

（1）

其中H（w）是熵函数，pi为风险比例，a为最低预期收益。

为了权衡分散化程度和收益率之间的关系，以满足不同风险偏好投资者的投资习惯要求，将Markowitz的均值—方差模型与均值—最大熵模型结合，建立收益率均值—最大熵优化模型：

（2）

其中Z（w）考虑风险偏好的投资组合的期望收益，θ∈[0，1]为风险厌恶系数，且θ的不同取值反映了不同投资者的风险偏好。可以很清楚的看出该模型当θ=0时为均值—最大熵模型，在θ=1时该模型变为均值—方差模型。

1.2 相关指标的选取

1.2.1 市场无风险收益率的确定

无风险利率是指在市场是能够在不承担任何损失风险的情况下所获得的收益。而在市场是任何企业和个人所发行的证券都不能保证能够只赚不赔。而银行作为国家信用的代表，有着国家的支持，可以认为其所给出的存款收益是无风险的。由于银行为了吸储而采用同一时段不同的利率且不同时段不同利率，因此本文选取了较为固定的中国人民银行一年期定期存款利率作为本文无风险收益率。由于上文中所选取的数据时间区间里的定期一年存款利率没有变，故给下文的分析带来了便利。

1.2.2 市场基准组合的确定

我国现阶段的开放式基金主要是投资于上海证券交易市场和深圳证券交易市场，而沪深300股票指数的成分股包含了在这两个交易市场上绝大多数的优质、主流股票。因此，沪深300指数就成为了两市的晴雨表和风向标，在大多数的投资组合和基金业绩评价标准中得到了广泛地运用。但是如果只用这一个指数作为评价标准，容易造成偏差，所以本文选用了上证指数和沪深300指数来构建基金业绩评价体系的基准组合，得到市场基准组合周平均收益率Rs：

（3）

其中，Rh和Rg分别表示沪深300指数和上证指数的周平均收益率。

1.3 风险指标的确定

本文主要通过均值、贝塔系数、夏普比率来反映相关投资组合的效绩。

1.3.1 贝塔系数[6]β：

（4）

其中R为所构建投资组合收益率，RM为基准组合收益率，σM为基准组合的方差，对于基准组合（市场组合）M来说其β值为1。

该指标能够表示所构建的投资组合相对于市场投资组合的收益率波动性，对于基准组合来说，它的贝塔系数为1，即相对于自身而言，基准组合是没用波动的。而样本组合的贝塔系数则一般大于0小于1，这表示相对于基准组合来说样本组合及优化组合收益率波动性的大小。贝塔值越大，说明波动性越大，风险越大;贝塔值越小，风险越小。

1.3.2 夏普比率（SharpRatio）[7]：

夏普比由夏普在Markowitz资本资产定价模型的基础上，研究资本市场线的前提下提出的。当市场处于均衡时，资本资产定价模型中的资本预期收益可由如下公式表示：

（5）

式中E（Rp）为投资组合预期收益率;rf为市场无风险收益率;E（RM）为市场基准组合预期收益率;σM为市场基准组合的标准差，其表示市场基准组合总体风险的度量;σp为投资组合预期收益率标准差。

（6）

其表示，投资组合每承受一单位总风险，会产生多少的超额报酬。举例而言，假如国债的回报是3%，而既定投资组合的预期回报是15%，投资组合的标准差为6%，则夏普比率为2，这表示投资者的风险每增加一个单位换来的是2%的多余收益。

2 ?实证分析

2.1 数据的选取

我们利用汇添富消费混合基金10只重仓股（表1）2018年6月22日到2019年5月17日，共计46周的周收益率（源于同花顺软件）验证模型的有效性。

2.2 模型运用

首先对所选取的基金重仓股2018年6月22日到11月30日这23周的周收益率进行主成分分析，得到特征值及每一成分的风险比例，再利用均值—最大熵优化模型找到符合最优化条件的投资权重wi（i=1，2，…，10）。主成分分析结果如表2。

从表2我们可以得到，十个指标对应的特征值（左边第二列），从上到下依次递减。进而可以获得每个指标不考虑风险偏好的风险比例（图1）。

下面在考虑风险偏好的情形下，针对三种风险厌恶系数取值情况讨论各个成分证券的风险分散化程度的分布情况（以下图中的成分证券是按照投資权重递减的顺序排列的）：

当θ=0时，均值—最大熵优化模型就会变成均值—最大熵模型。得到各个成分证券风险比率的分布，风险比例分布情况如图1。

从图1可以看出，在最大熵投资组合模型下各成分证券分散化几乎呈均匀分布，各成分证券风险比例相近，这说明了每个成分证券能够所携带的风险近乎相等，对于它们的分散化程度也是几乎一致的。

当θ=1时，该模型就转化Markowitz的均值—方差投资组合模型。该模型表示：在能够承受的最大风险的情况下，获得尽可能大的收益。与上面的方法相同，对收益率协方差矩阵作主成分分析，求出特征值和对应特征向量，得到风险比率分布情况如图2。

该图显示，在θ=1时，虽然风险比例集中在第一主成分上，但其余成分所携带的风险近乎相等，这说明资产之间的相关性也依然存在。而这种相关性与风险有直接关系，相关性越大，风险越大。

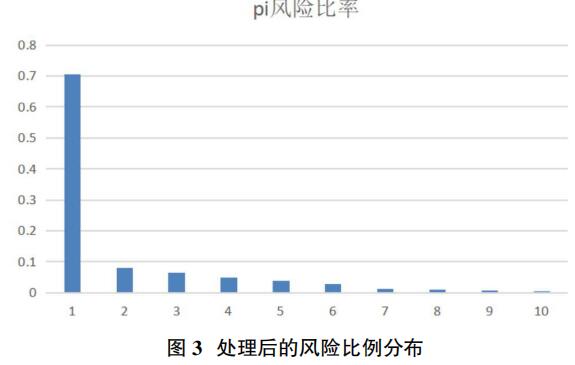
在对第一周期收益率进行主成分分析的基础上，通过优化模型得到θ=0.56时，目标函数Z（w）取得最大值，同时其风险比率如图3所示。

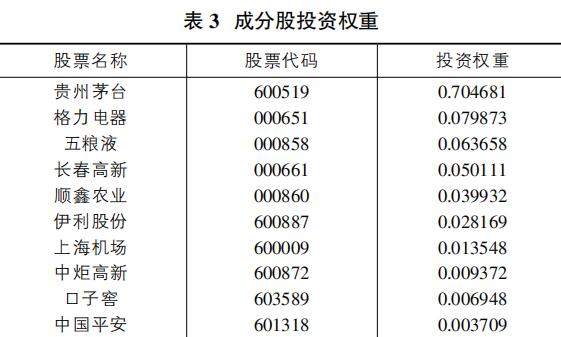
从图中我们可以看到，从第一到第十成分证券的风险比例在递减，且第一主成分所包含信息量最多。基金组合各资产权重如表3所示。

由表3可看出，第一周期期的十大重仓股投资权重由大到小分别为：贵州茅台、格力电器、五粮液、长春高新、顺鑫农业、伊利股份、上海机场、中炬高新、口子窖、中国平安。

为了能够反映出优化组合的效绩情况，我们将三种组合的收益、夏普比、方差这三个指标进行了对比（表4），可以看出优化模型的优势。

从表4中可以得知，市场标准组合的夏普比和平均收益率明显要高于样本组合;而优化组合的这两个指标又低于样本组合，这说明优化组合效绩要好于市场标准组合。

再对2018年12月7日到2019年5月17日这23周第二周期的各成分证券收益率进行主成分分析和均值—最大熵优化，得到当θ=0.68时期望收益Z（w）取得最大值，得到基金组合各成分证券的权重（表5）。

样本基金组合、优化基金组合和市场基准组合的收益率与风险特征如表6所示。

表6明显地反映出，优化基金组合的期望收益和夏普比仍明显高于其他两种组合，但其收益率波动低于其他两种组合，从而说明优化模型在一定程度上能够减小投资风险。

2.3 总结

本文选取了汇添富消费混合基金从2018年6月22日到2019年5月17日共计46周两个周期的周收益率进行实证分析。先通过主成分分析法将所选基金成分证券的每个周期的周收益率进行处理，消除指标之间的信息杂冗，然后再利用均值—最大熵优化模型得到基金的优化投资组合。最后将优化投资组合与样本基金投资组合以及市场组合的三个风险指标—方差、夏普比、贝塔系数进行对比得到如下结论：①从方差来看，通过优化模型处理而构建的投资组合方差要小于市场组合，说明优化模型能够将投资组合的非系统性风险有效的分散，且比市场组合的分散效果更好。②从夏普比率来看，优化组合具有最高的夏普比率，这说明优化组合的超额收益较市场组合及样本组合的收益高。③从贝塔系数来看，优化组合的贝塔系数也明显小于市场组合的贝塔系数，说明优化模型的收益率波动性较小，收益稳定，风险较其他两个组合小。④从优化投资组合来看，在十只股中投资比重前三依次为贵州茅台、格力电器及五粮液。

参考文献：

[1]唐顺发.基于主成分分析的我国开放式基金风险分散优化应用研究[D].华东交通大学，2018.

[2]连天一.基于VaR方法的证券投资基金风险管理研究[D].辽宁大学，2011.

[3]胡凯，朱泽钢.前景理论与开放式基金风险调整研究[J].甘肃理论学刊，2012（04）：123-128，2.

[4]A. C. Ruiz-Fernández， F. Páez-Osuna， C. Hillaire-Marcel， M. Soto-Jiménez， B. Ghaleb. Principal Component Analysis Applied to the Assessment of Metal Pollution from Urban Wasters in the Culiacán River Estuary [J]. Bulletin of Environmental Contamination and Toxicology， 2001，67（05）：741-748.

[5]曾晓华，袁持平.基于最大熵原理的金融系统风险测度及实证研究[J].东莞理工学院学报，2019（03）：94-98，124.

[6]郭范勇，潘和平.财务因素、市场因素与股票贝塔系数[J].财会通讯，2017（12）：125-128.

[7]H. Jiro. Stock performance by utility indifference pricing and the Sharpe ratio [J].Quantitative Finance， 2019， 19（2）：327-338.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。