网站首页  词典首页

标题	三角形中三条高共点问题
范文	罗秋佳 [摘 要] 证明三线共点的问题很有难度，尤其是证明三角形三条高共点，教材因为其难度大而删除了. 笔者探索把这样的问题设计成开放性问题，启发学生一步一步地探究，分析透彻图形的内在特性，最后比较严谨地证出任意三角形的三条高共点. [关键词] 三角形的高；开放性问题；探究 许多传统经典问题在培养学生的数学能力和良好思维品质上有很好的价值和作用，但因为比较繁难，所以新课程把它们删减掉了. 笔者思考，是否可以把它们重新构思成低起点、开放性的、探究性的问题，引导学生逐步探索，即把学生的思维慢慢带入其中，使学生最后能顺利地证明它呢？笔者选取了三角形三条高共点的问题，把它设计成入口宽、起点低的开放性问题，引导学生一步一步地加深思考，最后证出三角形的三条高共点. 下面先从锐角三角形再到钝角三角形的三条高必相交于一点，介绍自己的思考和做法. 透彻分析图形的内在关系，为 证明三角形三条高共点作准备 1. 把问题构思为一个低起点问题 笔者鼓励学生思考比较简单的问题：一个锐角三角形的两条高相交，那么图中有相似三角形吗？可以找到几对相似三角形？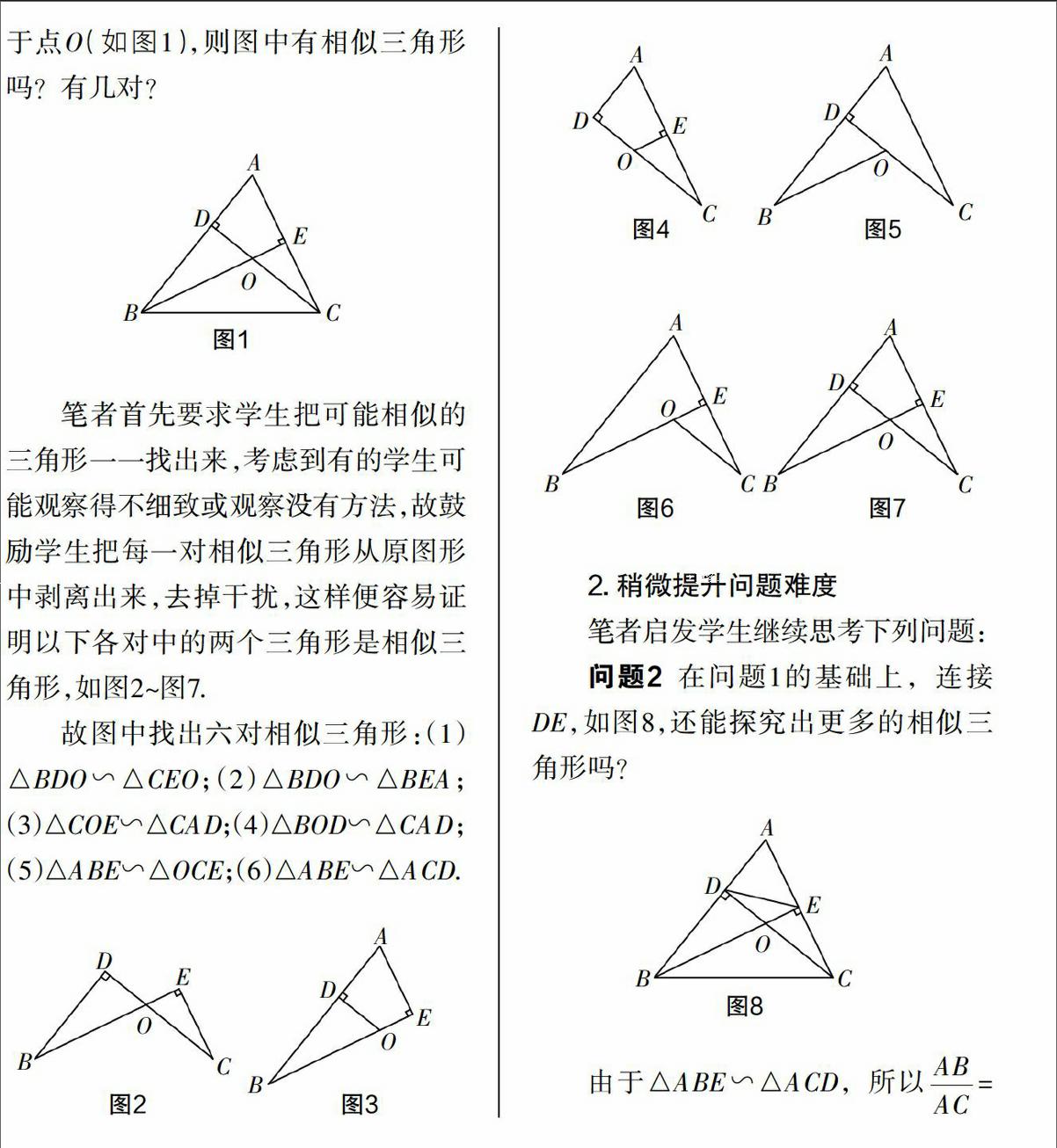 问题1？摇 在锐角三角形ABC中，BE⊥AC于点E， CD⊥AB于点D，BE与CD交于点O（如图1），则图中有相似三角形吗？有几对？ 笔者首先要求学生把可能相似的三角形一一找出来，考虑到有的学生可能观察得不细致或观察没有方法，故鼓励学生把每一对相似三角形从原图形中剥离出来，去掉干扰，这样便容易证明以下各对中的两个三角形是相似三角形，如图2～图7.
随便看	仿生机器人运动控制理论与方法研究 循环式火电厂污水处理系统的优化设计 电厂热控自动化的改造技术探索 SWT-2000型调速器在石门水电站的应用 内蒙古国电能源锡林浩特热电厂热网循环泵应用转子变频调速系统案例 10kV户外环网柜防凝露方法探究 自动化控制中弱电控制强电的方法分析 电厂热控自动化系统稳定性分析 电气设备防雷装置检测及运行维护 试论继电器在电气工程及其自动化低压电器中的实践 110kV新建变电站施工管理 高压装表接电方面存在的常见隐患及应对措施 地铁车辆中电容元件对负载性能的影响 山海关水厂供水泵应用转子变频调速系统案例 关于学习编程语言的一点建议 汽车诊断方法在教学实践中的综合应用 探讨高职心理健康课程教学对学生心理健康状况的影响 浅谈培养高校学生参与多媒体设备管理工作 轨道交通类专业1+X证书制度实践探讨 单位闭区间上帐篷映射的周期点集 金融学实践教学改革研究 互联网时代下职业院校混合式教学模式优化路径探索 关于“管理会计”课程教学改革的探索 预防小学生在体育运动中踝关节损伤的研究 以学生为本、师德重建 shiverer shiverers shivering shivers shiversome shivery shoal shoaled shoaler shoalest shoaling shoalness shoals shock shockabilities shockability shockable shockableness shock absorber shock-absorber shock absorbers shocked shockedly shockedness shockednesses r2013010010001242 r2013010010001243 r2013010010001244 r2013010010001245 r2013010010001246 r2013010010001247 r2013010010001249 r2013010010001250 r2013010010001251 r2013010010001252 r2013010010001253 r2013010010001254 r2013010010001255 r2013010010001256 r2013010010001257 r2013010010001258 r2013010010001259 r2013010010001260 r2013010010001261 r2013010010001263 r2013010010001264 r2013010010001266 r2013010010001267 r2013010010001268 r2013010010001269

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。