《高校学生创业公司工作表编排算法的研究》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

高校学生创业公司工作表编排算法的研究

范文

蒋晶晶关胜于茜孙建梅

摘要：本文以最大化满足学生志愿与工作的匹配、学生能力与岗位要求的匹配为目标，建立多目标约束的0-1规划模型，解决高校学生创业公司工作表编排问题，为该类型公司提供了科学实用的内部人员编排调整途径。

Abstract： This paper aims to maximize the matching of student volunteering and job matching， student ability and job requirements， establishes a multi-objective constraint 0-1 planning model， and solve the worksheet layout problem for college student startup companies for this type of company， provides a scientific and practical way for internal staffing and adjustment.

关键词：工作表编排;0-1规划;目标规划

Key words： worksheet layout;0-1 planning;target planning

中图分类号：TP311? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文献标识码：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章编号：1006-4311（2020）10-0218-02

1? 问题描述及算法选择

某高校学生创业公司目前有20名学生，拟将20名学生的工作岗位进行适当编排，公司根据个人表现对这些学生的综合处理能力、工作能力、技术水平和管理水平等方面进行了评价，这些学生的工作环境、工作意向、工作强度和希望学生能够达到的工作要求作为已知条件，如何在不同的岗位上分配合适的学生是研究要解决的问题。对这些学生进行工作的编排不同于对真实的公司的员工编排，每个学生每天都有课，而且每天上课的时间都不同，所以公司要从关心学生的角度出发，根据学生的工作意向来进行工作的编排，而且每个岗位的能力需求是不一样的，每个学生在每个方面的能力又是不一样的，所以这是一个很复杂的工作编排，必须要用目标规划和0-1规划来建立多目标模型，求出最优解，最大化的满足需求。

2? 问题模型

2.1 問题假设

假设现在有20名学生进行工作岗位的编排，这20名学生的课程时间、工作意向、能力水平及岗位情况、岗位要求都是已知，将这20名学生安排到这8个岗位工作，保证每个岗位每个时段至少都有一个人工作，求最优解。

①假设员工和公司的各项条件是真实客观存在的;

②总的员工满意度用代数求和方式表示，员工个人的满意度相对于所有员工总的满意度的权重是一致的;

③每个工作岗位至少分配一个人，并且要按照员工的个人意愿进行工作岗位的分配;

④员工满意度与公司满意度加权之和等于综合满意度。

2.2 问题模型

最大化满足学生志愿与工作的匹配和学生能力与岗位要求的匹配两个目标，并根据学生的课程表保证每个岗位每个时段至少有一个人在，为达到上述目标，使学生意向与岗位情况之间的差距、员工能力与岗位要求之间的差距综合最小，建立多目标约束的0-1规划模型如下。

设Xijk=1? i员工在j岗位k时段工作=0? 其他

Yijk为i员工与岗位j要求的关于能力k的等级差值（k=1，2，3，4分别表示工作能力、管理水平、技术水平和综合处理能力）;

Tik=1? i员工在k时段没有课=0? 其他

Hij为i员工对j岗位的综合满意度（Hij=ai×bij×ci），其中ai，bij，ci分别为对工作意向、岗位情况、工作时长的量化标准。Kij为i员工在j岗位上的工作能力。

Kij=公司对工作人员的能力评价等级与各岗位希望的能力等级的差值的量化标准。

总模型：Max Z=P×k+（1-P）×H，P为权重。

3? 问题求解

本模型以岗位对工作人员的合格要求作为比较的标准，将单位评价作为方案调整的设计依据，以工作意向作为最后的评判标准。

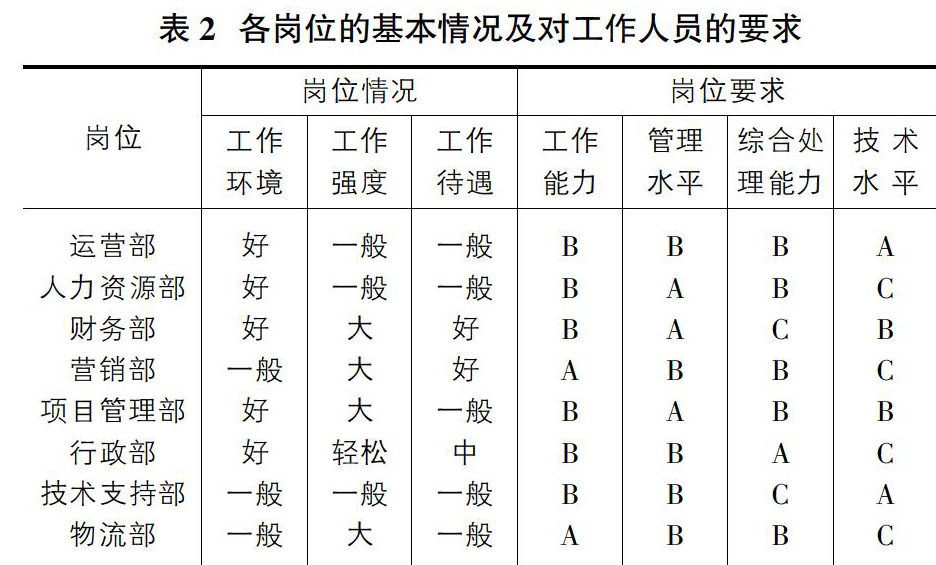
模型中设计用数字表示各种能力的评价等级，其中C代表2，B代表3，A代表4，数字越大，表示该员工能力水平越高，具体如表1和表2所示，分别表示学生工作意向及单位评价和各岗位的基本情况及对工作人员的要求。

在此，参考员工录用的实际经验：①对于某个岗位的录用人员，应尽量满足该岗位各方面能力的要求;②应尽量人尽其用;③应尽量录用个人能力满足多种能力要求的员工。因此，应使人员个人对所分配的岗位关于四项能力的差值Yijk<0的个数尽量少，要尽量使得Yijk>0，同时保证|Yijk|尽可能趋进于0。

结合表1的具体数值，再根据总结的三条经验，计算出最大值Z=15.79984，得出最优方案如表3所示。

通过工作时段与学生课程情况和表3最优人员分配方案数据代入到员工上课时间冲突模型中计算发现，项目管理部不能保证每个时段至少有一人工作，因此，通过学生个人工作意向、各岗位希望员工具备的能力等级的差值、公司对员工能力评价等级、学生上课时间三个指标发现，可以把学生19调配到项目管理部，最后得出的最优的工作编排表。

4? 模型的推广与改进

当员工的数目和工作岗位数量较大的时候，成对比较矩阵属于高维问题。需要设定一个可量化的成对比较矩阵的构造准则，例如用不同的数字表示A、B、C、D等级，并保证两两所赋值的比值不同。再结合本文模型中所规定的成对比较矩阵确定准则，根据赋值后的比值，通过相应计算软件直接输出大的矩阵，求出该矩阵的最大特征值及特征向量，并进行一致性检验。

参考文献：

[1]赵利娟.基于人性化的高职院校排课问题的最优化算法研究[J].现代职业教育，2018，5：241-243.

[2]朱艳艳，徐信叶，程朝英.预制工作表对提高医院供应室工作效率的作用[J].中医药管理杂志，2017，11：185-186.

[3]于岚，高贵晨，孙术发.基于0-1分块矩阵求解的B2C配送中心订单分批优化模型构建[J].森林工程，2019，8：233-234.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。