《基于傅里叶级数残差修正TDGM（1，1）的车流量预测模型》-工学论文，工程论文-论文范文参考-科学狗论文网

标题

基于傅里叶级数残差修正TDGM（1，1）的车流量预测模型

范文

刘素娟

摘要：车流量预测是城市智能交通研究中的热点和难点问题之一。然而，车流量受到诸多因素的不同程度的影响，使用单一模型难以对其进行准确预测。针对这一问题，本文提出了基于傅里叶级数残差修正TDGM（1，1）的车流量预测模型。该模型首先应用离散灰色模型TDGM（1，1）对原始车流量序列进行建模，并得到初始预测值以及残差序列;然后通过傅里叶级数对残差序列进行二次拟合，同时对预测结果进行修正。通过实例分析以及对比试验表明，该模型可以有效提高车流量预测精度。

Abstract： Traffic flow prediction is a key problem in urban transport system. However， many complicated factors have impact on the traffic flow prediction， which means that single model can not be used to forecast the traffic flow correctly. Aiming at this issue， a combined residual modification TDGM（1，1） model based on Fourier series is proposed for predicting the traffic flow. Firstly， this model used the TDGM（1，1） model to predict the original series of the traffic flow， and obtain the initial predicted values and the corresponding residuals. Then the Fourier series were introduced to modify the residual series and get the final predicted values. The experiments demonstrated that， in comparison with the common methods， the residual modification TDGM（1，1） model based on Fourier series can improve the prediction accuracy effectively.

關键词：车流量预测;离散灰色模型;傅里叶级数;残差

0? 引言

交通是一座城市的命脉，是城市活力与可持续发展的重要支撑。最大限度地利用道路资源，提高交通运输效能，对道路的车流量进行准确、快速的预测是当前智能交通系统发展的重要任务[1，2]。

影响车流量的因素众多、关系复杂，具有灰色特征，可以采用灰色系统理论对其进行预测。根据灰色系统理论对车流量预测时，主要以灰色模型GM（1，1）及其改进模型为主[3]。GM（1，1）模型是灰色系统模型中的核心和基础，它在有限数据的情况下有着较好的预测精度，在各个研究领域得到了广泛的应用，但仍然存在很多需要改进的问题：即可以在一定程度上降低模型拟合误差、提高预测精度，但却无法改变GM（1，1）模型本身的局限性，即利用离散方法去估计模型参数，而采用连续时间响应函数进行预测所造成的跳跃性误差。与GM（1，1）模型相比，离散灰色模型DGM（1，1）有效地避免了从离散到连续模型转换所带来的误差，其具有白指数规律重合性、伸缩变换一致性等性质[4]，但也存在模拟值只能为等比序列的问题。线性时变参数离散灰色模型TDGM（1，1）除了具有白指数规律重合性、伸缩变换一致性等性质外，还具有线性规律重合性的性质[5，6]，从而克服了离散灰色模型DGM（1，1）模拟值增长率恒定的问题。另一方面，在车流量预测过程中，线性时变参数离散灰色模型TDGM（1，1）只对车流量呈近似指数规律的单调增长序列才有较高的预测精度。但车流量的波动性将在一定程度上影响TDGM（1，1）的拟合和预测效果，因而对TDGM（1，1）进行修正是十分必要的。

针对这一问题，本文将应用傅里叶级数残差修正方法对TDGM（1，1）模型进行改进，以提高车流量预测性能。同时，结合实际车流量数据对基于傅里叶级数残差修正的TDGM（1，1）模型进行分析，验证模型的有效性和可行性。

1? 线性时变参数离散灰色模型TDGM（1，1）模型

基于傅里叶级数残差修正TDGM（1，1）模型的车流量预测方法，首先应用线性时变参数离散灰色模型TDGM（1，1）对原始车流量序列进行建模，并得到初始预测值以及残差序列;然后通过傅里叶级数对残差序列进行修正，并获得最终的车流量预测结果。

3? 算例检验

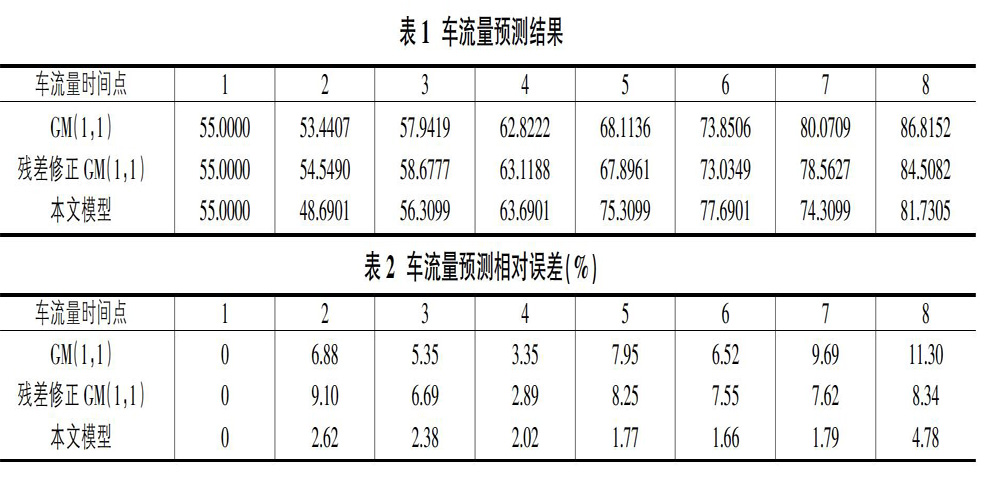
为了检验本文提出的基于傅里叶级数残差修正TDGM（1，1）的车流量预测模型，本节根据文献[7]中的车流量数据进行比较和分析。实验所用车流量序列如下：55、50、55、65、74、79、73、78，其中每项代表5分钟内通过监测点的车辆数。根据前7个数据建立傅里叶级数残差修正的TDGM（1，1）模型，并对第8个数据进行预测，预测结果如表1所示。此外，为了便于对比分析，表1也同时给出了应用GM（1，1）模型、以及基于残差修正的GM（1，1）模型的预测结果。根据表1，计算出三种方法的相对预测误差如表2所示。

从表2可知，对于第8个预测数据，相对预测误差分别为11.30%、8.34%以及4.78%，本文模型的预测效果要优于经典GM（1，1）模型以及基于残差修正的GM模型。即对于车流量预测而言，本文提出的基于傅里叶级数残差修正TDGM（1，1）模型是合理可行的。

4? 结论

本文提出了基于傅里叶级数残差修正TDGM（1，1）模型的车流量预测方法，该模型应用线性时变参数离散灰色模型TDGM（1，1）对原始车流量序列进行建模，并得到初始预测值以及残差序列;然后通过傅里叶级数对残差序列进行修正，并获得最终的车流量预测结果。实例表明，本文模型可以有效提高车流量预测精度。

参考文献：

[1]刁仁群，王伟，李剑.“互联网+交通”背景下交通大数据应用分析[J].交通企业管理，2017（04）.

[2]赵文天，万夕里，白光伟.城市交通流量预测与信号控制优化[J].小型微型计算机系统，2019（07）.

[3]李梦婉，沙秀艳.基于GM（1，1）灰色预测模型的改进与应用[J].计算机工程与应用，2015（09）.

[4]王丰效.线性时变参数DGM（1，1）变权组合预测模型[J].统计与决策，2017（13）.

[5]田英俊，宋立忠，阮苗锋.基于线性时变参数离散灰色模型的在线故障预测系统设计[J].海军工程大学学报，2018（01）.

[6]易梅，高雅萍，郭瑞雪，张文静，徐涛.动态残差修正的新陈代谢灰色模型在沉降预测中的应用[J].工程勘察，2018（04）.

[7]赵卓峰，杨宗润.基于残差修正GM（1，1）模型的车流量预测[J].计算机科学，2017（4）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。