网站首页  词典首页

请输入您要查询的论文：

　

标题 基于原点思维，培养学生“二次创造”
范文 吴华平



摘 要：在小学数学教学中，教师要担负的责任就是退回学生的思维原点，实现学生的二次创造，发展学生的数学思维。但在实际教学中，教师往往越俎代庖，限制了学生的原创思维。本文根据教学实践，提出要基于原点思维，培养学生的二次创造。
关键词：原点思维；小学数学；二次创造；课堂教学；策略研究
教育家弗莱登塔尓曾经认为，学习数学唯一的正确做法，应该是发展学生的二次创造，培养学生的原创思维。何谓二次创造？就是让学生根据自己的思维方式，重新发现问题、解决问题，实现二次创造。有基于此，教师要有意识地退回学生的思维原点，设身处地为学生着想，迎合学生已有心态，调整教学行为，不再一味地将现成的数学知识灌输给学生，而是结合学生已有能力，实施课堂探究，达到教与学的和谐共振，实现学生的二次创造。那么，到底从哪几个方面实现学生的二次创造呢？笔者现根据自己的教学实践，谈谈体会和思考。
一、基于数学现实，引领学生二次创造
在数学课堂教学中，学生的已有数学现实，是一个非常重要的教学起点。但很多教师忽视这种现实的存在，常常会根据自己的理解来进行教学设计，殊不知这样造成学生的认知流于肤浅，并不能有效培养学生的问题解决能力。一旦数学题型出现变化，学生就会束手无策，无法灵活变通。有基于此，教师要从学生的数学现实入手，退回到学生的知识和逻辑起点，以此作为教学设计的基础，引领学生自主探究，发展二次创造。
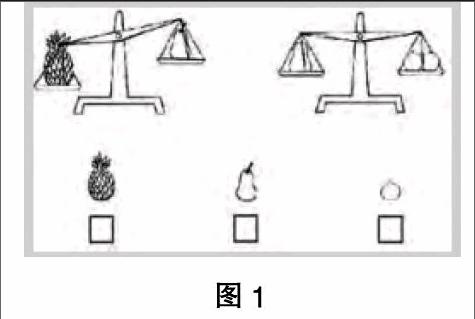
例如，在教学一年级教材《比一比》的课堂练习时，有这样一道比较轻重的思考题（如图1所示）：在最重的下面打对号，最轻的下面打叉。
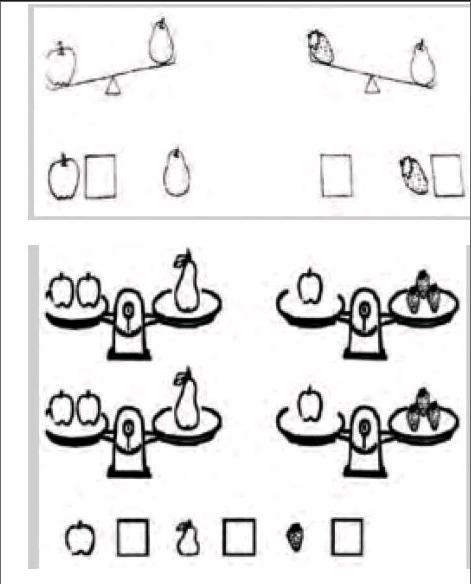
这道题对于一年级的学生来说存在一定的难度，因为教材中原有的内容是关于一架天平不平衡的情况，学生根据自己坐跷跷板的生活经验，认为沉下去的一边是重的，翘上去的一边是轻的。这样就可以很快比较出轻重来。但这道习题中是两架天平，而且一个平衡，一个不平衡，学生会出现困惑。根据这一数学现实，笔者结合学生的思维原点，特意设计了图2（如图2）来进行有效过渡和转化，引领学生展开探究思考。
在图2中笔者设计了两个层次的过渡，第一个层次先让学生观察苹果和梨、梨子和草莓，根据天平的不平衡来判断这三种水果的轻重。学生观察后认为苹果比梨重，梨比草莓重，由此很容易得出苹果最重，草莓最轻的结论。第二个层次，学生根据两架平衡的天平，得到清晰的认知，从而顺利完成思维过渡，实现了二次创造，学会了推理和判断。
以上教学，教师有效把握学生的数学现实，以此退回学生的原有思维原点，以此为起点进行教学设计，给学生搭建了一个有效的探究平台，通过观察和比较，引领学生一步步实现了思维发散，由此开拓了学生的二次创造，实现了原创思维。
二、基于思维方式，促进学生二次创造
在日常教学中，学生都有自己的思维方式，在处理一些数学问题时，不但会有自己的惰性和惯性思维定式，也会有自己的独特优势和创新思维。然而教师往往忽略这些，只教给学生单一的解题思路，导致学生无法融入课堂思维，无法实现自主思考。此时，教师就要退到原点，基于学生的思维动向，为学生提供交流和展示的空间，让学生通过自主探究实现数学再创造，从而提升学生的应用能力。
例如，在教学苏教版教材《用连除法解决实际问题》时，笔者先出示一个主题图，让学生观察图示中的数量关系：有两个书架，每个书架有4层，一共有232本书，而后放手要学生根据已知信息提出问题并进行解答。此时，笔者将学生分成五人为一组进行交流，学生提出问题：求平均每层书架放多少本书，并进行讨论解答。得到了以下几种方法：第一种，先算出每个书架放的书的数量232÷2=116，再算出每层书架的数量116÷4=29（本）；第二种方法，先算出两个书架一共有几层4×2=8（层），再算出每层放多少本书232÷8=29（本）。此时笔者并不急于教给学生更多的方法，而是让学生自主探究：想一想，还有没有其他的方法？学生认为，可以先求出232÷4=58，然后再求出每层书架放的书58÷2=29（本）。这种与众不同的解题方法得到了一部分学生的反对，此时笔者让学生说说想法，学生认为，列式232÷4是先将两个书架并排放置，这样就表示新拼起来的大书架一层有58本书；然后列式58÷2就表示原来每层书架平均放多少本。通过这样的交流，学生自由展现自己的思维方式，从而促进了学生的二次创造，发展了学生的数学思维。
以上教学环节，教师给学生提供了独立的空间和时间，让学生独立思考，合作交流探究，每一个学生都有自己的思维方式，得到了全面的展示，对一些另类的解法也进行了有效的自主沟通和交流，从而实现了学生思维的和谐共振，在一个有效的课堂教学中达到二次创造。
三、基于思维过程，实现学生二次创造
在新知建构中，面对教学难点，教师要退回学生的原点，给学生提供一个有效的思维过程从学生的视角设计教学情境，把握思维流程，让学生参与整个过程，从而实现学生的二次创造。
例如，在教学苏教版教材《圆柱和圆锥》这一内容时，笔者设计了这样一道习题：一支牙膏出口处直径为5毫米，小明刷牙每次都挤出12毫米长，这只牙膏他可以用36次。后来这种牙膏进行了改装，直径改为了6毫米，小明还是习惯性挤出12毫米长来刷牙，新包装的牙膏他可以用多少次？这道题一开始学生都认为简单，结果算了半天，才发现原来计算非常烦琐，要先算出牙膏的体积：3.14×（5÷2）2×12×36=8478（立方毫米），然后再算出新包装后用的牙膏量3.14×（6÷2）2×12=339.12（立方毫米），最后再拿牙膏的体积除牙膏量8478÷339.12=25（次）。有没有更为简单的方法呢？学生探讨后认为可以用方程来计算。设新包装后的牙膏可以用x次，列式为3.14×（6÷2）2×12×x=3.14×（5÷2）2×12×36，根据等式的基本性质，方程可以简化为9x=（5÷2）2×36，x=25。通过这样探究，大家都发现了更简便的方法。有的认为，原来的牙膏和新包装牙膏的底面直径的比是5∶6，底面积的比就是52∶62，也就是25∶36，新包装前能用36次，包装前后的牙膏总体积不变，因此挤出的量和使用的次数是成反比例的，新包装的使用次数就是25。
以上教学，教师退回思维原点，让学生经历整个思维过程，因势利导，带领学生从烦琐的计算到解方程，再到用比例来进行推导，整个过程思维层层递进，顺利实现了二次创造，从而有效提升学生的思维能力。
四、基于思维障碍，发展学生二次创造
在教学中，当学生出现思维障碍时，教师不要强势地进行批评和指正，更不能越俎代庖，而是要基于这一障碍，退回到学生的原点，设身处地与学生的认知学情顺应和契合，避免思维“教师化”，做到“学生化”，从而找到有效的解决办法，发展学生的二次创造。
例如，在教学六年级内容《百分数的应用》时，有这样一道习题：妈妈四月份工资纳税385元，根据个人所得税的标准：超过2000元以下不纳税，月收入超过2000纳税，不超过500元的部分，5%；500～2000元的部分，10%；超过2000～5000元的部分，15%。问妈妈四月份工资是多少元？这道习题有49%的学生都做错了。主要障碍在于，大家不知道分段计税的含义，不能够逆向思维。根据这两个思维障碍，笔者进行了三个阶段的设计。第一个层次，要学生找一找，在题目中分段计税的标准有哪些。等理顺这个问题之后，第二个层次，笔者要求学生算一算工资3500元、3900元和4500元分别要纳税多少。学生根据分段纳税，找到对应数量关系之后，算出纳税钱。第三个层次，要学生算出纳税385元工资应该是多少。通过三个层次的引领，学生一步步找到了问题解决的关键，从而有效发现了自己的错误所在，突破了思维障碍，完善了自己的二次创造，提升了数学思维。
以上教学，教师基于学生的思维障碍，退回思维原点，顺应学生的思维层次，分层设计引领，让学生自主探究解决，从而促使学生积极思考探究，强化了对障碍根源的认识与分析，提高了“免疫力”。
总之，教师退回思维原点，是对学生的尊重和理解，更是顺应学生主体，能够发展二次创造，有效提升学生的数学学习能力。
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 4:03:12