网站首页  词典首页

请输入您要查询的论文：

　

标题 数学，向思维更深处漫溯
范文 张丽



摘 要：“数学教育要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力方面不可替代的作用”，这是对数学教育价值的一个深刻阐述。义务教育阶段是一个人的思维能力发展的关键时期，小学数学课程要为学生的思维能力的发展奠定坚实基础。要培养学生的思维能力，必须给学生进行数学化思维的机会。为此，教师要精心设置需要学生做出逻辑判断的问题情境，设计引发学生独立思考的教学过程，营造引起思维矛盾冲突的交流机会，让学生充分运用数学化思维发现问题、提出问题、分析问题和解决问题，真正将学生的思维活动有机融入学习过程。
关键词：数学思维；激活；促进；拓展
在小学三年级《数学广角——重复问题》的教学实践中，笔者以“激活思维——促进思维——拓展思维”为主线，使学生在数学活动中展现思维过程，在操作体验中得出理性认识，提炼为数学化的思考，并能转化为数学应用，有效地培养与发展了学生的数学思维能力。
片断一：
1. 谈话引入：老师了解到几个小朋友参加特长班学习的情况（课件出示舞蹈班：3人，英语班：4人，但不出现实际姓名）
2. 师追问：一共多少人？说理由，写出算式3+4=7。
3. 依次念出参加两个班的学生名单并上台，数出学生人数，制造冲突。
师：咦，怎么统计出来只有6个人？是我们算错了吗？板书：3+4=6？
【分析】巧设情境，在矛盾中激活思维
要培养学生的思维能力，就必须为学生提供进行数学化思维的机会。课始，运用与学生实际相关的“人数”情境，需要学生做出逻辑的思维判断，但是常规的判断与现实产生冲突，由此引起学生思维矛盾的交流机会，让学生充分运用数学化的思维去发现问题，激发其探究欲望，激活学生思维状态。
片断二：
1. 分类统计，感受重复
请6位学生上台，用举手的方式表示。舞蹈班3人，英语班4人，总人数6人。
学生发现有一人举了两次手，提出质疑：不对！杨诗桐举了两次手。
师：举两次手说明了什么？
生1：杨诗桐学了两样。
生2：杨诗桐既参加了舞蹈班又参加了英语班。
师板书：既……又……
出示学生分类名单：
师：我们一起来看看老师的统计表，是不是和你们说的一样呢？
学生从统计表中发现，杨诗桐的名字出现了两次，由此感受“重复”，教师板书“重复”。
2. 站队活动，体验重复
师：为了让大家看得更明白，请6位孩子分开站，舞蹈班的站左边，英语班的站右边。
学生按要求站队，出现杨诗桐两边跑的情形，最后选择了站在中间。
师：为什么杨诗桐要站在中间呢？
生1：因为她参加了两个班。
生2：因为她既是舞蹈班的又是英语班的。
3. 几何直观，呈现重复
小组讨论一下：有什么办法能记录下这样的站位关系，让我们一目了然地知道这个孩子既参加了舞蹈班又参加了英语班？
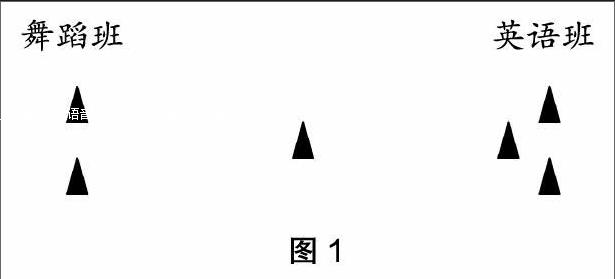
教师根据学生的回答，用三角形在黑板上表示这样的位置关系（如图1）。
师：这样的图形真能让大家都看明白吗？
学生观察，交流后发现问题：这样表示，如果不作解释的话，中间的那个三角形我们不能确定它究竟属于哪个班。
师：怎样表示不用解释，也能让别人看明白？
生1：可以给每个班划定一个范围，三角形就放在那个范围里。
生2：用圈把它们圈起来，一个圈表示舞蹈班，一个圈表示英语班。
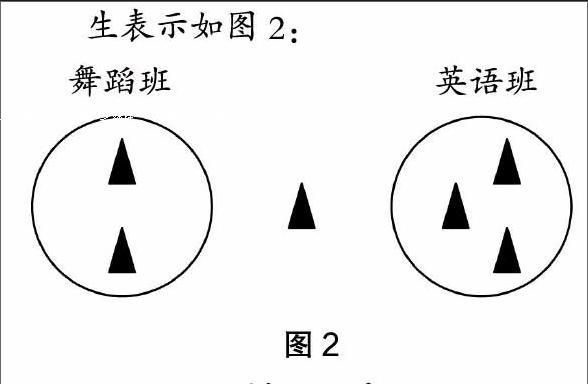
师顺势拿出红、黄两个圆圈教具，请一学生上台演示如何使用这两个圈表示位置关系。
生表示如图2：
师再问：这样可以看明白了吗？
学生有的说可以，有的说不行。
生：这样把中间的杨诗桐排除在外了，她既没在舞蹈班，又没在英语班。
师：难道没有办法了吗？
小组再次讨论，想一想，再在练习本上画一画，找到解决问题的办法。
请一个小组的学生上台演示讨论结果，如图3：
4. 揭示图意，理解重复
师：这两个圈出现了什么现象？为什么将它们交叉重复呢？
生：两个圈重复了，中间的杨诗桐才能同时在两个圈里。
师：这一重复，使原来的两个圈形成了三个部分。
学生交流图形每一部分所表示的意思，理解“只……没有……”和“既……又……”的部分。
【分析】体验探究，在直观中促进思维
在“自主建构，体验集合”的环节中，集合图的形成是教学难点，在学生用语言描述说不清道不明时，便产生了一种强烈的需求：用什么方法可以一目了然地表示出“重复”的现象？
在这样的需求下，教师设计了以下三个层次的活动。首先，采用举手、观察表格、站队等多种统计活动，让学生经历了感受重复、体验重复的过程，明白矛盾引起的原因，由此引发学生思考，为由情境语言转化为图形语言作了良好的铺垫。其次，通过学生交流，挑起学生质疑，在辩与引中学会用符号与图形表示，逐步形成集合图，有效地沟通了情境语言和图形语言的联系。最后，凭借直观的集合图，理解数量与数量之间包含与排除的关系，在分析图意、表达图意的过程中培养学生识图能力和整理信息、表达信息的能力。
这个过程有效引导学生借助几何直观、数形结合，启迪思路，把复杂的数学知识变得简明形象。在整个探究活动中，学生一步步揭开并自然而然地建立起重复的概念，然后通过分析图意、完整描述图意、分析数量关系，深度理解集合概念的意义，引领学生经历“猜测——判断——交流——辨析——评价”的完整思维过程，促进了学生数学思维的发展。
片断三：
1. 课件出示：舞蹈班4人，英语班5人。讨论：你们认为一共有多少人？
生（大多数学生）：一共有9人。
师：9人，可以吗？
生1：不一定是9个人，万一舞蹈班和英语班的活动时间不一样，有一个人既在学舞蹈又在学英语，那就只有8个人了。
师：可能出现重复的现象，是吧？
（许多只小手高高举起，孩子们急于想表达自己的意见。）
师：看来孩子们的想法不尽相同，请你们在空白的集合圈中画一画，然后在小组内交流一下，并算出每一种情况下，参加两个小组的人数一共有多少人？
学生自己选择方法在集合圈中表示出参加课外小组的人数，并列式计算，再交流。经过全班整理，依次完善下表：
师：为什么同样是4人参加舞蹈班、5人参加英语班，结果会出现不同的情况呢？生讨论并交流。
生1：重复参加两个组的人是几，就减几。
生2：重复的部分越多，参加两项活动的人数就越少。
生3：我发现最多只能重复4人，如果重复5人的话，舞蹈班有5个人了。
【分析】巩固深化，在开放中拓展思维
数学思维过程中具有最高品质、最高层次，而又最可贵的是创造性思维。因此，教师要以学生掌握基础知识、基本技能、基本方法为根基，设计可以唤醒学生好奇心的“开放性问题”，引导学生打破常规、独立思考、大胆猜想、质疑问难、积极争辩、寻新求异，将数学结论还原为让学生自己经历抽象和归纳的思维过程，以此拓展学生的思维方式，发展他们的创新思维。
本节课的练习设计选用开课时的情境，避免学生思维不断转场。将信息改为“舞蹈班4人，英语班5人，一共有多少人？”鼓励学生运用所学知识大胆推测与想象：4个人和5个人，一定就是9个人吗？而解决这一问题，又回归到探究新知时采用的符号化思想与几何直观，让学生经历抽象与归纳的思维过程，使学生能用符号与图形展示出自己不一样的思维过程，最后在列表总结交流中巩固完善了学生对“重复问题”和“集合圈”的认知。这类开放题的训练，让学生感受到数学的价值与魅力，给学生提供自由的思维发展的时空，激活了学生多角度多层次的思维，增加了思维的灵活性、变通性与创造性，从而有效地拓展了学生的思维能力，增强了学生的创新意识。
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 23:45:13