网站首页  词典首页

请输入您要查询的论文：

　

标题 借助“示错”策略 优化概念教学
范文 余静


摘? 要：概念教学是小学数学教学中的重点内容，小学生在学习数学概念的过程中经常会出现认知上的错误，这种错误是一种有效的教学资源。借助“示错”策略能够有效地优化小学生的概念学习。基于此背景，本文对引入概念时“示错”，强化概念感知;形成概念时“示错”，促进概念形成;巩固概念时“示错”，深化概念理解的策略进行了探究，希望能达到一定的借鉴意义。
关键词：概念教学;数学概念;示错
在小学数学知识体系中，数学概念是重要的组成部分，也是重点教学内容，因为小学生要想系统地学好数学知识，就必须先理解数学概念才能实现。数学概念具有抽象化的特征，小学生有关数学的“前概念”或负迁移等都会对数学概念的理解产生影响，从而出现偏差。《数学课程标准》强调教师在开展教学时，要以学生已有的知识经验为基础。小学生对数学概念的理解往往会存在错误，在小学数学概念教学中，教师要大胆地把学生的错误展示出来，并以此为教学资源引导学生进行深入学习，以便学生在观察和思考错误中实现有效反思和探究，从而达到概念学习的高效化。
一、引入概念时“示错”——强化概念感知
小学生的生活经验会让他们对数学概念的理解产生一定的影响，在对一些数学概念的感性认识上，往往有一些错误的认知。教学中，教师有必要直面学生的错误，通过主动示错的策略强化他们对正确数学概念的感知。
例如，一位教师在教学《平行四边形的面积》一课时，有这样一个教学片段：
师：今天我们要学的内容是“平行四边形的面积”（边说边板书）。请大家看大屏幕，有一个底为8厘米，侧边长为5厘米的平行四边形，这个平行四边形的面积有多大？（多媒体展示所描述的平行四边形）
生：面积应该为40平方厘米。
师：能说说你怎么算出来的吗？
生：由8×5=40得到的。
师：这样算的原因是什么？
生：我从长方形面积计算公式得到的启发，用“底×边”来计算平行四边形的面积。
师：好像说得也不错。那请大家利用格子图来对其面积大小进行验证好吗？（边说边拿出格子图，并把图形置于其中）
师：请大家数数看，它的面积是40平方厘米吗？
（学生数格子后得出其面积大小为32平方厘米，于是引起了讨论。）
生：这个面积不是40平方厘米，说明刚刚采用的计算面积的方法不对。
以上教学片段中，学生利用了“前概念”——长方形的面积计算方法来类比平行四边形，出现了错误。而教师主动利用了学生的感知错误，及时让学生在自主探究中纠正其“负迁移”，让学生的探究热情越发高涨。在此基础上，学生进行的探究活动必然是高效的，有利于有效建构其有关平行四边形面积计算的本质特征。
二、形成概念时“示错”——促进概念形成
在小学数学概念教学中，促进学生形成数学概念是教学的重点。而很多无关紧要的因素会影响到学生理解数学概念的准确性，进而出现偏差。为此，这些偏差就应被主动地呈现于学生眼前，让学生投入对自身思考结果的反思中，促使他们更深入地理解概念的本质规律。
（一）借助“示错”，把握概念要素
小学生处于思维发展阶段，因而思维缺乏严密性，这让他们很难对相关概念的关键点进行准确的把握，以致出现一些错误的理解。为了让学生对概念的不同要素有更清晰的把握，教师可通过“示错”的方式来进行概念教学。
例如，一位教师在教学《角的认识》一课时，有这样一个教学片段：
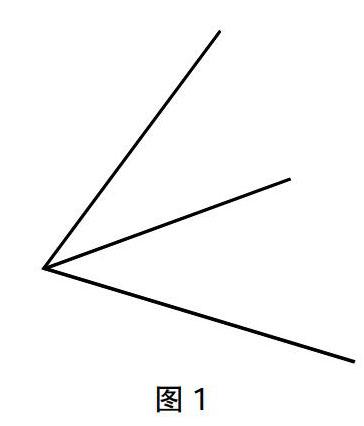
师：从前面的学习中，我们了解到角是由一个顶点和两条边组成的。那么，请观察如下图形，数一数角有多少个？（图1）
生：一共是2个角。
师：请同意他说法的同学举手示意。
（很多学生纷纷举起手来。）
师：那现在请一个同学上讲台告诉我们有哪两个角好吗？
（学生在指的过程中发现自己在观察时忽略了一个角。）
生：老师，这里一共是3个角，刚才数错了。
师：多的那个角在哪里呢？
生：这外面的顶点和由其出发的两条边也能形成一个角。
师：也就是说，在观察角的组成时，只要能找到一个顶点和由其出发的两条边，就可以说它是一个角。那大家再数数这个图形里的角的个数吧。
以上教学片段中，学生只从表面观察了数学角，所以一开始只找出了两个，教师则让学生在指明角的过程中去发现错误并数出正确的个数。学生通过细数意识到自己的认识错误，从而更深刻地理解了角的“一个顶点和两条边”的组成概念。
（二）借助“示错”，引导概念辨析
小学生在学习数学概念的过程中往往会存在表面化的现象，教师要借助“示借”策略，引导学生进行概念辨析。
例如，一位教师在教学《轴对称图形》一课时，有这样一个教学片段：
师：我们刚刚对轴对称图形的概念进行了学习。那请大家对屏幕上所展示的一系列图形进行观察，判断它们是否属于轴对称图形？（边说边在屏幕上放出正方形、平行四边形、三角形和圆）
（对于平行四边形是否为轴对称图形，学生们持有不同的意见。教师抓住这一契机引导学生进行辩论赛。）
生1（正方）：我方认为，平行四边形属于轴对称图形，我们可以沿其中间剪成两部分，所得两部分一模一样。
生2（反方）：我方认为这种说法是错误的。虽然两边完全一样，但沿中间对折后，平行四边形的两边是无法重合在一起的。
生3（正方）：请看我的操作，先用剪刀沿其中间剪成两部分，然后观察发现两邊是一样的图形，所以它属于轴对称图形。
生4（反方）：你用裁剪的方式得到的结论是不对的，应该通过对折看其是否重合。
（生1听后开始对折平行四边形，发现不管怎样都无法保证两边是重合的。）
生1（正方）：是我理解错了。要让平行四边形沿中间分开的两部分能重合，不能通过对折来实现，而必须要用裁剪的方式才能做到，这和轴对称图形的定义是不相符的。
以上教学片段中，教师巧妙地抓住了学生的思维错误，引导学生通过辩论的形式来加深对“轴对称图形经过对折，能让两边重合在一起”的理解，推动学生对轴对称图形概念的准确把握。
三、巩固概念时“示错”——深化概念理解
除了让学生学习新的数学概念，还应及时地进行巩固，这也是非常关键的。教师在组织学生巩固概念时，应主动呈现出学生所犯的错误，从而纠正学生的思维，加深已掌握数学概念的印象。
（一）借助“示错”，理解概念本质
教师对小学生开展概念教学时，应注重引导学生把握概念的本质特点。为此，可通过“示错”的方式来达到这一目标。
例如，一位教师在教学《认识分数》一课时，有这样一个教学片段：
师：请大家观察，用“1/2”来表示下图的涂色部分正确吗？（图2）
生：是错的。涂色和不涂色两部分是不相等的。
师：那能否用所学的分数来表示其涂色部分呢？
生1：不行。
生2：我同意。这个图形的分割方式不是平均的，所以无法用分数对其进行表示。
师：那我现在再为它添上两条线，大家再观察一下，想一想可否用分数对涂色部分进行表示？
生3：这样划分之后就可以用“1/2”来表示它。
师：为什么这样就可以呀？
生3：因为加了两条线后，整个三角形被均分为4份，而有一份被涂上了颜色。
生4：我明白了，今后遇到类似的问题，我们应该从不同的角度去观察其分割方式是否为平均的。
生5：从这个题中我们也可以明白，在观察图形时，常常会出现表面看上去未平均分的现象，但通过深入观察和分析后，仍可得出其是平均分的。
以上教学片段中，教师没有避开学生因思考缺乏周密性而出现的错误，而是引导学生去发现思维错误，进而让他们体会到图形的均分与否仅从表面去观察是不对的，应该深入图形特征进行分析和思考，从而揭示出图形平均分的份数，确定用哪个分数进行表示。这对强化学生理解分数概念的程度具有重要意义。
（二）借助“示错”，理解概念内涵
對于数学概念内涵的深刻理解，教师也应用“示错”的方式来开展概念的教学，以实现更加高效的概念学习。
例如，一位教师在教学《等腰三角形》一课时，有这样一个教学片段：
教师为学生设计如下题目：有一个等腰三角形，其三条边中有两条边已知，分别是2cm和5cm，那么，请问其周长为多少？
生1：假如5cm的边为它的腰，那么周长等于5+5+2=12cm。
生2：假如2cm的边为它的腰，那么周长等于5+2+2=9cm。
师：请大家把题目所描述的三角形
画在草稿本上好吗？
（学生着手绘制三角形，教师让学生表达自己的想法。）
生2：老师，我刚刚的回答是错的。因为如果腰长为2cm，那么两腰的和小于第三条边。
生3：我同意，因为2+2<5，而三角形任意两边的和应该大于第三边。
生4：虽然等腰三角形不是普通的三角形，但它同样要符合一般三角形的基本规律，我们要注意题目给我们挖的陷阱。
学生在学习等腰三角形时，往往只注意保证其两条腰的长度一致。而在上述教学片段中，教师从学生的错误点着手，让学生自行绘制自己得到的等腰三角形，这样学生通过动手操作发现腰为2cm时不能形成三角形，这对学生巩固已学的三边规律的知识有着重要的作用。
综上所述，把“示错”策略引入概念教学之中，能有效地把握学生理解概念时的偏差原因。同时，把“错误”展示出来，还有利于学生思维的活跃，让他们在学习数学概念时实现更高的效率。
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/4/17 1:48:08