《基于混沌的图像加密方法研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

基于混沌的图像加密方法研究

范文

党小娟++甘霖++朱家云

摘要：运用混沌函数可以快速生成比较稳定的伪随机序列，可以满足伪随机序列所需。从密码学的领域来看，对混沌理论非常关注，并且研究过程中获得了丰富成果。但是混沌理论研究者并没有由此而放松，再进一步进行更深入、更透彻的研究。本文就是在混沌理论备受关注形势下，深入研究基于混沌图像加密算法。

关键词：混沌；图像加密；研究

中图分类号：TP301 文献标识码：A 文章编号：1009-3044（2016）17-0224-02

1 前言

自从计算机技术出现以来，互联网所具有的特性就被人们所关注。在该环境下，人家可以做各种想做的事情，比如通过互联网对各种文本、视频以及音频等信息进行处理，并且这些信息数据中都包含了需要传输的私密图像信息。但是随着互联网的空间不断开放，传输机密信息的危险性非常大。因此在传输机密图像信息过程中，就必须要对图像加密与解密，才能够确保传输过程的安全性。在这种形势下，研究图像的加密方法具有实用价值。

2 引用混沌密码学的必要性

混沌密码学就是将混沌理论融入到密码学中就成为一种交叉学科，该学科被人们高度关注。因混沌系统拥有的独特特征比较适合密码学。自然也就是被密码学的研究高度重视。但是互联网技术不断安放在，人们从网络中需要传输的信息不断增多，特别是一些图像数据占据着重要比例。主要是混沌比较适合使用在图像加密中；同时人们对传输图像的安全性要求不断提高，因此研究这种图像加密算法属于热点问题。听过研究人员不断努力，混沌理论研究上逐渐趋于成熟，也在该图像加密的算法上获得了一定成就，不断提出了一些经典的加密算法。而且混沌理论就要有为随机性，初值比较敏感等各种特征，而且这些特征和密码学的特征比较吻合。当然引入了混沌理论，也促进了密码学的快速发展。通过这种混沌理论就能够设计出更多的算法，并且各种算法都具备极好的安全和加密速度，同时数字图像不断普及，特别是在互联网中传输的图像不断增多，人们也就更加重视所传输图像自身的安全性，这些因素都能够推动这种加密算法的快速发展。

3 基于混沌的图像加密方法

和本文数据相比较，图像数据具有独特性质，因此对于图像的特性，假如依然采用文本加密算法，根本无法满足效率所需。因此加密算法必须要针对其自身特性，合理选择设计。

3.1 图像加密算法

（1）图像像素空间的置乱；采用二维仿射变化置乱图像的方法主要有：二维Baker图像的置乱变换、二维Fibonacci—Q图像置乱变换以及二维Amold图像置乱变换。而时常所用像素位置的改变置乱方法有：基于Hilbert曲线图像置乱方法，基于生命游戏图像置乱方法，基于换幻方图像置乱方法等等。

首先二维Arnold变换图像置乱方法；假设单位上存在一个点坐标（x，y），可得出点（x，y）变化到点（x，y）变换是：

其次改变图像像素的置乱法，这种方法就能够把像素矩阵和某一类矩阵进行变换过程形成对应关系，就能够形成了像素迁移路线，当然要确保首元素与尾元素是不可能形成回路。像素就会顺着转移路线移动，必定改变了像素的位置，如果把原始图像像素从头到尾移动一遍，就完成了图像加密。

（2）扩散图像的像素值；当对图像像素空间实施置乱之后，并没有改变图像的像素值，而且置乱前后图像中直方图并没改变，但是要提升图像加密安全性，还必须要替换图像的像素值，也就是扩散图像的像素值。当然扩散图像的像素值方法并不是唯一的，而是有许多种，可将像素值映射至其他区域来选择计算像素本身，可在相邻像素间采取异或运算等。

3.2 基于混沌的图像加密分析

因混沌系统自身特性与密码学特征比较相似，因此把混沌使用到密码学中具有极大的前景，将这种理论使用到伪随机序列的生成器。无论是置乱图像的像素还是扩散像素，伪随机序列都发挥着重要的作用。尤其是置乱像素过程中，就能够通过这种序列转换矩阵；在扩散像素中，就能够通过这种序列改变像素值，当然也可以采用这种方法为扩散算法实施选择。

实施图像加密的主要目的就是将图像中所携带的信息隐藏起来，就算攻击者通过非法手段获得加密图像，也不可能从图像中获得所需要的任何信息，加密时，大部分都是通过两个步骤实现，即为置乱图像的像素空间和扩散图像的像素值。如果加密系统的安全要求并不高，并且要提升加密速度，处理过程中只需要图像置乱或图像扩散即可。但是系统加密需要的安全性比较高，那么就应该多次迭代图像置乱与图像扩散，从而加强加密的效果。基于混沌的图像加密方法，其一般数学表达式为：[R=Da（Cb（P，Kc），KD）]；该式中P表示明文，R为密文，C为置乱函数，D为扩散函数，[Kc]值为置乱函数的密钥，[KD]为扩散函数的密钥，a为扩散次数，b为置乱次数。基于这种加密的密钥空间，就可采用如下式子进行表示：[S=（Sbc，SaD）]；在此式中，[Sbc]即为置乱秘钥的空间，[SaD]为扩散秘钥的空间。

3.3 设计步骤

因为混沌理论照中包含着许多内容，比较常见的混沌函数有一维，二维以及三维区分，在设计加密算法就只需要采用一个混度系统，当然也可以使用到多个系统之中。因此设计该算法之时，就必须要考虑到加密系数所用环境，还必须要满足加密速度以及安全性的要求。如果加密速度的要求不高，但安全性要求不高，就可以采用一维或者二维混沌系统设计加密算法；但是安全性的要求比较高，加密速度较低，就要设计加密复杂一些，如采用三维混沌系统。本文就以一维Logistic映射函数探讨混沌加密法。

（1）加密算法

因为一维函数比较简单，就是因为简单研究过程相对比较容易，并且极易进行控制。相对而言，一维函数比较成熟，因此在图像加密算法中使用比较广泛，并且也成为一种比较优秀的加密算法。这种加密算法的速度较快，并且因研究比较透彻，所以算法也比较稳定可靠。其迭代公式为：[XL+1=uX1（1-XL）]。

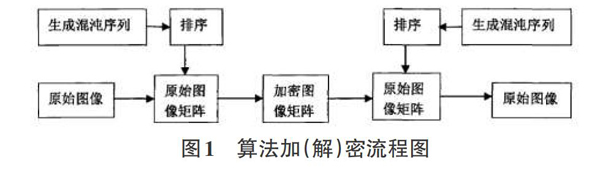
当3.56994564时，一维混沌迭代序列必然会收敛到一个特定值。该算法加（解）密的流程如下图所示：

图1 算法加（解）密流程图

其一，提取出原始的图像矩阵P，大小是m*n（原始矩阵的行像素数为m，列像素数为n）；

其二，取[x0∈（0，1）]，那么[u∈（3.5699456，4）]；重复迭代计算m*n次，就能够得到一个长度是m*n，具备伪随机性、不重复序列为；

其三如果对多得到的序列X排序时，排序标准可以从小到大顺序，也可从大到小顺序，本文就是以从小到大方式排序，这样就能够获得有序序列；[X=（x1，x2，……，xm*n）]

其四依据X中各元素处于Y中位置，就能够获得索引向量为[Index=（d1，d2，……，dm*n）]；[di∈（1，2，……，m*n）]，而且Index中各个元素都不相等，

而索引向量也是矩阵进行置乱像素的基本依据，把向量Index依照列重构，就能够得到一个矩阵，其大小是m*n，这个矩阵就是位置矩阵。

其五按照位置矩阵中所对应的元素值就能够把原始图像置换成大小相同的矩阵S，S=P（L），最终所得S即为加密图像矩阵。在这个过程中[x0]与U即为算法中两个密钥。最终结果如图2、图3所示：

参考文献：

[1]王兴元.复杂非线性系统中的混沌[M].北京：电子工业出版社，2013.

[2]关新平，范正平，陈彩莲，等，混沌控制及其在保密通信中的应用[M].北京：国防工业出版社，2012.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。