周凯 邬学军 沈守枫
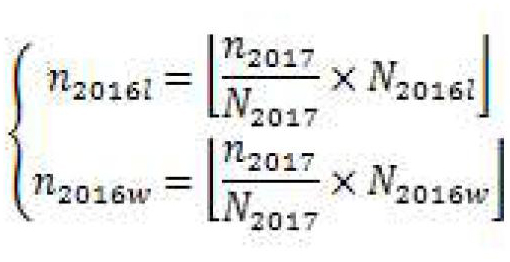
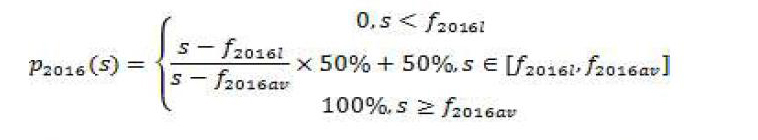

摘要:针对2017年浙江省新高考模式下,历年招录数据参考价值受限问题,该文提出了一种基于“文理等位分”思想的志愿填报数学模型。首先,论文汇总近年浙江省普通本科招录的电子数据,完善系统数据库;然后,基于等位分思想建立数学模型计算考生被各全国高校各专业的录取概率;最后,基于高校综合排名与专业排名对可供推荐的志愿进行排序,并完善学生的80个志愿推荐。
关键词:新高考;文理等位分;数学模型
中图分类号:TP3 文献标识码:A 文章编号:1009-3044(2018)19-0018-02
Abstract: In order to solve the problem of limited reference value of recruitment data in the 2017 new college entrance examination model in Zhejiang Province, this paper presents a mathematical model of voluntary application based on the idea of "equal score of arts and sciences". First of all, the paper summarizes the electronic data of ordinary undergraduate recruitment in Zhejiang Province in recent years, and consummates the system database. Then, based on the idea of allelic score of arts and sciences, a mathematical model is established to calculate the probability of candidates being admitted to various majors in colleges and universities throughout the country. On the basis of comprehensive ranking and professional ranking of colleges and universities, we rank the recommended volunteers, and perfect the 80 voluntary recommendations of students.
Key words: College entrance examination voluntary; equal score; mathematical model
1 引言
作為我国新一轮高考改革的试点省,浙江紧密结合省情特别是教育发展现状特点,经过两年多的探索,走出了一条既体现浙江特色,又能为国家层面深化考试招生制度改革提供借鉴推广范本的高考改革之路。
2017年,浙江省的新高考出现了以下几点变化:以“3+3”和“7选3”方式扩大学生的选择范围,把更多的选择权交给学生和学校。根据新的考试科目设计,学生能有35种选择,完全打破了传统文理分科的局限[1]。浙江新的录取方案取消录取批次划分,所有高校实行“同台”无差别竞争。在此基础上,由以前的以院校为投档单位改成以专业(类)为投档单位。按考生成绩分段填报志愿、分段录取;从学校平行志愿,变为专业(类)平行志愿。普通类高考考生可填报80个专业平行志愿,专业平行志愿投档,将依据考生位次、志愿顺序进行。计算机对考生所填报的80个志愿依次检索,一旦符合投档条件即直接投档到该院校专业。许多高校为了适应新高考重新调整了招生专业门类。为了让考生有更大的选择余地,许多高校将原有的小类招生调整为大类招生,甚至将几个大类进行合并。学生在第一学年按照大类培养,在第二学年开始专业分流。如此大的变化,使得原有浙江省的高考录取数据变得无法直接参考,使得考生和家长更为困惑。由于今年是实行新高考的第一年,国内尚无关于志愿填报方案的模型可供参考。因此,开发一个有效的高考志愿填报数学模型对于指导考生和家长合理填报志愿是非常有必要的。
2 基于文理等位分的录取概率模型
考虑到2017年浙江省新高考政策下,文理不再分科招收学生。本录取概率计算模型建立的前提基础为:假设所有同学的录取顺序仅与考试排名有关。所以,需要将考生在2017年的考试排名转换成历年的文理综合排名[2]。首先,论文收集2010-2016年浙江省高考的招录结果(包括各校各专业的录取最低分、最高分、平均分),浙江省历年高考的一分一段数据、2016年武书连高校排名等信息,建立完善的电子信息库。
假设当考生的分数与某学校某专业录取最低分相等时,认为被该学校该专业录取的概率为50%;同时,当考生分数等于或高于学校专业录取平均分时,认为被该学校该专业录取的概率为100%。而当学生发分数位于该分数段之内时,录取概率与学生分数呈线性相关。综合上述假设,得到学生的录取概率计算模型[3-4]:
3 基于层次分析法的学校评价模型
层次分析法是由美国著名的运筹学专家Saaty首先提出的,它将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。该方法通过比较确定各准则对于目标的权重,以及各方案对于每一准则的权重[5-6]。
4 结束语
该模型充分综合考虑影响志愿填报的因素之间的关系,采用层次分析方法对高校评分进行精确分析,得出各志愿评分。该模型不同于传统的层次分析评价模型,在此为了弥补传统层次分析的权值均由人为评定的,导致权值的赋予过于主观性这一不足之处,通过查阅不同文献,比较后得到部分权值。并用支配因素的数量对权向量进行加权修正,较客观的算出各个准则的权值。本模型也存在一定的缺陷,将不同准则权重之间的关系简化为线性关系。在本模型中,仍存在部分权值是由人为评定的,但由于数据有限,且考生意愿不明确,模型难免具有一定主观性。
参考文献:
[1] 赵文波.影响高考志愿填报的因素及成因分析[J].浙江师大学报,1998,21(2):99-104.
[2] 邓露.高考志愿录取概率的实用模型[J].科教文汇,2011,79(3):79-81.
[3] 姜启源.数学模型[M].北京:高等教育出版社,2011.
[4] 陆常辉.高考志愿录取概率模型研究[J].计算机工程与应用,2010,46(21):14-16.
[5] 马晓燕.高考志愿填报的层次分析模型[J].泰山学院学报,2003,25(6):9-12.
[6] 王智星.高考志愿预测的数学模型研究[J].电脑知识与技术,2016,12(10):94-98.
- 浅析当代服装设计的跨领域合作
- 浅谈数字技术对于舞台布景设计与制作的帮助
- 秦腔历史剧《司马迁》的创作分析
- 反抗与接受——《欲望号街车》中女性形象
- 《诗品·序》中的五言诗论
- 分析《无声告白》中畸形爱情的形成原因
- 浅析弗吉尼亚·伍尔芙的人生哲学在《海浪》中的体现
- 论《吃瓜时代的儿女们》的叙述手法
- 铜仁傩文化研究
- 试论《我不是药神》中的期待可能性
- 批判重商主义——《错误的喜剧》中基于信誉的经济共同体
- “汉语桥”中文比赛中华文化传播探析
- 少数民族地区青少年普通话推广传播受众分析
- “三化论”视域下的诗歌意象重构
- 基于价值链理论下我国传媒产业融合成因及生存路径分析
- 探讨中国创意产业的发展现状及问题
- 广告设计视觉语言的本土化研究
- 公益性网络自制综艺传播营销策略的浅析
- 以上党地区出土墓志为例观其中王书平民化现象
- 违反合作原则视角下的会话含义研究
- 刍议苏北新洋农场生态乡村建设现状
- “X+mate/友”复合词的对称性与不对称性
- 弗莱彻境遇伦理学三种道德选择方法下的安乐死问题研究
- 中日近代社会中的女性主义之比较
- 目的论指导下动词性隐喻翻译研究——以《红楼梦》中的“微笑”构式为例
- cherry-pick
- cherrypick
- cherry picker
- cherry-ˌpicking
- cherub
- cherubic
- cherubical
- cherubically
- cherubimical
- cherubinical
- cherublike
- cherubs
- chess
- chessboxer
- chesses
- chesses'
- chess's
- chest
- chest drawers
- chested
- chestfuls
- chestnut
- chestnuts
- chestnutting
- chest of drawers
- 用轻松的文笔,随随便便谈人生
- 用辞遣意
- 用过去的经验教训作为以后办事的借鉴
- 用过多的篇幅叙述
- 用运输工具装
- 用近似的事物来比照说明
- 用违其长
- 用途
- 用途广
- 用通俗的话解释
- 用通信方式讨要
- 用通条插到火炉里,把灰抖掉
- 用通讯仪器监督听取
- 用通讯设备传播的消息
- 用逸待劳
- 用遁形术隐藏身体
- 用道德加以引导,用礼教加以整治
- 用道理说服人
- 用邪术咒诅害人
- 用邮
- 用 部
- 用酒打猩猩
- 用酒泡制
- 用酒食待客
- 用酒食等慰劳