《基于遗传算法的旅游最优路径探究》-工学论文，计算机论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

基于遗传算法的旅游最优路径探究

范文

李振业陈婷陈静

摘要：旅游越来越成为人们喜爱的一种娱乐方式，但随着大量游客的涌入，各个旅游园区迫切需要设计合理高效的旅游路线提高游客的旅游质量。以徐州潘安湖风景区为例，采用遗传算法生成最优旅游路径，高效简单，能快速为消费者找到限制条件下的最优路径方案。

关键词：最优路径;遗传算法;旅游路线;数学建模

中图分类号：TP302? ? ? ? 文献标识码：A? ? ? ? 文章编号：1009-3044（2018）34-0181-03

1 问题描述

1.1 问题背景

随着徐州当地经济的发展，徐州潘安湖湿地公园游客不断增加，设计合理高效的旅游线路直接影响到园区的游客承受能力、广大游客的游览体验以及园区的经济效益等。

1.2 问题描述及假设

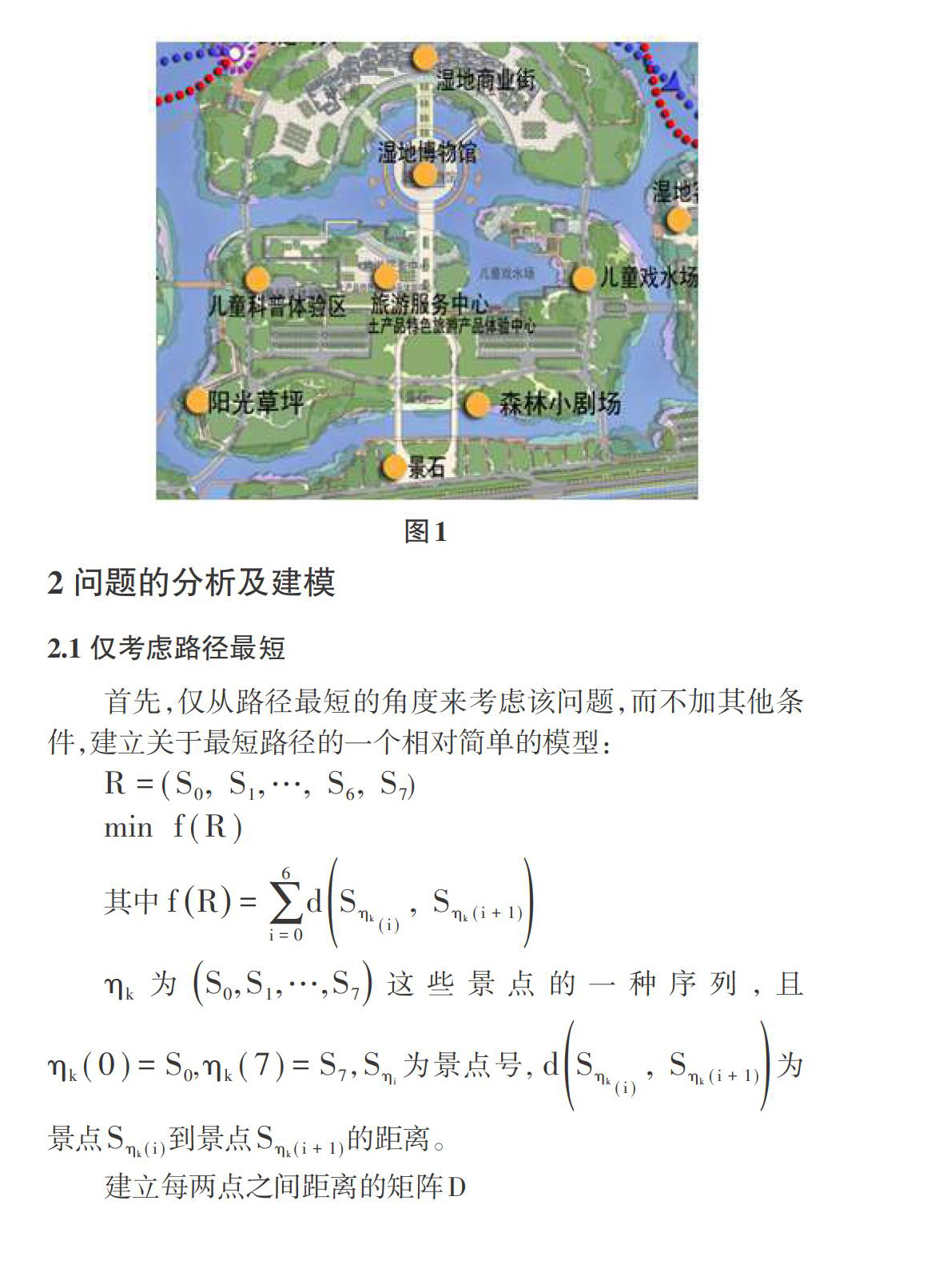
选取潘安湖景区的部分景点（如图1所示，每两景点之间往返距离已知）给出如下假设：

（1）各景点设置编号表示：S0：景石，S1：游客服务中心，S2：阳光草坪，S3：森林小剧场，S4：儿童科普体验区，S5：儿童戏水场，S6：湿地博物馆，S7：湿地商业街。

（2）任两个景点间存在最短步行距离分别为d（n1，n2）表示景點n1到景点n2的最短路径。

（3）假设游客的步行速度平均在2km/h左右。

（4）游客在景区停留的时间由“景点之间的步行时间”“景点游览时间（即在景点内游玩的时间）” 和“在景区外的等待时间”三部分组成，其他时间忽略不计。

有3个旅游团，12：00同时从景石出发，要求三个旅游团17：00前到达湿地商业街，17：30离开湿地商业街（注：?各景点限时开放?森林小剧场只在半点或整点开放;?湿地商业街游览时间至少为30分钟），并且每个景点（湿地商业街除外）同时只能容纳1个旅游团游览，按照时间顺序后到达的旅游团，需要等待先到达的旅游团游览结束之后才能开始游览。建立数学模型，为三个旅游团分别设计一条能游览完全部7个景点且游览总时间最长的游览路线。

3 结论

3.1 模型的优点

（1）计算简单，结果准确，符合实际，具有可行性;

（2）遗传算法具有系统优化、适应和学习的高性能计算，不需要求导或其他辅助知识，只需要适应度函数值。基于自适应搜索技术增加搜索过程的灵活性，具有较好的全局优化求解能力。直接以目标函数值为搜索信息，对函数的形态无要求，具有较好的普适性和易扩充性，更适合大规模复杂问题的优化。

3.2 模型的缺点

（1）约束条件少，具有理想化;

（2）节点变多会使计算量剧增;

（3）轮盘赌法策略可能会产生较大的抽样误差，如果产生异常个体引起早熟收敛，影响求得全局最优解，

（4）进化过程中产生大量数据，计算大、占用时间长。

3.3 模型的改进

（1）改变遗传算法的控制参数，控制参数一般有群体大小、交叉概率、变异概率等，它们对算法性能有很大影响。

（2）轮盘赌法可能产生较大的抽样误差，可选用改进方法，如非线性排名选择，基于局部竞争机制的选择等。

参考文献：

[1] 王法有，刘玉娟.通过数学建模设计四川11名景最佳旅游路线[J].数学学习与研究，2010（17）.

[2] 于莹莹，陈燕，李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策，2014，29（8）.

[3] 李波，秦华旺.路径优化案例遗传算法的实现[J].电子设计工程，2017，25（20）.

[4] 邓雪，李家铭.层次分析法在权重计算方法分析极其应用研究[J].数学的实践与认识，2012，42（7）.

[5] 常洪江.遗传算法综述[J].电脑学习，2016（3）.

【通联编辑：代影】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。