网站首页  词典首页

标题	核心素养背景下初中数学教学设计需要关注的基本问题
范文	吕井春 [摘? 要] 核心素养培育的背景下，作为教学过程的先行者，教学设计发挥着重要的作用. 关注数学方法、思维能力、问题驱动学生思维发展、预设与生成等基本问题，可以让数学教学设计更好地服务于核心素养的培育. [关键词] 初中数学;核心素养;教学设计;基本问题;平行四边形的性质 教学设计是教学蓝图规划的过程，是教师对学生学习过程的预设. 在传统的数学教学中，教学設计是围绕知识的达成与运用来进行的，课程改革之后，教学设计中多了对学习方式的体现，强调设计一些能够让学生自主、合作、探究的教学方式，以实现学生对数学知识的主动建构. 当前，我们面临的是一个核心素养的教学背景，面对新的教育教学目标要求，作为教学先行者的教学设计，应当如何进行呢？笔者以为要回答这个问题，需要对教学设计的一些基本问题进行关注，并给出符合核心素养培育需要的回答. 教学设计要体现数学方法与思维能力对核心素养培育的作用 教学设计包括的内容很多，包括知识层面，包括教学方式以及对应的学习方式，包括数学思想方法、数学思维以及促进学生思维能力发展的具体策略等. 在笔者看来，其中最为重要的两个支撑就是数学方法与思维能力. 尤其是在核心素养的背景下，这两者是支撑以“必备品格”与“关键能力”为基点的核心素养培育的基础;同时从数学学科核心素养来看，其涉及的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等，都需要具体的数学方法与思维来提供支撑. 当前，安徽地区初中数学使用的是沪教版教材，该教材内容设置合理，编排科学，能够较好地体现课程改革要求，也有丰富的能够服务于核心素养培育的素材可供发掘. 以“平行四边形的性质”为例，该内容的教学设计中，如何体现出数学方法与思维能力对核心素养的作用呢？笔者是这样思考的： 其一，提取知识生成背后的数学方法因素，并努力转换为学生的关键能力. 可以不夸张地讲，任何一个数学知识的生成，背后都有丰富的数学方法. 在沪教版教材中，平行四边形被定义为“两组对边分别平行的四边形”. 这个定义给出了平行四边形的基本特征，那就是“两组对边分别平行”，教学设计中，在根据这个定义发掘平行四边形的性质时，可以设计先采用逻辑推理的方法，让学生根据定义去判断一些图形是否为平行四边形（如图1）. 这么设计的依据是：根据经验，学生的思维会围绕定义中的“两组对边分别平行”这一论述来判断，判断过程中的主要思维方式是比较思维. 在比较的过程中，一些基本概念如对边、对角、邻角等也会自然出现，并且学生能够自主发现“平行四边形邻角互补”等性质. 教学经验表明，这个发现的过程是非常自然的，因为平行线的性质在此可以起到重要的促进知识生成的作用. 在此基础上，教师引导学生通过构建全等三角形的方式，还可以证明“平行四边形的对边相等”等，从而逐步发现其他性质. 分析这一学习过程，我们可以发现学生之所以能够顺利地发现平行四边形的性质，关键在于教学设计的过程中，教师关注了数学方法（包括一般意义上的分析法、归纳法，也包括数学范畴内的比较、逻辑推理、模型运用等方法），关注了学生的思维过程，因而学生可以通过自主努力来获得知识. 显然，这个过程中学生的能力形成是有保证的，而且这种基于数学方法与思维的能力，可以认为是核心素养所需要的关键能力. 其二，在知识发生的过程中强调数学思维的作用，并引导学生通过反思认识其价值. 数学思想方法与数学思维，是蕴藏于数学知识发生的过程中的，传统教学中教师只关注知识生成的结果，对知识生成的过程有所忽视，甚至有时还会通过压缩、简化知识发生过程的方式来节省时间，以让学生有更多的训练时间. 从核心素养培育的角度来看，这样的做法显然是本末倒置的. 最佳的做法应该是充分丰富知识的发生过程，让学生不仅能够展开学习，还能够在学习中有反思的机会以发现数学思想方法与数学思维的作用. 在上面所举的“平行四边形的性质”探究过程中，在学生顺利得出平行四边形的性质之后，教师有必要让学生思考“我们是通过什么方法得到平行四边形性质的？”或者进一步追问“为什么有的学生的方法是不行的（教师可以在巡视的过程中寻找类似的例子）？”这样的问题，常常可以促使学生思考自己的学习过程，并反思自己的学习策略. 这样的反思，常常是指向数学方法与数学思维的，其可以从学习策略甚至是元认知策略的角度，帮学生形成关键能力. 用切合需要的问题驱动学生在知识构建过程中发展思维 问题之于数学学习的价值是不言而喻的，初中数学教学中，要想真正培育属于学生自己的必备品格与关键能力，一个重要的途径就是通过问题来撬动学生的思维. 当然，这里有一个前提，那就是问题必须切合学生的需要，问题要出现在学生思维遇阻之处，或者是学生的认知失衡之时，这样既可以从学习动机处激活学生的探究欲望，还可以为后面的知识生成奠定基础. 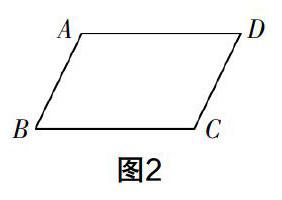比如说，在“平行四边形的性质”的探究过程中，得出“平行四边形的对边相等”这一性质的时候，教师通常都是根据题设去给出已知和求证：已知图2中的四边形ABCD，AB∥CD，AD∥BC，求证：AB=CD，AD=BC. 在解决这个问题的时候，通常是通过作对角线（如连接AC）的方式来构造全等三角形. 而这个辅助线一作，问题几乎就迎刃而解，因此这个问题解决的过程中，最大的难点其实存在于辅助线的构造上. 也就是说，学生此时关注的最大问题，其实不是连接了AC之后全等三角形的证明，而是怎么想到作这个辅助线的. 于是在教学设计中，笔者设计的就是教师在证明完毕之后，需要向学生提出问题：“在这类问题中，我们是怎么想到要作这条辅助线的呢？” 这个问题可以说问在几乎所有学生的需要之处——这个问题也是几何证明中最基本的问题，很多证明题难就难在辅助线的构造上，而此处提出这个问题，恰恰可以为学生解决此类问题奠定认识基础. 在这里，教学也因为这个问题的提出而有了一个新的天地，于是师生一起探究：我们要证明平行四边形对边的“数量”关系，也就是相等关系，而相等关系在几何中要么出现在等腰三角形腰的关系上，更多的则出现在三角形全等中. 此处显然是后者的思路，而图中又没有现成的全等三角形，那就需要去构造全等三角形. 显然，根据对图形的直觉性判断，连接对角线是最简单、直接的方法. 这种通过数学推理与数学直觉而建立的作辅助线的思路，常常是发展学生数学思维很好的途径. 而要打开学生的思维空间，问题的提出显然是必需的. 在上面的例子中可以肯定地讲，如果不是教师提出问题，或者说不是将学生自发生成的问题提出并放大的话，课堂上是不可能出现这种探究空间的. 因此，在数学教学中搜集、感知学生在知识发生过程中生成的问题，并在学生最迫切需要解决这个问题的时候讨论这个问题，就可以抓住教学契机，促进知识发生，发展学生的思维，从而为数学学科核心素养的培育奠定非常坚实的基础，因而这也是教师教学设计中要重点关注的问题. 教师的教学设计要适应学生在学习过程中表现出的变化 教学设计是教学实施的蓝图，是课堂教学的提前规划. 教学设计与学生的具体学习过程之间，是静态与动态、预设与实施的关系. 教学过程中因为学生的生成，肯定会出现教学设计与学生的学习过程不完全相同的情形. 这个时候就需要教师在教学设计的时候，预设好学生在学习中可能遇到的情形，并在实际教学中适应好学生的变化. 这是一个动态调整过程，考验的是教师在教学设计中能否准确预设到学生可能出现的情形. 通常情况下，教师的经验越丰富，越专注于学生学习过程中思维的展开，就越能准确地判断出学生的学习情形. 其实，在“平行四边形的性质”的教学设计过程中，笔者预设了这样的几种情形：一是学生想不到从边与角的角度去探究性质，二是学生想不到作辅助线，三是学生用来描述平行四边形性质的数学语言不准确. 针对这些问题，笔者预设的方案是：“形”的性质是要通过“数”去描述的，因此平行四边形的性质，必然是边或角的数量关系;辅助线的问题上面已经阐述，此处不再赘述;而描述平行四边形性质的语言，其实就是基于第一点的数量关系描述来确定的. 当然，在教学中也遇到了一些没有预设到的问题，比如有学生提出，如果一个平行四边形的四条边都相等，那就會有“更多的性质”. 显然，这个更多的性质是基于特殊的条件而得出的，这个时候教师最恰当的策略就是以表扬的方式进行评价：一方面肯定学生勇于探究的积极性;另一方面，从特殊与一般的角度界定平行四边形的性质，让学生知道平行四边形性质需要的是普适性而不是特殊性. 总之，在立足于核心素养培育的初中数学教学中，作为先行者的教学设计要瞄准核心素养培育的需要，立足于对基本问题的关注，这样才能为核心素养培育奠定坚实基础.
随便看	现代信息技术在“化学反应与化学平衡”专题教学中的应用 培养空间观念，学好立体几何 提高高中生数学解题能力的几点策略 实验探究“探究弹性势能的表达式” 浅谈政治课堂教学中公共参与素养的培育 初中信息技术课程教学中问题情境创设的策略 浅谈如何提高高中物理课堂教学的有效性 《日出东方白潮潮》的音乐解读与教学设计 高中政治材料题“答案组织形式”探究 STEM视角下的初中化学实验教学 高中物理教学中对物理二级规律的应用研究 初中数学教学中数形结合思想的应用 浅谈数学探究中思想方法的自我习得 浅谈高中数学概念的教学方法 谈提高初中物理课堂教学效率的几个做法 “比较”在初中化学课堂中的有效应用 初中英语阅读教学有效性的实践与探究 基于体验式学习下的“有机合成材料简介”教学 浅谈高中物理模块化教学策略 巧用学生资源打造高效思品课堂 通过“实验教学”培养初中生生物学科核心素养 艺术化导入在初中生物教学中的应用 让出精彩，引出新意 如何在初中物理教学中培养学生的科学探究能力 基于生态美学理念，教学“真学”生物 subcompensated subcompensates subcompensating subcompensation subcompensational subcompensations subcomplete subcompletely subcompleteness subcompletenesses subcompletion subcompletions subcomponent subcomponents subconcave subconcavely subconcaveness subconcavenesses subconcealed subconcession subconcessionaries subconcessionary subconcessions subcondensation subcondensations 摆开安排 摆开架势，准备作战 摆开阵势 摆弄 摆弄刀子发出响声 摆弄赏玩 摆式 摆张 摆当 摆忙 摆情况 摆战场 摆手 摆拉 摆拍 摆拍派人像摄影大师 摆拨 摆拽 摆挣 摆排场 摆搠 摆摆 摆摇 摆摊 摆摊儿

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。