网站首页  词典首页

请输入您要查询的论文：

　

标题 初中数学“学思课堂”的基本内涵及操作
范文 顾大权



[摘? 要] “学思课堂”基于我国古代教育家孔子的教育思想，在当代仍具有指导意义. 探索“学思课堂”的基本内涵和价值，能更好地体现新课标的要求和课程设计理念. “学思课堂”教学模式能改变传统教学的弊端，能扩大“学思课堂”产生的影响，能提高课堂教学效率.
[关键词] 学思课堂;基本内涵;模式建构
“学思课堂”的基本内涵
“学思”源自孔子的“学而不思则罔，思而不学则殆”，出自《论语·为政》，解释为：如果只学不思，即学习不经过思考便加以分析、整理、引申、归纳，所学虽多，也必然茫无所得;如果只思不学，一天到晚冥思苦想，思之虽勤也只能是空想，毫无用处. “学”是“思”的基础，“思”是“学”的升华，两者兼得就能将所学的知识进行归纳整理，重新建构，把复杂的知识系统化，从而把握住知识的核心，达到举一反三的效果.
学思课堂倡导“学”和“思”. “学”是主体，在教师问题的引导下，学生合作探究，交流讨论，主动学习;“思”为主线，“思”贯穿学习的整个过程，在学习的过程中注重思考. 只有思考，才能启迪学生的思维，才能发展学生的智力，才能提高学生的能力，才能培养学生的素养. 學思课堂主张“温故、知新、学思、笃行”，源自我国伟大的教育家孔子，这里的“学思”是指，从学生熟悉的知识经验入手，学生在合作探究中发现新知识、习得新经验，通过巩固、强化，达到知识的理解、迁移甚至创新;在思考总结中掌握数学思想方法，积累数学活动经验，发展数学核心能力，培养数学创新精神.
“学思课堂”的核心价值
学思课堂与传统的课堂教学相比，强调学生主动“学”，即由传统的教师“教”的课堂变为学生主动“学”的课堂，学生的学习方式彻底改变了，此时学生是学习的主人. 课堂中要培养学生的自主学习能力、合作学习能力和探究学习能力，“微探究”是主要的手段. “微探究”能让学生发现问题、提出问题、分析问题和解决问题，能让学生经历知识发展、完善的过程，经历真正的思维活动. 学思课堂另一方面是强调学习过程中的“思”. 在情境导入环节，教师可设置符合学生实际的恰当情境，让学生思考后找到新旧知识的联结点，弄清知识产生的来源，使学生对知识的产生“知其然，更知其所以然”;在知识生成环节，学生通过思考，可以“发现”知识，掌握数学研究的思路和方法，积累数学活动经验，发展创新能力;在知识巩固环节，学生通过思考、讨论，可以加深对知识的理解，达到知识的迁移和创新，掌握数学思想方法，提升数学思考能力和解决问题的能力.
“学思课堂”的模式构建
学思课堂基于孔子的教育思想和心理学学习认知理论、建构主义理论和多元智能理论，主要由“温故”“知新”“笃行”三部分构成，“学思”则贯穿这三个环节.
温故环节教学目标的制定要面向80%左右的学生，“故”的设计要符合学生的“最近发展区”. “故”可以是学生已有的知识，也可以是学生的经验，这个经验包括学生的生活经验、活动经验和思考经验. 温故的过程要符合学生的认知规律，“故”的设置要适合后面的探究学习，要考虑知识产生的背景，知识形成的来龙去脉，以及知识形成过程中所渗透的思想方法和积累的活动经验.
知新环节是在温故的基础上经历观察、猜想、交流、验证等学习活动生成新知. 探究生成是知新环节的主要特征，“微探究”是知新环节的主要手段. 知新的过程通过探究学习得到，比接受学习得到的更为印象深刻. 在探究的过程中，教师要适时进行诱导、启发，真正成为探究学习的组织者、参与者、合作者和课堂气氛的营造者. 教师要把握启发的时机，避免学生失去“发现”的机会，也要避免学生长时间处于无助状态. 知新的过程要体现学生的主体地位，重视教师的主导作用，要让学生掌握研究数学问题的思路和方法，积累数学研究的活动经验，体现数学课程的设计理念，提升学生的数学素养.
笃行环节是在知新的基础上，通过巩固、强化等来理解新知识，掌握新知识. 笃行环节要体现双80%的要求：例题的设置要面向80%左右的学生，要保证学生能掌握80%左右的核心知识. 例题、练习题的设计要有针对性，要有利于强化学生对新知的掌握. 试题应能让学生对新知加以辨析，避免可能发生的错误，应能强化学生对新知的理解，积累学习经验. 例题、习题的目标定位要准确，针对性要强，要体现出其应有的价值，要发挥出其在教学中的作用. 在新知巩固的过程中，我们要发展学生的思维，提升学生的能力，培养学生的数学创造精神.
学思贯穿课堂的每一个环节. 通过思考，学生能找到新旧知识的联结点，弄清知识产生的来源，能在已有知识基础上生长出新的知识;通过思考，学生能辨析新知，弄清新知形成的思路方法，学会数学地思考;通过思考，学生能掌握解决一类问题的通识通法，能掌握解决问题的核心.
“学思课堂”的典型案例
下面以义务教育数学教材九年级下册“7.1 正切”的教学设计为例，谈谈“学思课堂”的教学流程.
（一）教学内容分析
正切是函数的延续，它揭示的是角度与线段比值之间的对应关系，是用符号表示的一种函数，是直角三角形中角与边之间关系的进一步探究. 正切概念的建立是本节课的重点. 正切是初中阶段学习的第一个三角函数，我们要让学生经历、感悟、体验正切的切入点、正切的形成和正切的应用. 本节课作为章节的起始课，起着承上启下的作用，一方面承接函数，另一方面，其能为学习正弦、余弦积累经验.
（二）学情分析
初三的学生已经具备一定的学习能力，但理性思维的方法、习惯和深度都不够完善. 在以前的学习中，学生已了解了直角三角形的边、角关系，并掌握了相似三角形的相关知识，具备一定的抽象、概括和归纳能力. 在本节课的教学中，教师可通过生活实际问题引导学生独立思考、合作交流，并归纳出所观察现象的本质特征，总结出有价值的理论知识，从而获得正切函数的概念.
（三）教学目标
1. 理解正切的概念;会在直角三角形中求出某个锐角的正切值;了解锐角的正切值随锐角的增大而增大，能用正切的知识解决实际问题.
2. 经历操作、观察、思考、求解等过程，感受数形结合思想方法，培养学生的理性思维.
3. 激发学生的学习积极性和主动性，引导学生自主探索、合作交流，培养学生的创新意识.
（四）教学重难点
重点：理解正切的概念，会在直角三角形中求出某个锐角的正切值.
难点：理解正切的概念，体会函数思想.
（五）教学过程
1. 温故
在日常生活中，我们经常走台阶，有的台阶走起来比较吃力，有的台阶走起来却比较舒服，这和台阶的陡峭程度有关.
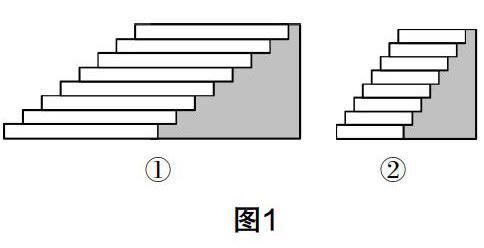
问题1？如图1，下面两个台阶哪个更陡？你是怎么判断的？
设计意图？让学生根据生活经验，得到台阶的陡峭程度由倾斜角的大小决定：角度越大，台阶越陡. 如图1中台阶的陡峭程度，可转化为看图2中两个角的大小，显然57°>38°，所以图1中的第2个台阶更陡.
问题2？?如图3，哪个台阶最陡？你是如何判断的？
设计意图？摇 引导学生发现台阶的陡峭程度还可以由台阶的竖直高度与水平长度的比值来决定：比值越大，台阶越陡. 由此发现台阶的陡峭程度既可以由台阶的竖直高度与水平长度的比值决定，又可以由台阶的倾斜角的大小决定. 那么，这两者之间存在一定的联系.
问题3？摇如图4，哪个台阶更陡？你是如何判断的？
设计意图？摇 引导学生发现台阶的竖直高度与水平长度的比值相等时，台阶的倾斜角的大小也相等，此时台阶的陡峭程度是一样的.
2. 知新
问题4？如图5，∠A的大小不变，竖直高度和水平长度的比值是否发生变化？
一般地，如果锐角A的大小确定，我们可以作出无数个含有∠A的直角三角形：Rt△AB1C1，Rt△AB2C2，Rt△AB3C3?…（如图5）.
观察、思考并归纳、小结，可以得到Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3…根据相似三角形的性质，得B1C1/AC1=B2C2/AC2=B3C3/AC3=…
也就是說，如果直角三角形的一个锐角大小确定，那么这个锐角的对边与邻边的比值也确定.
设计意图？摇 让学生在交流讨论中发现锐角的大小确定，台阶的竖直高度与水平长度的比值也确定，所以倾斜角的大小和台阶的竖直高度与水平长度的比值之间确实存在一种关系.
正切的定义：如图6，在Rt△ABC中，∠C=90°，a，b分别是∠A的对边和邻边. 我们将∠A的对边a与邻边b的比叫作∠A的正切（tangent），记作tanA，即tanA=∠A的对边/∠A的邻边=BC/AC=a/b.
你能用同样的方法写出∠B的正切吗？
设计意图？摇 学生发现锐角和竖直高度与水平长度的比值存在一定的关系后，迫切地想找到这种关系，此时便可顺理成章地提出正切的概念，开启学习新知的大门.
3. 笃行
例1？如图7，在Rt△ABC中，∠C=90°，AC=3，AB=5，求tanA，tanB.
设计意图？摇 让学生通过具体的问题求正切值，起到强化、巩固正切定义的目的.
练习？?如图8，求出图形中各锐角的正切值.
思考：通过计算tanA，tanB的值，你有什么新的发现？
设计意图？摇 图形①②用于学生继续巩固正切的概念，同时引导学生发现互余两角的正切值互为倒数. 图形③是让学生通过构造直角三角形求正切，学生通过不同的构造方法会发现，锐角的正切值和三角形的大小无关，只和锐角的大小有关.
变式？?如图9，在Rt△ABC中，AC=3，AB=5，CD是AB边上的高，求∠ACD和∠BCD的正切值.
设计意图？摇 除了根据条件直接求正切值而外，还可以将所求的角转化为与其相等的角，通过求等角的正切值来解决;也可以转化为余角，利用互余两角的正切值互为倒数解决，从而渗透转化思想方法.
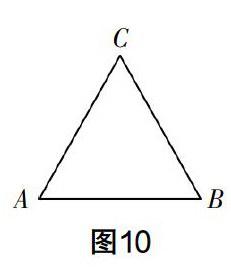
例2？?如图10，在等边三角形ABC中，AB=2，求tanA.
通过计算tanA的值，你对60°角的正切值有什么认识？30°角呢？你还能得到其他的吗？
设计意图？摇 先构造直角三角形再求正切值，可同时得到两个特殊角的正切值，此时能让学生感知到，锐角增大，正切值也增大.
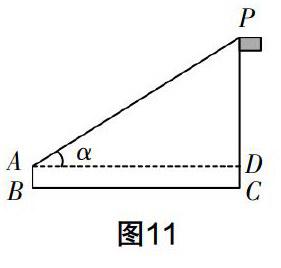
例3？摇 如图11，周一升旗仪式上，身高1.5米（眼睛距地面）的小明站在离旗杆30米处，一直注视着国旗冉冉升起，小明的视线与水平线的夹角为α.
（1）若旗杆高为21.5米，当国旗升到顶部时，求∠α的正切值.
（2）在升旗的过程中，∠α的大小在不断变化，此时∠α的正切值在变化吗？试探究.
发现：锐角α的正切值随着α的增大而增大.
设计意图？摇 （1）继续强化利用定义直接求锐角的正切值;（2）让学生知道一个α的值，就对应一个α的正切值，渗透正切函数思想，同时利用升旗过程让学生发现锐角的正切值随着角度的增大而增大.
4. 学思
（1）本节课你学习了哪些知识？
①理解锐角的正切的概念，知道在直角三角形中，锐角的正切与两直角边之间的关系.
②会根据图形或条件求一个角的正切值，有时要通过构造的方法求正切值.
③知道锐角的正切值随着锐角的变化是如何变化的.
（2）思考延伸
本节课我们发现直角三角形中一个锐角的大小确定，那么这个锐角的对边与这个角的邻边的比值确定，我们称这个比值为正切. 那么，这个直角三角形中锐角的对边与斜边的比值是否也确定呢？任意两边的比值是否确定呢？请有兴趣的同学继续探究.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 22:44:25