网站首页  词典首页

标题	运用待定系数，解决抛物线问题
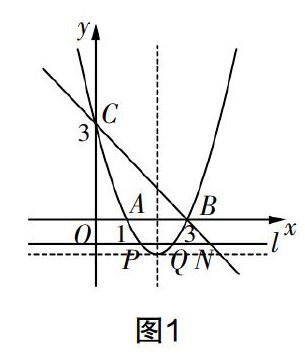
范文	陈朝建 [摘? 要] 在中考中，与函数相关的题型是中考考查的重点内容，而在函数问题中，曲线（抛物线和双曲线）问题考查的次数尤为频繁. 应该如何解决这些问题呢？笔者认为，采用待定系数法是解决这类题型的首选方法. [关键词] 待定系数;曲线;函数 待定系数法是解决曲线（抛物线和双曲线）问题的经典方法，通过将已知条件代入曲线方程，可以得到相关的方程，只要求出未知系數，曲线的表达式自然能够求出. 本文中的例题选用了近三年的中考真题及模拟题，以让学生更好地理解和掌握待定系数法. 试题呈现与思路点拨 试题? （2017年湖北武汉中考模拟题）在平面直角坐标系中，二次函数y=mx2-2mx+m-1（m>0）与x轴交于A，B两点，顶点为C，将抛物线在A，C，B之间的部分命名为图像E（不包含A，B两点）. （1）计算二次函数的顶点坐标. （2）当AB=6时，直线y=kx+b经过点C，且与图像E有两个交点，请求出k的范围. （3）当m=1时，求线段AB上的整点个数;若图像E与线段AB围成的区域整点数为6个（包括边界），试着求m的取值范围. 反思? 本题属于平面直角坐标系中的二次函数相关题型，对于问题（1），属于基础题型，通过将二次函数解析式配方，即可得到顶点坐标. 问题（2）属于两图形有交点，求未知数范围的问题，解题过程如下：根据题意可求出A，B的坐标，结合点C的坐标，可以分别求得直线AC和直线BC相对应的k值，再数形结合，即可求出k的范围. 问题（3）属于本题的升华，也是学生拉开分数的一问，应采用待定系数法求解. 问题（3）的前半部分很简单，令y=0，解方程便可求得A，B两点的坐标，于是可轻易求出满足条件的整点个数;通过前半部分的引入，后半部分很容易解决——首先令y=0，求得A，B两点的坐标（用含有m的代数式表示），然后根据整点的个数，列出关于m的不等式，解不等式即可. 巩固延伸 反思? 本题属于待定系数法与平面几何相结合的综合题，求解过程都是从平面坐标入手，实现几何元素的参数化，结合几何性质，利用代数分析求解收尾. 解决此类问题时，要善于运用待定系数法，并数形结合，以形助数. 总结提高 2. 初中数学中的曲线问题属于重点内容，运用待定系数法解决曲线问题可以起到事半功倍的效果. 虽然曲线问题的解法多种多样，但待定系数法是最基本的方法. 万丈高楼平地起，只有掌握基本的解题方法，才能探索更多的技巧性知识. 许多学生对一些基本的问题不屑一顾，认为这些问题非常简单，但这属于明显的眼高手低，只有真正去做，通过不断的练习，才能从根本上掌握这些知识. 3. 对于一些函数问题，往往需要结合函数图像才能更好地解决. 本文中的拓展题就用到了数形结合思想——通过题目所给的条件，可精准地画出函数图像，结合函数图像可以将抽象的问题具体化. 从函数图像中可以明显地发现对称性，而拓展题的关键就在于此. 数形结合是初中数学中的基本方法，学生在平时的学习中应加以重视，要学会从几何的角度去思考代数问题，做到数形结合，以形助数.
随便看	释放内心——浅析现当代艺术家的心理发展历程 浅谈水彩画创作中的“神遇” 论中国风景油画的意境之美 中国传统纹样与西方波普艺术及对两者结合的探究 浅析近代画家陈少梅 中国乡土现实主义创作回顾（1980—1984） 浅谈青花纹饰的演变过程 林容生工笔山水画的色彩研究与应用 图形创新与综合应用 浅析黑白装饰画的艺术表现 浅谈对水彩的认识 田世光工笔花鸟画双勾重彩技法分析与借鉴 徽州建筑的色彩之美 山东大学（威海）印象——文心湖优劣评述 浅析魏晋玄学与中国古典园林 水彩画中“水”的艺术表现力 浅谈水彩艺术抽象意味的特殊性 根雕艺术中蕴含的生态美学特征分析 浅谈当代油画讽刺元素的表现 中世纪早期罗马式建筑艺术分析 “大地艺术”的观念与实践研究 《群山之巅》中底层小人物的命运书写 《名优之死》在女性自由视角下的解读与反思 论鲁迅小说中的新知识分子形象 从明清“剪灯戏”看《剪灯新话》的戏曲改编 tomato tomatoes tomatoey tomb tombal tombed tombic tombing tombless tomblike tomboy tomboyish tomboyishly tomboyishness tomboyishnesses tomboyism tomboys tombs tombstone tombstoner tombstones tomcat tomcats tomcatted tomcatting 饥饱不时 饥饱劳役 饥饱劳碌 饥饿 饥饿中的百姓处境困难，亟待救助 饥饿之徒 饥饿乱离 饥饿劳累 饥饿劳苦 饥饿困乏 饥饿困乏的样子 饥饿困厄 饥饿困病 饥饿困窘 饥饿困顿 饥饿寒冷 饥饿时的肠鸣声 饥饿时腹鸣有声 饥饿是各门工艺的老师 饥饿求食的样子 饥饿流离 饥饿疲乏 饥饿疲乏，灰心失意 饥饿疲倦 饥饿疲惫

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。