网站首页  词典首页

标题	精化设计方案，有序推进教学
范文	刘剑和 [摘? 要] 有理数的乘法运算在有理数的运算中起桥梁作用. 对于该内容的教学，需要精化设计教案，使学生在良好的课堂氛围中获得知识和能力的提升，本文将结合课堂教学“四化”原则开展教学探讨，与同行交流. [关键词] 有理数;乘法;运算;情境化;链式化;讲评 “有理数的乘法”是苏科版七年级上册的重要内容，新课标明确指出要让学生掌握有理数的乘法运算，理解有理数乘法的运算律，并能够应用运算法则解决问题. 基于上述课标要求，笔者将根据教学“四化”提出“有理数的乘法”教学的几点建议. 课堂教学情境化，提升学生兴趣 新课程理念强调要重视学生在课堂教学中的主体地位，要充分调动学生的学习兴趣，让学生在丰富的活动中完成知识的过渡、理解和深化，即开展情境化教学. 同样的对于知识跳跃性较大的有理数乘法也需要遵循该理念，利用丰富的生活实例、数学材料，创设与学生生活相贴切的活动来调动学生的知识储备和学习兴趣. 情境化教学的重点是“趣味”和“实效”二字，前者活跃气氛，后者指明实用原则，包括材料的实际价值和内容的思考价值. 考虑到有理数乘法与加法相关联的本质，在情境教学的引入阶段可以借用与加法运算相关的问题，从具体的生活问题中抽象乘法的概念，使学生逐步由感性认识上升到具体的理性理解. 如教学中给出如下两个情境问题： 问题1：A地区近来连降大雨，水库水位连续升高，若每天升高3 cm，则4天后水库总的水位变化量是多少？ 加法：3+3+3+3=12 cm;乘法：3×4=12 cm. 问题2：B地区近来干旱，水库水位连续下降，若每天下降3 cm，则4天后水库总的水位变化量是多少？ 加法：（-3）+（-3）+（-3）+（-3）= -12 cm;乘法：-3×4=-12 cm. 将生活中常见的水位变化问题作为有理数乘法的教学引入，学生可以充分感知生活中的数学，体会数学学习的乐趣. 而材料的设计并不是随意的，而是考虑到学生的认知水平，选用了与加法相关的问题，在实际教学中可以适时地引导学生思考上述两个问题如何用算式来表示. 但需要注意的是情境化材料不能代替数学的归纳法则，而应以情境材料作为数学法则的抽象依据，设定合理的数学规则，完成法则的归纳. 如上述问题就可以设定当天的水位线为0，水位上升为正，下降为负，基于此规则进行有理数乘法模型的初步构建. 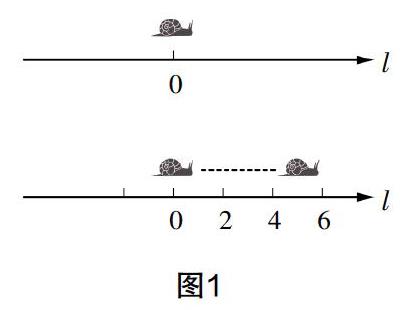同时也可以考虑采用更具直观性和数学化的数轴，如给出如下更具数学意义的趣味问题： 假设一只蜗牛沿着直线向右爬行，如图1，若令数轴的点O作为蜗牛的出发点，当蜗牛以2 cm/分钟的速度向右爬行时，试分析1分钟、2分钟、3分钟后蜗牛所处的位置;若其他条件不变，蜗牛的爬行方向修改为“向左爬行”，再次分析1分钟、2分钟、3分钟后蜗牛所处的位置，试用数学式表示. 上述情境问题的特点是将情境问题与数轴相结合，完成了生活实例向数学问题的抽象，而利用数学式表示则是数学模型构建的过程. 从上述问题的构建思路可以看出情境问题设计的目标指向性，既调动了学生的兴趣，又实现了概念、法则的形象化，学生的思维得到了碰撞，获得了一定的启发. 环节推进链式化，提升学生能力 本节课的主要任务是让学生掌握有理数乘法的法则，相对而言，时间短任务重，这就要求教师在教学环节设计上要循序渐进、环环相扣，预设合理的问题引发学生的思考，然后采用活动探究的方式，让学生体验探究的过程，自然而然地获得知识与能力的提升. 之前我们探究过有理数的加法，本节内容我们可以沿用“提出假设→情境问题→模型构建→归纳结论”的设计模式，并采用问题驱动的方式推进环节. 如环节一，提出假设，考虑到有理数乘法与加法有相似之处，均可以分解为符号变化和绝对值运算两部分，因此在该环节就可以类比加法法则，让学生思考有理数乘法中的符号和绝对值如何变化. 问题可设计为：有理数的加法法则包括符号和绝对值两部分，那么有理數乘法的符号和绝对值是如何变化的，是否存在类似的规律？第二环节的“情境问题”则需要设计螺旋上升的问题，从生活中的实例抽象为数学问题，主要任务是促进学生思维的开化，问题设计则应在注重趣味性的同时兼具实用性. 上述最为重要的是第三环节的“模型构建”，该阶段需要引导学生从实例问题中抽象数学模型，最为有效的方式是结合数学的数形结合思想和模型思想. 问题设计上应紧扣环节一关于乘法法则的符号和绝对值，将生活问题符号化、数值化，利用问题引导学生对算式进行分类，关注算式中符号和绝对值的变化. 最后的“归纳结论”环节则是对运算规律的理论升华，需要注意的是该环节不能直接由情境问题来进行法则归纳，而应给出众多的数学算式，引导学生对算式进行计算、分类、比较，给学生留足思考的空间，逐步完成法则归纳. 还要注意引导学生关注法则中的特例，如与零相乘的情形，确保法则的完整性. 遵循学生的认知规律，以学生为主体的链条式教学环节设计更能激励学生探索未知，思考数学，同时也是知识衍生发展和数学思想相融合的智慧教学方式. 学生的思考比较、类比抽象和概括总结能力也会得到显著的提升. 课例讲评全面化，提升学生逻辑力 运算法则是一种规律性强、内容较为抽象的数学算法，在课堂教学中即使学生有一定的领悟也很难快速形成自己的认识，更难以直接转化为应用法则，此时就需要教师结合具体的题目，采用分步讲解的方式引导学生深刻认识法则，构建自己的解题框架. 巩固设计多样化，促进学生反思 对于学生而言，有理数的乘法运算较为烦琐，存在法则理解上的困难，因此教学的最后环节需要设计一定的巩固练习题，用一定的运算量来帮助学生巩固知识，确保学生的学习质量. 同时在设计时需要注意题量适中，以题型互补、思维调节为设计核心，让学生在解题的过程中获得知识的关联和自然生长. 另外在每个小题之后应适当编排思考题，引导学生思考解题过程，总结解题经验. 如设计如下问题： 思考1：问题中含有分数时需要注意哪些事项？分数参与运算的算式，在计算时的具体步骤是什么？ 思考2：对于有字母参与的乘法算式，你有哪些经验？对于较为复杂的乘法算式，在确定符号时你有哪些经验可供分享？ 将问题与思考相结合有利于引导学生总结解题过程中的经验，培养学生的逻辑思维，帮助学生形成自己的解题策略，这才是巩固练习设计的意义所在. 而在巩固设计中采用“基础练习→关联练习→拓展练习”的模式则可以充分锻炼学生的思维，培养学生思维的开放性和拓展性，使学生的解题层次获得提升. 总之，数学的教学应是引导学生掌握知识、数学思维获得提升的过程. 按照“双基”的发展要求，要让学生“学会数学”的同时“会学数学”，即不仅掌握知识，还要提升能力，该教学思想同样适用于“有理数的乘法”，而后者的能力提升才是课堂教学的核心所在，也是学生长远发展的根本所在.
随便看	伤在心上，感在身上 先定两端，后编中间 “寻人启示” 孩子在成长 送你一朵勿忘我 入情入境，合情合理 开发精准写作知识是写作教学的关键 Ⅲ“多角度展开景物描写”课堂实录 Ⅱ“校园奇人：抓特点，写精神”课堂实录 写作教学工作要有一种专业自觉 I“以声塑人，声入人心”课堂实录 和学生的心弦对准音调 让“三新”思想在课堂里开花 读你，精神成长中的追梦人 挤出来·流出来·涌出来 真实是创作的灵魂 7、8合刊 将“凝视”进行到底 三步法，提升语言表现力 谈记叙文写作构思的步骤和方法 中考作文命题的四重追求 以趣带写，激发能动学习 也谈批判性思维的培养 “三度”绘场面，精彩在细微 认识“莲道”三个“一”：比类读，比类行 holding-on holding on holdingoperation holding opeˌration holding-out holding out holdings holding together holding up hold it against hold/keep sb in custody hold/keep sth in check hold-off hold off hold office hold off (sth/doing sth) hold on hold-on hold on/hang on hold on / hold onto sb/sth hold onto hold on to hold on to/hang on to hold onto sb/sth hold on (to something/somebody) 鞉鞞 鞉音 鞉鼓 鞉鼓的旁耳 鞋 鞋、袜 鞋不加丝，衣不加寸 鞋不增分，衣不增寸 鞋不让分，衣不让寸 鞋刷 鞋刷子脱毛 鞋匠 鞋匠只应守鞋楦 鞋口 鞋合穿 鞋后跟 鞋和衣带 鞋城 鞋壳篓子 鞋头 鞋头上刺花 鞋子 鞋子光剩下帮——没底 鞋子合脚走得快 鞋子在什么地方挤脚唯有穿鞋的人明白

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。