网站首页  词典首页

标题	让学生感受活灵活现的数学
范文	[摘 要] 优质的数学学习离不开灵活多变的思维支撑. 因此，不断将知识内容，特别是基础知识以变形创新的方式加以呈现，已经成了当前高中数学教学的首选之法. 笔者通过对相关教学理论进行研究，结合高中数学知识特点，以不同内容为界，总结出了若干知识变形途径，旨在为数学教学增添活力，提升實效. [关键词] 高中数学；基础知识；变形；推广；途径 灵活性是高中数学的一个突出特点，它既是数学学习的魅力所在，也是知识接受的难点体现. 对于这把双刃剑，如果能够处理好、运用好，将会成为教学实效提升的重要契机. 体现高中数学的灵活性，切入点有很多，其中思路最为清晰的一个方式就是从基础知识入手，对之进行变形与推广，引导学生从中发现灵活元素之所在，从而将数学学习推向新的高度. [?] 立足函数知识，开展变形推广 函数并不是高中阶段的学习特例，而是在整个数学学习过程当中都有所渗透与贯穿. 函数不仅仅是一个独立的知识内容，更是一种分析方法与思维方式. 因此，对于函数知识进行灵活变形，在促进高中数学学习的整体效果中便显得尤为关键. 例如，在对函数图像的内容进行学习时，笔者曾经要求学生完成这样一个问题解答：请通过配方的方式，找到函数f（x）=-3x2-6x+1的对称轴方程与顶点坐标，并确定其单调区间与能够取得的最值. 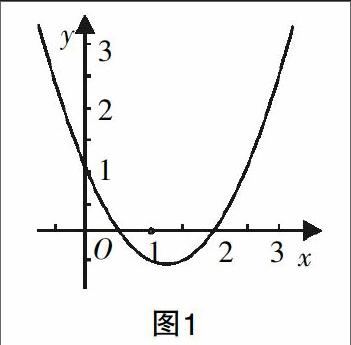为了让学生能够将图像这个基础知识掌握到位，笔者以这个内容为基点，对提问进行了变形：在二次函数f（x）=ax2+bx+c中，f（x1）=f（x2）（其中x1≠x2），则f 的值是多少？为了将知识要点体现得更加明确，笔者又将问题继续变形成为：在函数f（x）=x2+px+q中，对于任意的x都有f（1+x）=f（1-x），则f（0）， f（-1）与f（1）之间的大小关系如何？最后，笔者还为学生设计了这样一个问题：如图1，其所表示的是函数f（x）=ax2+bx+c的图像. 那么，能否尽可能多地将关于a，b，c的正确结论找出来？这些问题虽然彼此不同，却都是很明确地指向了函数图像这个基础知识要点. 通过问题的不断变形，学生对于这个内容的理解把握也更加深入了，真正体会到了图形的有效运用对于函数问题分析解答的重要意义. 函数领域的知识内容多种多样，根据不同的函数形式，可以拓展出不同的变形路径. 函数知识的这一特点也为基础知识的变形推广提供了十分广阔的空间. 如果对每种形式的函数都能够进行这一灵活探究，必然可以将学生的函数思想不断地夯实、提升. [?] 立足向量知识，开展变形推广 向量知识是学生进入到高中阶段之后才逐步开始接触的. 表面看来，向量内容的理解与应用似乎并不困难，但如果对这部分知识进行灵活变形，便能够清晰地意识到，其背后所隐含的挖掘空间是十分巨大的. 例如，在对平面向量的内容进行教学时，它的线性运算一直是一个基础且重要的知识部分. 为此，笔者在课堂教学中围绕这个知识内容设计了一系列变形问题. 问题1：如图2所示，四边形ABCD是平行四边形，且=a，=b，则应当如何用a，b来表示向量？问题2：如图3所示，在五边形ABCDE中，=a，=b，=c，=d，则应当如何用a，b，c，d来表示向量和？问题3：如图4所示，若四边形ABCD是平行四边形，且=a，=b，=c，=d，则在a+b+c+d=0，a-b+c-d=0，a+b-c-d=0，a-b-c+d=0四个结论中，正确的是哪一个？问题4：若a，b是两个非零向量，那么“ ”是“（a+b）与（a-b）”垂直的什么条件？问题5：在四边形ABCD中，=a+2b，=-4a-b，=-5a-3b，且a与b不共线，则该四边形的形状如何？从大体结构上来看，上述每个问题之间都是存在着相似之处的，但看似细小的变形却对学生提出了不同的解答要求. 随着问题变形的不断推进，向量运算的各个知识角度都得到了考查. [A][B][C][D][A][B][C][D][E][A][B][C][D][图2][图3][图4][O] 不难发现，向量知识的学习是十分需要关注细节的. 虽然只是对题目当中一些微小之处予以改变，其所对应的分析方向和解答方法却是完全不同的. 这也对向量基础知识的学习提出了要求. 以题目变形的方式强调知识细节，对于有效的基础知识学习来讲助益颇多. [?] 立足三角知识，开展变形推广 谈到三角知识，学生所想到的大多是单一的计算公式. 其实，在这些枯燥的理论知识之余，三角知识的应用路径也是极其广泛的. 即使知识内容再基础，也能够在实际问题的解答当中发挥出十分重要的作用. 而这也为基础知识的变形推广提供了入口. 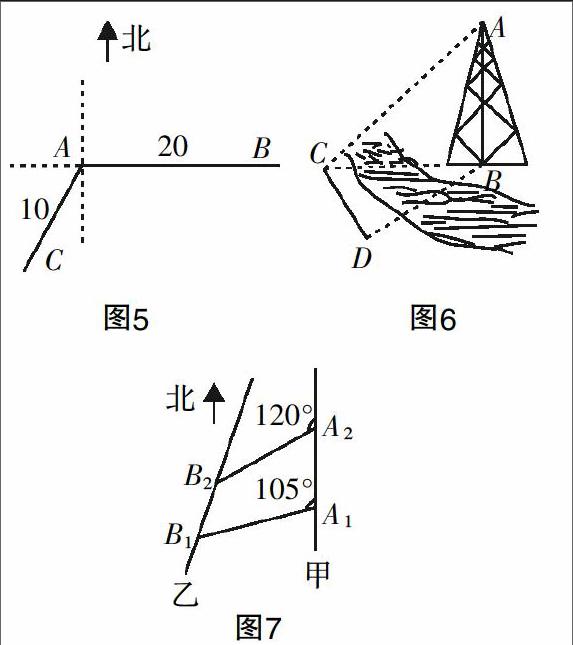例如，为了引导学生理解三角的知识内涵，笔者请学生依次完成下列实际问题的解答. 问题1：如图5所示，小船甲航行至点A时被告知要前往点B，其位于点A正东20海里处. 甲立刻出发，并通知了位于点C的小船乙一同前往，乙位于甲的南偏西30°10海里处. 那么，小船乙需要将航行方向确定为北偏东多少度（精确到1°）？问题2：如图6所示，某人站在河岸一侧，想要测量位于河对岸的铁塔AB的高度. 他先选择了与铁塔底端B位于同一水平面内的C，D两点，并测量出∠BCD=α，∠BDC=β，CD=s，且铁塔顶端A在点C处的仰角是θ，则能否确定出铁塔AB的高度？问题3：如图7所示，小船甲沿正北方向航行，速度为30海里/时，小船乙同样在固定方向上进行匀速航行. 当甲航行至A1时，乙到达B1，且位于甲的北偏西105°，相距20海里. 20分钟后，甲航行至A2，乙到达B2，且位于甲的北偏西120°，相距10海里. 则小船乙的航行速度是多少？在这样的实际问题解答过程中，学生反复运用了正余弦定理等基本方法，于无形之中夯实了基础. [A][B][C][北][A][B][D][C][20][图5][图6][10][北][A2][A1][B2][B1][甲][乙][120°][105°][图7] 师生们总会认为，基础知识的学习就是停留在理论层面的，也必然是单调枯燥的. 通过上述示例当中的实践，发现并不如此. 在开始接触基础知识时，便可以加入实际应用的元素，借助生活问题的解答，强化知识理解，夯实基础构建. 将三角知识进行这样的灵活变形，不仅拓宽了知识理解路径，还从一开始为学生增加了不少学习兴趣. [?] 立足数列知识，开展变形推广 数列是被学生所公认的难度较大的知识内容. 当数列问题以灵活、复杂的面貌呈现出来后，学生便总会感到无从下手，不知道该如何进行分析思考. 归根结底，这还是知识基础不够牢固的原因所导致的. 如果教师能够在基础知识教学阶段便将知识加以变式，必然能够为接下来的有效学习提供不小帮助. 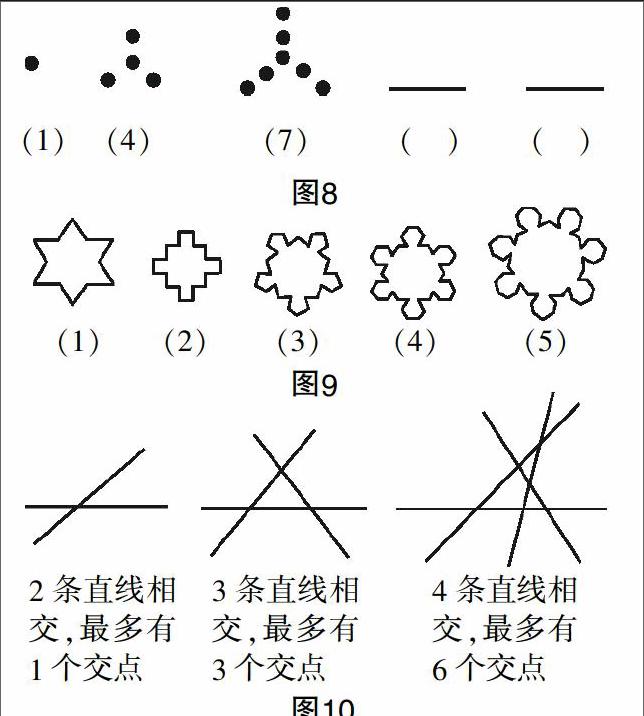例如，数列的通项公式是一个非常重要的基本概念，理解并求解通项公式也是数列问题当中第一个重要组成部分. 除了根据公式进行具体计算之外，通过前几项来猜想数列的通项公式也是不可或缺的能力. 为此，笔者以这个内容为准设计了一些变形问题. 问题1：如图8所示，请观察图中的图形排列以及其中所包含的点数，将空格当中的图形与点数填写完整，并写出点数的通项公式. 问题2：如图9所示，这些图形当中体现出了这样一系列规律：在图①当中，经过等边三角形的变化，形成了该多边形；在图②当中，经过正方形的变化，形成了该多边形；…，后面的图形也是以此类推. 那么，若正n边形所变化形成的多边形边数为an，则a6的值是多少？+++…+的值又是多少？问题3：观察图10所示的图形，按照其中的规律，当10条直线相交时，最多能够产生多少个交点？交点个数的通项公式是什么？一连串知识变形下来，学生对于数列通项公式的猜想思维感悟得更加深刻了. [（1）][（4）][（7）][（ ）][（ ）][（1）][（2）][（3）][（4）][（5）][2条直线相交，最多有1个交点][3条直线相交，最多有3个交点][4条直线相交，最多有6个交点][图8][圖9][图10] 不难发现，我们在高中数学教学当中所经常强调的“灵活思维”，实际上就是一种思考分析的习惯. 一旦这种习惯形成了，无论是面对灵活问题，还是灵活解答问题，都将不再是障碍. 于基础知识呈现阶段便勤于将知识进行变形，其所发挥出的思维铺垫作用，在接下来的深入学习当中体现得会十分明显. 在持续的变形推广过程当中，高中数学的灵活性特点得到了淋漓尽致的体现. 将基础知识作为变形推广的起点，能够把灵活性学习渗透到高中数学的每一个知识领域当中去，且可以让这个特点从知识接触之初便得以体现出来，使之能够伴随数学学习的全过程. 当变形推广基础知识的活动成为一种常态之后，便可以在学生的头脑当中树立起一种灵活多变的思维意识，于无形之中升华高中数学的学习效果.
随便看	微生物发酵制药企业的信息化管理路径探析 提升企业信息化管理实效性的策略分析 油田数字化的异构数据源整合与集成技术分析 中小企业市场营销存在的问题及对策分析 以打造优质基层水电企业为目标的动态人才开发管理 浅析建筑工程项目管理中的施工现场管理及优化对策 拓展训练在企业员工培训中的作用研究 体育经济视角下健身俱乐部的市场营销策略研究 电网企业“订单+定向”员工培养模式的创设 浅析建筑工程管理的影响因素与改进策略 浅谈项目经理在项目管理中应发挥的作用 浅谈国企培训师资体系建设 建立知识产权管理体系推动科技型企业创新发展 基于GJB5000A的软件控制研究 企业人力资源开发与绩效管理的应用研究 基于胜任力模型的人才招聘研究 船级社的法律地位及其责任制度研究 基于质量管理理论的知识型员工管理研究 业主在重大工程项目建设中面临的难题及对策分析 基于复杂网络理论的供应链管理研究综述及其展望 投资方案选择的层次分析模型 普惠金融视角下小贷公司发展策略分析 互联网背景下网络金融风险防范策略探讨 PPP模式下保障房建设的税务探讨 PPP模式下土地一级开发税收问题分析 hyperhilariously hyperhilariousness hyperhilariousnesses hyperhilarities hyperhilarity hyperhypocrisies hyperhypocrisy hyperidealistic hyperidealistically hyperimmunities hyper-immunity hyperimmunity hyperimmunization hyperimmunizations hyperimmunize hyperimmunized hyperimmunizes hyperimmunizing hyperinflated hyperinflation hyperingenuities hyperingenuity hyperinnervation hyperinnervations hyperinsulinaemia 广阔的沙地，大漠 广阔的沙漠 广阔的疆域 广阔的空间 广阔的郊野 广阔绵延的深草 广阔辽远的样子 广阔辽远，无边无际 广阔遥远 广陌 广陵 广陵客 广陵弦 广陵故事 广陵散 广陵散绝 广陵涛 广陵清曲 广陵绝响 广陵观涛 广陵集 广雅 广雅义疏 广雅疏证 广雅疏证拾遗

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。