《Matlab在IIR数字滤波器教学中的应用》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

Matlab在IIR数字滤波器教学中的应用

范文

程俊周慧

摘要：IIR数字滤波器的设计是数字信号处理的重要内容，Maflab具有强大的信号处理功能。本文利用Matlab仿真了IIR数字滤波器设计中抽样间隔的选择和频谱混叠问题的实例，通过分析频谱图形和衰减数据来帮助学生更好地理解IIR数字滤波器设计过程中的关键问题，从而达到事半功倍的教学效果。

关键词：IIR数字滤波器;脉冲响应不变法;频谱混叠

中图分类号：TP311.5 文献标识码：A

文章编号：1009-3044（2019）32-0243-02

本文以脉冲响应不变法设计im数字低通滤波器为教学实例，探讨了Matlab在数字信号处理教学中的仿真应用。脉冲响应不变法具有频率变换关系是线性的，数字滤波器的单位脉冲响应能完全模仿模拟滤波器单位冲激响应的波形，时域特性逼近性好的优点，适合设计低通、带通滤波器。但是这种方法中如何根据给出指标的不同选择抽样间隔T，以及如何解决频谱混叠现象是该内容的难点，课堂上通过Matlab仿真运用频谱图形和衰减数据结果来讲解，便于学生更好地理解IIR数字滤波器设计过程中的关键问题。

1抽样间隔T的选择问题

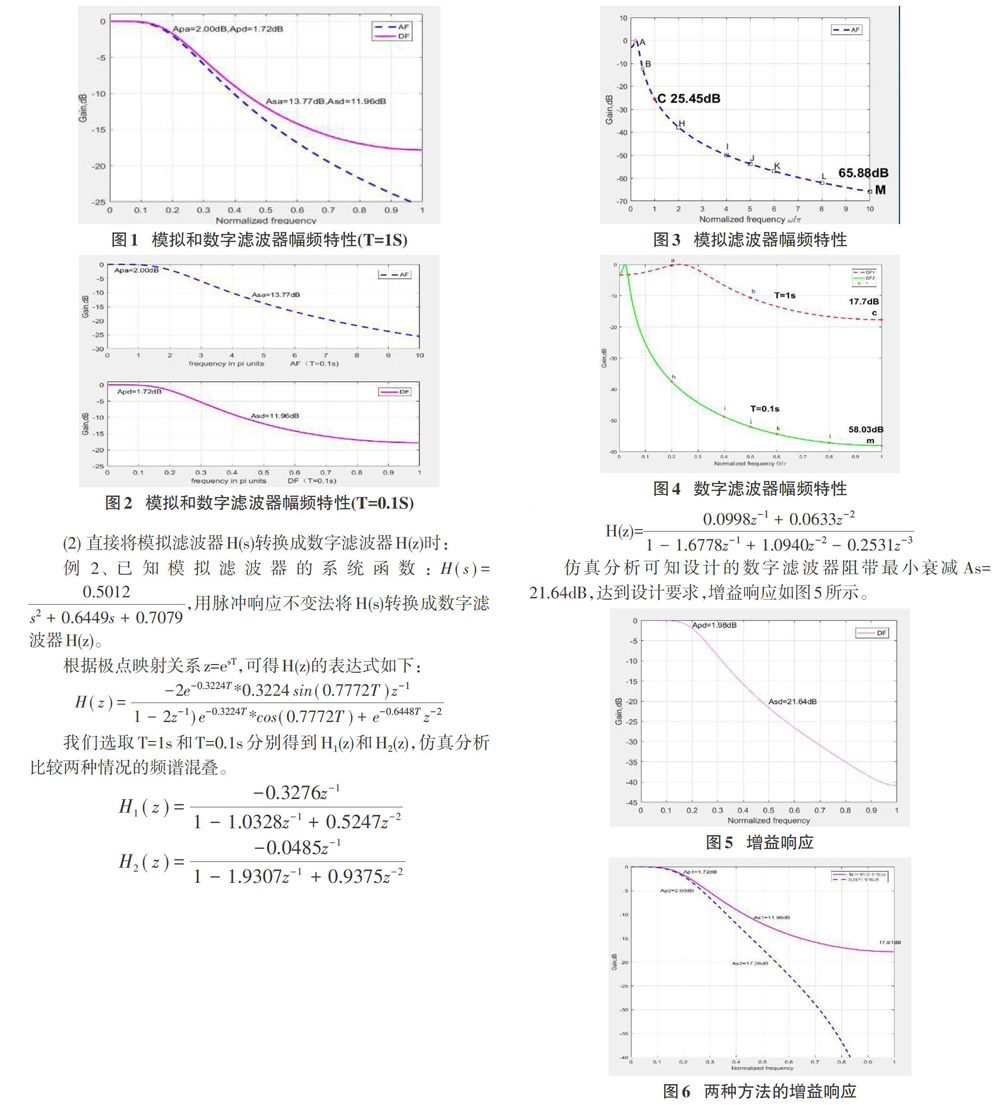
我们仿真研究T=ls和T=0.1s两种情况，根据以上n（s）和H（z）表达式，T不同时，模拟滤波器表达式不一样，而数字滤波器系统函数的表达式与T没有关系。这时设计的模拟滤波器和数字滤波器幅频特性如图1（T=ls）和图2（T=0.1 s）所示，虚线代表模拟滤波器，实线代表数字滤波器。比较发现模拟滤波器差别比较大，而数字滤波器的幅频特性相同。这说明当给定数字滤波器技术指标时，抽样间隔T的取值对频谱混叠程度的影响没有关系。所以为了计算简便，一般取T=1s。以T=1s为例，通带技术指标满足要求，但是阻带截止频率Ωs=0.5π时，模擬滤波器阻带衰减Asa=13.77dB，满足技术指标;而数字滤波器阻带衰减Asd=11.96dB，不满足设计指标，这是因为设计的模拟滤波器不是带限的，脉冲响应不变法设计的数字滤波器存在频谱混叠，使得数字滤波器在折叠频率π附近的衰减明显小于模拟滤波器对应频率点的衰减。

图3是模拟滤波器Hfs）的幅频特性，图4是T取不同值时数字滤波器的幅频特性，两幅仿真图的横坐标都是对π归一化的频率，横坐标服从线性关系，既数字角频率等于模拟角频率乘以T。

图3显示模拟滤波器通带很窄，阻带衰减慢。图4中，T=IS时，图3中的ABE点对应图4中的abc点，模拟滤波器的C点频率为3.14rad/s，衰减为25.45dB，而对应的数字滤波器c点衰减幅度却只有17.7dB，可见c点附近出现了严重的频谱混叠现象。T=0.1S时，图3中的H、I、J、K、L、M点对应图4中的h、i、j、k、l、m点，可以看出幅度特性很相似，只是在m点折叠频率盯（模拟频率为10π）时有很轻的混叠现象，模拟滤波器的M点频率为31.4rad/s，衰减为65.88dB，而对应的数字滤波器m点衰减为58.03dB。这个例子可知：给定了模拟滤波器的系统函数，转换成数字滤波器时，可以通过减小抽样间隔T，也就是增大抽样频率，减轻混叠现象。

2混叠问题的解决方案

前面分析可知：当滤波器的指标用数字域频率给定时，利用脉冲响应不变法设计数字滤波器，不能通过减小T来减少频谱混叠，那么如何有效地改善频谱混叠现象呢？

①增大阻带衰减。有效的方法是增加待设计的数字滤波器的阻带最小衰减As。例l中其他技术指标不变，如果增加As为：As>14dB，则根据指标计算可得N=3，数字滤波器系统函数如下：

②采用双线性变换法。双线性变换法的基本思想是采用非线性频率压缩方法，先将整个模拟频率轴压缩到±π/T之间，再用z=eST转换到z平面上。是一种能克服脉冲响应不变法频谱混叠的方法。例1的设计指标用两种方法实现，增益响应如图6所示，实线是脉冲响应不变法，虚线代表双线性变换法。阻带衰减分别是Asl=11.96dB（不满足指标），As2=17.28dB（满足指标），折叠频率π时，脉冲响应不变法的衰减是17.81dB（严重的频谱混叠），双线性变换法的幅度降为0，完全没有频谱混叠。数字滤波器的设计是数字信号处理的重要内容，在教学过程中运用Matlab设计具体的仿真实例，使学生对数字滤波器的设计过程、优缺点分析以及关键问题的解决有了更深入的理解。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。