《化归方法及在中学数学教学中的应用》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

化归方法及在中学数学教学中的应用

范文

高超

【摘要】中学数学离不开化归思想.在数学的解题方法中，化归思想对于提高解题效率、提高学生分析问题和解决问题的能力具有重要的作用.本文将结合数学教法，通过案例分析化归思想在教学中的应用，讨论在教学中如何加强化归思想方法的渗透以及在渗透化归方法时应注意哪些问题等，并提出加强化归思想的教学对策，从而培养学生的化归意识和学习能力.

【关键词】化归方法;中学数学;教学;应用

一、化归思想在数学新知识学习中的应用

化归思想在数学新知识学习中的应用很广，我们对新概念的学习往往是建立在旧知识的基础上的.例如，我们对代数的学习是从研究简单的数、式开始的，对于复杂的数、式，也是通过变换，将其归结为简单的数、式，进而解决问题的.在解一元一次方程组和一元二次方程时，仍离不开解一元一次方程，其解决问题的方法就是将问题转化为一元一次方程，然后解一元一次方程，从而得到问题的解.新知识与旧知识之间的联系，关键的一步就是转化.在数学中有一种重要的证明方法：数学归纳法，它也离不开化归法.

二、化归思想在教学中的渗透

数学教材体系的灵魂是数学思想，数学思想能够将数学概念、数学命题以及数学问题解决结合在一起，从而形成一个比较完善的体系.在高中数学教材中，化归思想方法出现的频率也比较高，并且渗透到了各个环节中.有些教师教学的时候非常重视做题量，自己做题比较多，也要求学生做大量的题目，为了做题而做题，对于学生解题能力的培养不够重视.做题不是没必要，深厚的解题功底是掌握数学知识的基础，但是我们不能只停留在这个初级阶段，还要理解这些操作背后的思想方法.一般情况下，数学问题的解答往往是通过已知条件来转化问题，从而达到解决问题的目的.教师在引导学生利用化归思想解答问题的时候，需要先对题目解答的过程和步骤进行分析，找到每一步的主要内容和作用，将其组织成为一个整体，然后对学生进行引导，帮助学生找到解答问题的办法和实质，在这种情况下，化归思想的作用便会比较明显.教师以此为基础将化归方法讲解给学生，然后通过化归方法来解答题目，这样能够帮助学生更好地掌握这种方法.

学生在学习数学的时候，知识的深化是逐步进行的，这也导致知识发展的不同阶段所反映出的数学思想也各不相同，这也能够将数学思想方法所具有的层次性体现出来.在解答问题的时候，我们经常会遇到需要多次化归的情况，并且有时候化归的方向是不一样的.这便要求我们在应用化归方法的时候，必须重视不同阶段知识再现的情况，和学生一起研究在不同阶段中化归方法形成的整个过程，这样能够启发学生的思维，帮助学生更好地认识化归思想.化归思想方法本身便是在学生思维启发的过程中慢慢形成的.所以，教师在教学的时候，首先需要重视问题解决之后的反思，通过这个过程来进行化归方法的提炼.在这种情况下，学生很容易了解、接受和掌握化归方法.并且在这个过程中，我们还需要认识到化归思想方法渗透需要较长的时间，其无法在短期内帮助学生提高能力.学生想要真正掌握化歸思想方法必须不断训练，循序渐进地进行.

三、化归思想在解题中的应用

化归思想在数学解题中的应用比比皆是.立体几何中相关的证明题、计算题，我们多将其转化到平面几何中来解决，或者将其转化到向量空间中去解决;多数三角函数的计算题或证明题，我们若直接解决会感到很吃力，若换个角度，运用数形结合的思想，将抽象的问题转化到直观的图形中，解决起来就容易多了;对复杂、非特殊的数列的求和问题，我们也是将其转化为较为简单、特殊的数列进行求和.多数数学问题的解决都离不开化归思想方法，只是所体现的形式不同罢了.总体来说，我们在解数学题时，计算题是利用规定的法则进行化归，证明题是利用公式、定理或已经证明了的命题化归，从而使问题得以解决.

（1）将未知的问题转化归结为已知的知识

把不知道的问题转化成为已经掌握的知识，并将二者结合在一起，然后通过较为熟悉的方法和知识进行新问题的解答，这种转化方式起到的效果比较好.比如，要求空间两条异面直线所成的角，在这种情况下，我们只需利用平行线进行转化，将其转化成为我们比较熟悉的两相交直线所成的角即可.

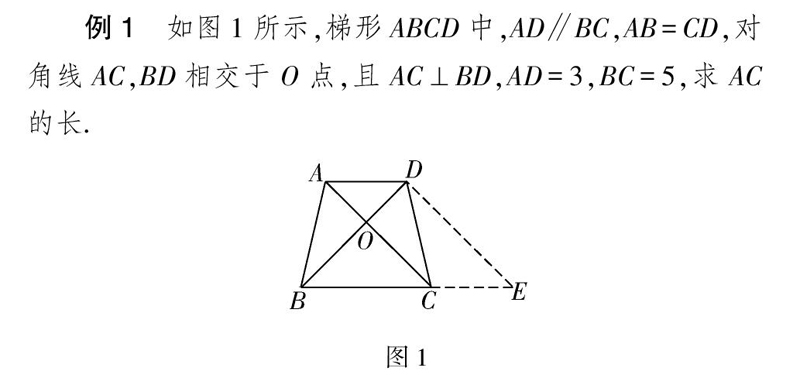
例1 如图1所示，梯形ABCD中，AD∥BC，AB=CD，对角线AC，BD相交于O点，且AC⊥BD，AD=3，BC=5，求AC的长.

图1

分析此题是根据梯形对角线互相垂直的特

点，通过平移对角线将等腰梯形转化为直角三角

形和平行四边形，使问题得以解决.

解过点D作DE∥AC交BC的延长线于点E，则得AD=CE，

AC=DE，所以BE=BC+CE=8.

∵AC⊥BD

∴BD⊥DE

又∵AB=CD

∴AC=BD

∴BD=DE

在Rt△BDE中，BD2+DE2=BE2

∴BD=42，即AC=42.

（2）将复杂问题转化归结为简单问题

在数学问题解答中，将较为复杂的问题简单化是非常普遍的一种方法.若一个问题很难直接解决，那么，我们可以对其进行深入的研究和观察，将其转变成为比较简单的问题，然后再进行求解.特别是将正向思维转变成为逆向思维很有意义，若教师经常对学生进行引导，让其注意问题的分析，并让其逆向思考问题，这样不但能够帮助学生更好地理解相关的逆向知识，还能让学生的思维更加灵活.

例2 已知x2+x-1=0，求x3+2x2+2009的值.

分析此题通过“化零散为整体”或利用降次来转化，可使问题得以解决.

解法一 ∵x2+x-1=0

∴x2=1-x

∴x3+2x2+2009=x（1-x）+2（1-x）+2009

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。