网站首页  词典首页

请输入您要查询的论文：

　

标题 基于特征融合稀疏表示的JPEG隐写分析
范文 刘慧兴　刘毅



摘 要： 提出一种新的JPEG图像隐写分析方法，即基于特征融合的稀疏表示隐写分析方法。首先介绍所选特征的提取方法并分析所选特征之间的互补性与冗余性，然后利用主成分分析方法将所选特征降维进行融合，最后在此特征上利用向量总变差进行稀疏求解，用稀疏表示进行隐写检测。理论分析和实验表明该方法比单一特征的稀疏表示具有更高的识别率。
关键字： 特征融合； 稀疏表示； PCA； 向量总变差
中图分类号： TN911.73?34 文献标识码： A 文章编号： 1004?373X（2015）07?0077?04
0 引 言
图像隐写分析是指对获取的图像进行统计分析以判断其是否含有隐藏信息的技术。JPEG图像作为一种最常见的图像，对其进行隐写检测研究十分必要，其通用隐写分析过程主要包括两部分：特征提取和分类器的设计。提取特征是否有效直接关系着后续的检测准确率，在现存的通用JPEG隐写分析中，检测准确率较高的特征有基于校准的特征[1]、偏序Markov特征[2]、基于Markov过程的特征[3]等。隐写检测分类器的设计包含很多种，如支持向量机、贝叶斯分类器等，2013年，Zhang等人提出一种基于稀疏表示的隐写检测方法[4]，首次将稀疏表示应用于图像隐写检测中，并证明了基于稀疏表示的隐写检测方法具有良好的抗噪性，但是文献[4]中的隐写检测特征是基于单一特征的且运用[l1]范数来进行稀疏求解，由于单一特征包含的综合分类信息有限，再加上隐写算法的不断改进和提高，因此在检测率和健壮性方面具有局限性。近年来，为了提高隐写检测准确率和隐写特征的通用性，研究者们提出采用一定的手段将多个原始特征结合来进行隐写检测的方法，Manga等称这类结合方法为特征融合[5]。本文在文献[4]的基础上提出一种基于特征融合稀疏表示的JPEG图像隐写分析方法，融合特征时需要考虑特征之间的互补性与相关性，简单的串行不但不会提高准确率而且还会引起“维数灾难”问题。本文选取基于校准的特征[6]和基于Markov过程提取的DCT块内和块间的特征[7]，利用 PCA 对两组特征进行变换，去除特征中的冗余信息，组成隐写检测特征，基于此融合特征选取稀疏表示来进行隐写分析，使用向量总变差进行稀疏求解。实验表明，本文提案的方法优于现存的单一特征稀疏表示的方法[4]，在保持健壮性的同时提高了JPEG隐写分析的准确率。
1 特征提取及特征间相关性与冗余性分析
1.1 基于校准特征的提取
Kodovsky等人在PEV[1]方法的基础上将隐写分析图像特征与校准图像特征串行融合[6]，得到548维特征。方法如下：
（1） 计算DCT系数亮度部分直方图矩阵[Hl，]其中[l∈{-5，…，5}]；
（2）计算单个DCT块内直方图矩阵[Hi，j，]其中[（i，j）∈{（1，2），（2，1），（3，1），（2，2），（1，3）}]；
（3） 计算双直方图矩阵[Gdi，j，]其中[{i，j=1，…，8，d=]
[-5，…，5}]；
（4） 对于所有的DCT块，计算总的方差[V；]
（5） 解压JPGE图像，计算块内分块特性[Ba，][a=1，2；]
（6） 计算相邻DCT块系数的共生矩阵[Cs，t，][（s，t）∈]
[[-2，+2]×[-2，+2]]；
（7） 计算Markov概率转移特征，求一阶概率转移矩阵在水平、垂直、主对角和副对角4个方向上的均值，记为[Mm，n]；
（8） 组合上述7种特征记为[Fr。]利用校准技术对隐写分析图像的最外层各裁剪4行4列，再次进行JPEG压缩，对校准图像重新提取、组合以上特征得到校准图像特征记为[Fc。]
（9） 将[{Fr?Fc}]特征称为[PEV?274，][{Fr，Fc}]特征称为[PEV?548。]
以上具体的计算公式参见文献[1]。
1.2 基于Markov块间和块内特征的提取
Chen等人对原来的Markov特征[3]扩展得到486维特征[7]，方法如下：
（1） 提取JPEG量化系数矩阵。
（2） 按水平、垂直、主对角和副对角4个方向对系数矩阵求差，计算相邻JPEG量化系数中满足差值为[{dci-dcj=d}]的组合概率，其中[{dci，dcj∈-T，…，T}，][T]为阈值。
（3） 分别对得到的4个差值矩阵计算其一阶转移概率矩阵（Transition Probability Matrix，TPM），其中水平方向公式如下：
[Mhn，m=Pr[Fhu，v+1=n|Fhu，v=m]=u，vδ[Fhu，v=m，Fhu，v+1=n]u，vδ[Fhu，v=m]] （1）
分别计算4个方向上的一阶转移概率矩阵，最后得到[4×（2T+1）2]维块内特征。
（4） 将位于各个DCT块中相同位置的DC系数提取，组成DCT系数矩阵，分别求水平和垂直方向的一阶转移概率矩阵，得到[2×（2T+1）2]维块间特征。
（5） 最后取阈值[T]为4得到486维块内和块间特征，称为Chen?MPB特征。
1.3 两组特征间的互补性和冗余性
从上述的提取特征过程，可以看到Chen?MPB块内特征主要关心的是修改DC系数后对块内局部引起的变化，然而有些隐写算法对局部的扰动并不明显，如[F5]隐写算法[8]对DC系数为0和1时则重新嵌入，其隐写过程中将产生新的值为0的DC系数，因而此时仅从局部特征进行分析不全面。PEV?548特征中系数直方图、方差、亮度等特征属于全局特征，它与局部特征相比具有统计量范围大的特点，但有些隐藏算法采取一些修补技术来控制全局特征的扰动，如扰动量化（Perturbed Quantization，PQ）[9]隐写算法会优先选择小数部分靠近0.5的DCT系数，公式如下：
[Au，v-Au，v∈[0.5-ε，0.5+ε]] （2）
PQ隐写方法会尽量减小全局变化，但该方法无法保持和修复局部DCT系数变化。
另外，Chen?MPB特征是基于一阶Markov过程提取的，而PEV?548特征是基于校准技术的，因此它们具有不同的特征分布模型，不同的模型下隐写算法对特征具有不同的改变程度，很难做到既要兼顾不同的分布模型，又使得每个模型下的扰动量达到最小[10]。
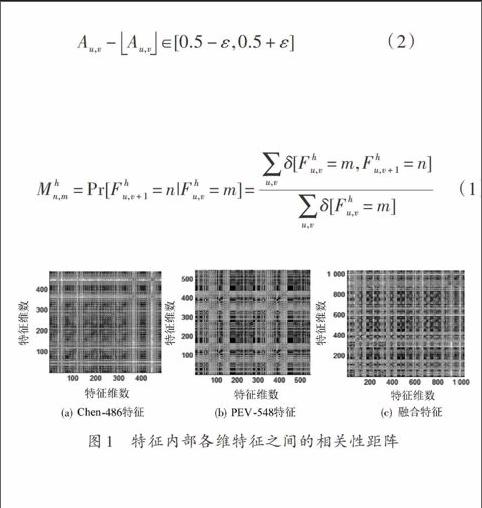
从上述中可以知道这两种特征具有一定的互补性。但这两组特征之间也存在一定的冗余性，这主要是因为各个特征在提取时有类似之处，例如：PEV?548特征中的Markov特征就包含了Chen?MPB特征中DCT块内一阶TPM的计算，即它取各个方向的一阶TPM的均值并校准作为特征；另一方面，各类特征内部中各维特征之间也存在着相关性，图1为特征内部之间各维之间的相关性矩阵。
图1 特征内部各维特征之间的相关性距阵
图1中黑点代表各维特征之间具有相关性。从图1中可以看出（a）、（b）、（c）这三组特征除了对角线外各维特征之间还存在着较大的相关性。因此，在融合特征时需要采用一定的方法去除冗余特征，主成分分析（Principal Component Analysis，PCA）是一种有效的线性变化方法，它可以有效消除变量之间的线性相关性，从而去除冗余信息[10]，本文选用PCA方法来进行特征的融合。
2 稀疏表示
稀疏表示是指在一个合适的基或者字典上，用只含有少量非零元素的稀疏来描述原始的信号，它简化了信息处理的求解过程，同时通过这些少量的非零值，还可以用非线性的最优化方法来重构原始信号。稀疏表示可以追溯到20世纪90年代，1993年S.Mallat等人第一次介绍匹配追踪算法（Matching Pursuit，MP）[11]，从那时起，超完备稀疏表示成为信号处理领域的热点。
图2描述了稀疏表示模型，其中[D=[d1，d2，…，dn]，][D∈Rm×n]为一个超完备字典，其包含[n]单原子。对于任意信号[y∈Rm×1]可以由这些单原子来线性表示，向量[x∈Rn×1]为信号[y]的稀疏表示系数。
图2 稀疏表示模型
对于每个信号[y]，由式（3）可以得到稀疏[x0]的线性重构系数。
[x0=argminx0 s.t Dx=y] （3）
然而，式（3）是一个NP问题，想要解决它非常难。所以，为了确保稀疏，式（3）可以转换为式（4）：
[x1=argminx1 s.t Dx-y2≤ε] （4）
这是一个[l1]范数问题，从而可以利用基追踪法[12]来求解。数学上对范数定义如下：若[x=（x1，x2，…，xn）T，]则[p]范数定义为：
[xp=（x1p，x2p，…，xnp）1p] （5）
因此[l1]范数可以写成如下形式：
[x=x1+x2+...+xn] （6）
由式（6）可知，[l1]范数等价于求解一个向量的长度，因此有可能造成两个向量差异比较大，同时它们的[l1]范数却非常接近，这样就会造成错误的结果，如图3所示。本文选用向量总变差模型（Total Variation，[TV]）来代替[l1]范数进行稀疏表示，向量总变差模型最早由Rudin等人引入[13]，其对细节的描述能力很强，形式如下：
[TV（x）=ijDijx2=ij（Dh，ijx）2+（Dv，ijx）2] （7）
其中[Dh，ijx]和[Dv，ijx]分别为水平和垂直方向的偏导数。从式（7）可以看出二维处理模式比[l1]范数求解更加复杂，从统计的角度来看，直接对一维信号向量进行总变差运算同样能达到较好的效果，其变化形式如下：
[TVvec（x）=i=2Nxi-xi-1] （8）
从式（8）可以看出变形的向量总变差运算复杂度与[l1]范数求解同级，于是将求解最小[l1]范数问题转化为下式：
[minTVvec（x）+y-Ax22 subject to Ax=y] （9）
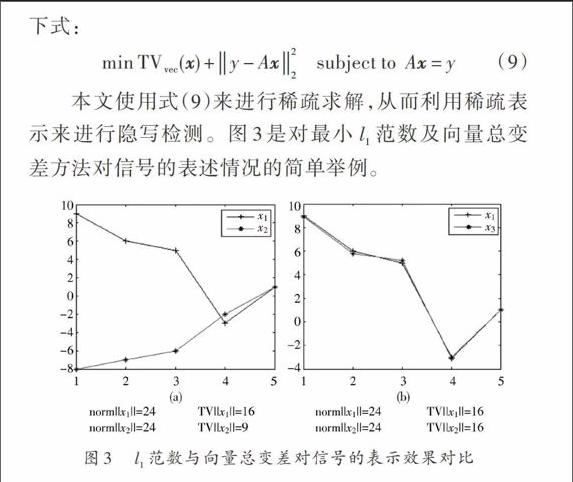
本文使用式（9）来进行稀疏求解，从而利用稀疏表示来进行隐写检测。图3是对最小[l1]范数及向量总变差方法对信号的表述情况的简单举例。

图3 [l1]范数与向量总变差对信号的表示效果对比
图3（a）中[x1]与[x2]的[l1]范数相同但是两个向量的反差很大（可以从向量总变差上来反映），这说明[l1]范数的求解误差是存在的。图3（b）中两个相似的信号[l1]范数相同，向量总变差也相同，这说明向量总变差对信号的测量比[l1]范数有更好的效果。
3 本文提案的隐写检测方法
本文所选的隐写检测特征是由Chen?MPB特征和PEV?548特征组成的，由于这两组特征之间具有互补性，因而组合这两组特征将会包含更加丰富的分类信息，理论上融合的特征隐写检测准确率比单一特征隐写检测的准确率要高；另外在第1节中还提到这两组特征间具有冗余性，本文采用PCA来消除两组特征之间的冗余性，从而形成融合的特征，即本文方法的特征。分类器选用基于向量总变差模型的稀疏表示来进行分类。具体的隐写检测步骤如下：
（1） 特征提取：对训练集图像和测试集图像分别用Kodovsky、Chen等人中的方法提取特征[6?7]，得到PEV?548和Chen?MPB等特征集；
（2） 特征融合以及超完备字典生成：将提取的PEV?548特征与Chen?MPB特征组合成特征集[F=][{f1，f2，…，fr}，][r]为组合特征维数，[S={S1，S2，…，Sn}，][n]为训练集样本数，[S]为训练集合，将特征进行归一化处理，并保存各维特征的均值[u，]标准差[s，]后续检测时需要对测试样本进行归一化处理，利用PCA选择特征中累积方差比例达到总方差99%以上的[m]维，保存PCA过程中的变换矩阵c?matrix，以及PCA处理过的训练样本集[S，]其中[S]为稀疏表示中的超完备字典。

（3） 稀疏求解：对于测试集[Y]与超完备字典[S，]利用步骤2中生成的均值[u]、标准差[s]对测试集[Y]进行归一化处理，对于每个测试样本[y]，利用公式（8）求出[y]的稀疏表示[x]。
（4） 计算残差：[x][∈Rn×1]其中每一维对应着超完备字典[S]中的一个向量，分别提出每一类[Yi]所对应的[x∈][Rk×1，]其余[n-k]维设置为0，由超完备字典[S]分别重构出[yi=Sxi，]分别计算[Dyi=yi-y，]即重构[yi]与检测图像[y]之间的残差。
（5）确定[y]的类别：利用决策函数：[identify（y）=][argminDyi]决定[y]是否是隐写图像。
4 实验及结果分析
4.1 实验参数和条件
本文选取的图像源为BOWS图像库（在10 000幅中随机选取4 500幅）。为排除压缩时质量因子对隐写检测的影响，将4 500幅图像全部压缩成质量因子为85的JPEG图像。随机选取其中的3 000幅图像，分别利用Jstep[14]、nsf5（基于F5上的改进）[15]和PQ[9]等隐写工具在嵌入率为0.25 bpc（bit per coefficient，bpc即每嵌入1比特信息需要修改0.25个DCT系数），0.50 bpc，0.75 bpc的情况下分别得到3 000幅JPEG隐写图像，称为阳性集；剩余的1 500幅JPEG图像为未嵌入隐藏信息的图像，称为阴性集。
4.2 基于融合特征与单一特征的隐写检测准确率的比较
在基于nsf5隐写方法嵌入率为0.25 bpc情况下，分别对单一PEV?548特征、 单一Chen?MPB特征、PCA融合特征在不同的维数下进行测试，统计融合特征与单一特征在不同的维数下隐写检测的准确率。JPEG图像1 500对，其中隐写图像1 500幅，原始图像1 500幅。交叉测试，每次训练集为1 000对，测试集为500对，结果为两次实验的平均值。图4为融合特征与单一特征在不同维度下隐写检测的准确率。

图4 融合特征与单一特征隐写
检测准确率的对比
从图4可以看出基于PCA融合后的特征，在一定的维度下其隐写检测准确率趋于平稳，且比单一特征的隐写检测准确率要高，这说明两组特征之间具有一定的互补性；另外经过PCA降维在300维、400维时其隐写检测准确率与无PCA处理（1 034维）的隐写检测准确率相比仅差0.1%左右，这表明两组特征之间有较强的冗余性。
4.3 本文方法与文献[4]隐写检测方法实验结果对比
表1为文献[4]中基于PEV?274特征[l1]稀疏表示隐写检测方法（简称[l1]方法）和本文提案的隐写检测方法的准确率比较，其中经PCA处理的融合特征的维数为350维。
表1 本文方法与[l1]方法隐写检测正确率比较 %
[隐藏信息
嵌入率 /bpc＼&Jstep＼&nsf5＼&PQ＼&[l1]方法＼&本文方法＼&[l1]方法＼&本文方法＼&[l1]方法＼&本文方法＼&0.25＼&88.80＼&93.60＼&86.53＼&90.20＼&90.33＼&91.27＼&0.5＼&89.60＼&94.47＼&91.87＼&93.40＼&92.07＼&93.40＼&0.75＼&91.47＼&95.53＼&92.40＼&96.53＼&94.47＼&95.13＼&1.0＼&93.53＼&97.07＼&95.33＼&97.00＼&97.13＼&97.60＼&]
5 结 语
本文将特征融合与稀疏表示结合来进行JPEG图像的隐写检测，选取2组具有一定互补性的JPEG通用隐写分析特征，并利用PCA去除特征的冗余成分得到融合特征，实验表明在不同维度下基于PCA融合的特征比单一的PEV?548特征的隐写检测准确率提高约2%。另外，基于融合特征利用向量总变差模型进行稀疏表示的方法对nsf5等强隐写方法，相比采用单一校准特征、利用[l1]范数稀疏表示方法[4]，在准确率上能提高约2%；对于Jstep经典隐写算法，本文提案的方法在隐写检测准确率上提高了约4%。
参考文献
[1] PEVNY T， FRIDRICH J. Merging Markov and DCT features for multi?class JPEG steganalysis [C]// SPIE Proceedings of Electronic Imaging， Security， Steganography， and Watermarking of Multimedia Contents IX. San Jose， CA： SPIE， 2007， 6505： 301?314.
[2] DAVIDSON J， JALAN J. Steganalysis using partially ordered Markov model [C]// Proc. of the 12th Internationa1 Workshop on Information Hiding. Bohme R， Berlin： Springer?Verlag， 2010： 143?157.
[3] S HI Y Q， CHEN C， CHEN W. A Markov process based approach to effective attacking JPEG steganography [C]// Information Hiding. [S.l.]： Springer Berlin Heidelberg， 2007： 249?264.

[4] ZHUANG Zhang， DONG hui?hu， YANG Yang，et al. Computational intelligence and security （CIS） [C]// 2013 9th International Conference on DOI. [S.l.]： [s.n.]， 2013： 437?441.
[5] MANGAI U G， SAMANTA S， DAS S， et al. A survey of decision fusion and feature fusion strategies for pattern classification [J]. IETE Technical review， 2010， 27（4）： 293?307.
[6] KODOVSKY J， FRIDRICH J. Calibration revisited [C]// Proceedings of the 11th ACM Workshop on Multimedia and Security. New York： ACM Press， 2009： 63?73.
[7] Chen C， Shi Y Q. JPEG image steganalysis utilizing both intrablock and interblock correlations [C]// IEEE International Symposium on Circuits and Systems. [S.l.]： IEEE， 2008： 3029?3032.
[8] WESTFELD A. High capacity despite better steganalysis （F5?a steganographic algorithm） [C]// 4th International Workshop， volume of Lecture Notes in Computer Science. New York： Springer?Verlag， 2001， 2137： 289?302.
[9] FRIDRICH J， GOLJAN M， SOUKAL D. Perturbed quantization steganography [J]. ACM Multimedia Systems， 2005， 11（2）： 98?107.
[10] 黄炜，赵险峰，冯登国，等.基于主成分分析进行特征融合的JPEG隐写分析[J].软件学报，2012（7）：1869?1879.
[11] MALLAT S， ZHANG Z. Matching pursuit with time?frequency dictionaries. IEEE Transactions on Signal Processing， 1993， 41： 3397?3415.
[12] TROPP J A. Greed is good： Algorithmic results for sparse approximation [J]. IEEE Transactions on Information Theory， 2004， 50（10）： 2231?2242.
[13] LI Ru?din， OSHR S， FATEMI E. Nonlinear total variation noise removal algorithm [J]. Physea D， 1992， 60： 259?268.
[14] HSU C T， WU J L. Hidden digital watermarks in images [J]. IEEE Transactions on Image Processing 1999， 8（1）： 58?68.
[15] FRIDRICH J， PEVNY T， KODOVSKY J. Statistically undetectable JPEG steganography： Dead， ends， challenges， and opportunities [C]// Proceedings of the 9th ACM Multimedia & Security Workshop. Dallas， TX： ACM， 2007： 3?14.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 3:37:48