网站首页  词典首页

请输入您要查询的论文：

　

标题 新的代理数字签名方案
范文

摘 要： 谷利泽等人提出一个新型代理数字签名方案，鲁荣波等人对其进行了分析与改进，杨丽等人证明了改进方案不满足公钥替换攻击，给出了攻击方法，并在此基础上提出一种改进的代理签名方案。分析杨丽等人提出的新方案，指出该方案增加了计算复杂度，并提出两种改进的代理数字签名方案。实验结果表明改进的方案具有较强的安全性也能够防止公钥替换工具，并减少了计算复杂度，提高了效率。
关键词： 数字签名； 代理签名； 公钥替换攻击； 计算复杂度
中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）08?0043?04
A new scheme of proxy digital signature
LIAO Xiao?ping， HOU Xiang， WEI Hong?chun
（Department of Computer Science， Sichuan University of Arts and Science， Dazhou 635000， China）
Abstract： Professor Gu Li?ze， et al made a new scheme of proxy digital signature， which was analyzed and improved by Lu Rong?bo， et al. However， Yang Li， et al proved that the improved scheme can not satisfy the public key substitution attack， pointed out the attacking method， and made a new improved proxy signature scheme based on the previous schemes. In this paper， the new scheme proposed by Yang Li， et al is analyzed， the calculation complexity of theirs is pointed out， and two improved proxy signature schemes are proposed based on the analysis of the previous schemes. The new schemes have strong security， can prevent any public key replacement tool， reduce complexity and increase efficiency.
Keywords： digital signature； proxy signature； public key substitution attack； computational complexity
0 引 言
代理签名是由Mambo等人在1996年提出来的[1]，指的是原始签名人将自己的签名权委托给代理签名人行使其签名权力，在最近几年，以代理签名为基础，相继提出了许多新的代理签名方案[2?5]。代理签名技术的应用非常广泛，但在一些特殊情况下要求能够隐藏代理签名人的身份，验证者无法从代理签名中识别出代理签名人的身份，只有在需要的情况下，验证者可以通过原始签名人来揭示代理签名人的身份，既要求代理签名方案具有匿名性。基于此，2002年Shum和Weil提出了一个匿名代理签名方案[6]，但它不具备安全性，无法抵抗原始签名人的恶意攻击[7]。此后，谷利泽等人提出了一种新型的代理签名方案[8]，指出此方案满足可验证性、不可伪造性、匿名性、可追踪性、不可否认性和防止代理权滥用六条性质，鲁荣波等人证明了它无法抵抗原始签名人伪造攻击[9]，并给出了一个改进的方案（以下简称LHWM方案），杨丽等人证明了鲁荣波等人提出的方案无法抵抗原始签名人替换公钥攻击，并对方案进行改进，提出了一个改进的方案（以下简称YZ方案）[10]。本文指出杨丽等人方案在保证安全的前提下增加了计算复杂度，并提出了两个改进的匿名代理数字签名方案。这两个改进方案克服了杨丽等人方案的缺陷，具有高安全性的同时在效率方面也具有优势，从而具有更好的实用性。
1 LHWM方案的密码分析
LHWM方案回顾：方案的参加者包括：原始签名者、代理签名者、签名验证者。
1.1 系统参数初始化
[p]和[q]是任意的两个大素数并且满足条件[qp-1]，[g∈Z*q]并且满足[gq=1modp（g≠1）；h（?）]为安全的哈希函数；[A]是授权书，用来定义原始签名者[A]对代理签名者[B]代理权限的约定，[A]为原始签名者，[B]为代理签名者；[V]为验证者；[A]的私钥为[xA]，公钥为[yA=gxAmodp]并将[yA]公开； [B]的私钥为[xB]，公钥为[yB=gxBmodp]并将[yB]公开；[IDB]为[A]和[B]共同生成的代理私钥，[yp=gxpmodp]为对应的代理公钥；代理签名者[B]的标识为[IDB]；签名者的标识为[IDP]；需要签名的消息为[m]，[σ=Sig（m，x）]是签名者用私钥x对消息[m]的一个离散对数型数字签名；[Ver（y，σ，m）]与签名算法相对应的验证算法；[y]为签名者的公钥；返回值为真或为假。
1.2 代理密钥对生成算法
（1） 原始签名者通过安全信道发送[mw]给[B]。[B]如果认为授权是合法的，则计算生成自己的代理私钥[sB，r1]和[s1]。过程如下：[?kB∈RZ*q]，[rB=gkBmodp]，[sB=][xB+kBrBmodq ?k1∈RZ*q，][r1=gk1modp，][s1=] [xBh（rB，IDB，r1）+][k1modq]。然后[B]把生成的密钥值及身份标识[（rB，IDB，r1，s1）]通过安全信道发送给[A]。[A]验证等式[gs1=yh（rB，IDB，r1）Br1modp]是否成立，若成立，则A秘密保存[（rB，yB，IDB）]，以备用来揭示代理者的身份，最后[A]计算[YP=yBrrBBmodp]，并将其写入[mw]中。
（2） 原始签名者[A]计算[rA]和[sA]，计算如下：[?kA∈RZ*q，rA=gkAmodp，][sA=xAh（mw，rA）+kArAmodq。] 然后[A]把[（rA，sA，mw）]通过安全信道发送给[B]，[B]验证等式[gsA=yh（mw，rA）ArArAmodp]是否成立，若成立，[B]秘密保存[（rA，sA，mw，sB）]。
（3） [B]生成代理私钥[xP]，即[xp=sA+sB]。
1.3 代理签名算法
代理签名人[B]首先验证消息[m]是否符合授权证书[mw]的约定，若[m]满足要求，则[B]利用代理私钥[xp]产生代理签名[σP=Sig（m，xp）]，得到代理签名值[（m，σp，mw，rA，yA）]。
1.4 代理签名验证算法
（1） 验证者[V]得到代理签名值[（m，σp，mw，rA，yA）]，首先验证消息[m]是否符合[mw]的约定，若[m]满足要求则进入下一步，否则认为代理签名[σP]无效。
（2） 验证者[V]利用代理签名[（m，σp，mw，rA，yA）]计算：
[yp=yh（mw，rA）ArArAYpmodp]
式中：[Yp]是从[mw]中取得，然后检验等式[Ver（yp，σp，m）=true]是否成立，若成立，则认为代理签名有效，否则无效。
1.5 揭示代理者身份算法
（1） 验证者[V]向原始签名者[A]提供代理签名[（m，σp，mw，rA，yA）]，[A]使用代理签名验证算法验证代理签名的有效性，如果有效，则进入下一步。
（2） 原始签名者[A]从[mw]中取出[Yp]，然后依次取出在代理密钥对生成阶段保存的[（rB，yB，IDB）]，判断等式[Yp=yBrrBBmodp]是否成立，如果存在[（rB，yB，IDB）]满足这个等式，则[IDp]是实现代理签名[（m，σp，mw，rA，yA）]的代理签名者。
2 对YZ改进方案分析
YZ对LHWM方案的攻击方案以及YZ改进方案请见文献[10]，此处只对YZ改进方案的性能进行分析。
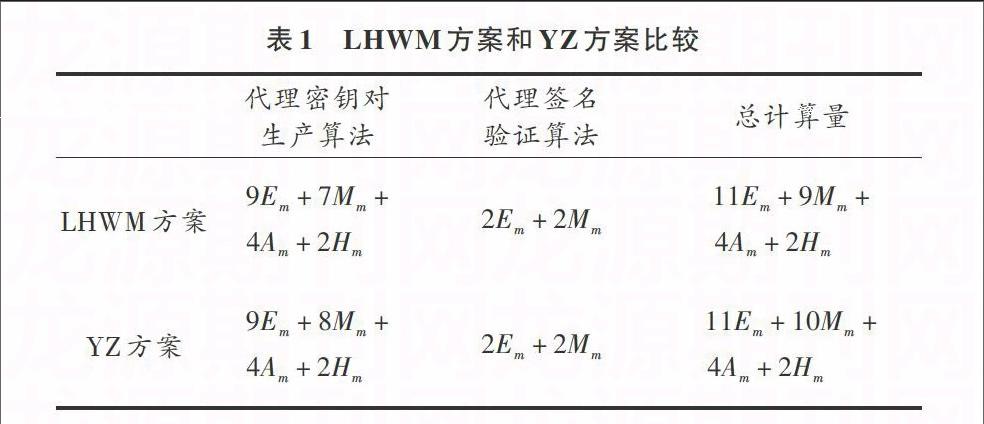
表1列出了LHWM方案和YZ方案代理密钥对生成算法和代理签名验证算法所需计算量的对比，其中两个方案的代理签名算法与揭示代理者身份算法的计算量相同，在此不再详述。令[Am]表示群加法运算的计算量、[Mm]表示群乘法运算的计算量、[Em]表示群指数运算的计算量和[Hm]表示哈希函数运算的计算量。
表1 LHWM方案和YZ方案比较从表中可以看出，YZ方案比LHWM方案多了一个群乘法运算。所以改进后的方案增加了计算的复杂度。
3 改进方案
3.1 改进方案1
3.1.1 系统参数初始化
同第1.1节系统参数初始化。
3.1.2 代理密钥对生成算法
（1） 原始签名者[A]随机选择数[kA∈Z*q]，计算[rA=gkAmodp]，[A]把[（mw，rA）]通过安全信道发送给[B]。[B]如果认为授权是合法的，则生成自己的代理私钥[sB，r1]和[s1]。过程如下：
[?kB∈RZ*q]，[rB=gkBmodp] ， [sB=xBmodq] ，
[?k1∈RZ*q]，[r1=gk1modp]，[s1=xBh（rB，IDB，r1）+k1modq]
然后[B]把生成的密钥值及身份标识[（rB，IDB，r1，s1）]通过安全信道发送给[A]。[A]验证等式[gs1=yh（rB，IDB，r1）Br1modp]是否成立，若成立，则[A]秘密保存[（rB，yB，IDB）]，以备用来揭示代理者的身份，最后[A]计算[Yp=yBrrBBmodp]，并将其写入[mw]中。
（2） 原始签名者[A]利用步骤（1）中得到的[kA]和[rA]，计算：[sA=xAyAh（mw，rA）+kArAmodq]，然后[A]把[（rA，sA，mw）]通过安全信道发送给[B]，[B]验证等式[gsA=yyAh（mw，rA）ArArAmodp]是否成立，若成立，[B]秘密保存[（rA，sA，mw，sB）]。
（3） [B]生成代理私钥[xp]，即[xp=sA+sB]。
3.1.3 代理签名算法
同第1.3节代理签名算法。
3.1.4 代理签名验证算法
（1） 同第1.4节（1）。
（2） 验证者[V]利用代理签名[（m，σp，mw，rA，yA）]计算：[yp=yyAh（mw，rA）ArArAyBmodp]其中[yp]是从[mw]中取得，然后检验等式[Ver（yp，σp，m）=true]是否成立，若成立，则认为代理签名有效，否则无效。
3.1.5 揭示代理者身份算法
同第1.5节揭示代理者身份算法。
3.2 改进方案2
方案2只对方案1作如下几处修改，其他步骤同方案1，具体如下：
方案1的代理密钥对的生产阶段（1）中的等式[sB]改为：[sB=xBrAmodq]，代理签名验证算法中的验证等式改为：[yp=yyAh（mw，rA）ArArAyBrAmodp]。
3.3 改进方案分析
方案1和方案2具有相似性，所以以方案1为例分析改进方案的安全性。
3.3.1 可验证性
定理1 代理签名者[B]使用代理私钥[xp]，代表原始签名者[A]对消息[m]签名，验证者[V]利用代理签名[（m，σp，mw，rA，yA）]计算代理公钥： [yp=yyAh（mw，rA）ArArAyBmodp]然后使用[yp]验证相应的代理签名，那么：
[yp=gxpmodp]
[gxp=gsA+sBmodp=gxAyAh（mw，rA）+kArA+xBmodp =gxAyAh（mw，rA）×gkArA×gxBmodp =（gxA）yAh（mw，rA）×（gkA）rA×gxBmodp=yyAh（mw，rA）A×rrAA×gxBmodp =yyAh（mw，rA）A×rrAA×yBmodp=yPmodp]
即：[yp=gxpmodp]成立，证毕。
由于代理签名[（m，σp，mw，rA，yA）]包含[yA]，表明这是原始签名者[A]承认的代理签名。
3.3.2 不可伪造性
（1） 代理签名的不可伪造性
① 由于[yp=yyAh（mw，rA）ArrAAyBmodp]，所以根据[yp]，伪造者无法伪造[xp]。因为已知[yp]求[xp]是离散对数问题。
② 根据，[xp=sA+sBmodq]，如果伪造者想伪造代理签名者[B]的代理签名，伪造者必须同时具备以下两个条件：
第一个条件：伪造[sA]，因为[sA=][xAyAh（mw，rA）+][kArAmodq]，而[A]的私钥[xA]和[kA]对伪造者都是无法得到的，所以伪造者不可能伪造[sA]。
第二个条件：伪造[sB]，由于[sB=xBrAmodq]，而[xB]是[B]的私钥，所以伪造者不可能伪造[sB]。所以，根据[xp=sA+sBmodq]，伪造者不可能得到[xP]。
③ 原始签名者[A]也不可能伪造代理签名者[B]的代理签名，因为[A]是不可能得到[xP]的。
（2） 公钥的不可伪造性
如果原始签名人[A]随机选择数[rA′，xp′∈Z]，构造等式：[yp′=y′yA′h（mw′，rA′）ArA′rA′yB′rA′modp=gxp′modp]若要求得[yA′]要比求解有限域上离散对数问题还要困难。所以该方案能抵抗公钥替换攻击。总之，除了代理签名者[B]，任何人都无法伪造代理签名。
3.3.3 防止代理权滥用
（1） 代理权无法转移，[（rA，sA，mw）]是不可更改的，且[Yp]包含在[mw]中，一旦原始签名者[A]指定代理签名者[B]，[yp]就已经确定，除非[B]把[xp]给他的代理者，否则[B]不能利用[（rA，sA，mw）]再次代理授权。
（2） 代理签名者无法越权：代理签名验证算法的第1步就是验证消息[m]是否符合代理授权书[mw]的约定，如果不符合，那么签名无效，所以[A]可以充分利用代理授权书[mw]有效约束[B]代理权限范围。
3.3.4 匿名性和身份确认
验证者[V]利用代理签名[（m，σp，mw，rA，yA）]计算代理公钥：[yp=yyAh（mw，rA）ArrAAyBmodp]验证这个代理签名，[（m，σp，mw，rA，yA）]没有包含代理签名者身份，已知[Yp]是无法推出[yB]的，由此可见，验证者[V]能够验证代理签名的有效性，但并不知代理签名者的身份。
在必要时，在原始签名者[A]的帮助下，验证者[V]利用揭示代理者身份的算法，能够揭示代理签名者的身份。
3.3.5 不可否认性
（1） 从代理签名生成方式看，有效代理密钥生成包括了代理签名人[B]的身份信息，因此，他不能否认自己对消息[m]的代理签名。
（2） 从不可伪造性证明看，原始签名人及任何第三方不能伪造代理签名，所以代理签名者不能否认代理签名是由自己产生的。
3.3.6 性能分析
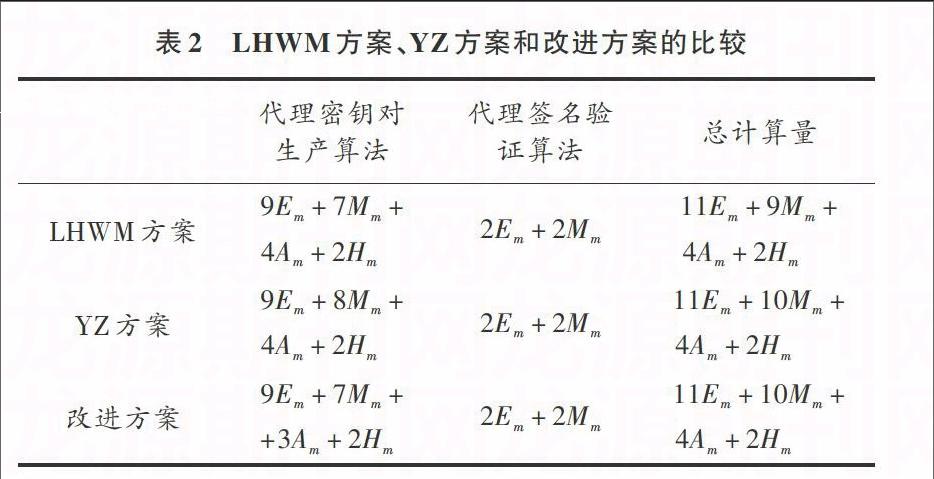
表2列出了LHWM方案、YZ方案和改进方案所需计算量的对比，其中两个方案的代理签名算法与揭示代理者身份算法的计算量相同，在此不再详述。
表2 LHWM方案、YZ方案和改进方案的比较
从表2可以看出，改进方案比LHWM方案少了一个群加法运算，比YZ方案少了一个群乘法运算和一个群加法运算，所以改进后的方案减少了计算的复杂度。
4 结 语
本文分析了杨丽等人提出的代理数字签名方案，并给出了两个改进的数字签名方案，经安全分析表明，改进后的两个方案在具有高安全性的同时还具有高效率，降低了计算复杂度。
参考文献
[1] MAMBO M， USUDA K， OKAMOTO E. Proxy signatures for delegating signing operation [C]// Proceedings of the 3rd ACM Conference on Computer and Communications Security. New Dehi， India： ACM， 1996： 48?57.
[2] 张建中，马伟芳.椭圆曲线上的盲代理盲签名方案[J].计算机工程，2010，36（11）：126?130.
[3] 张建中，薛荣红，彭丽慧.一种基于身份的代理环签名方案[J].计算机工程，2011，37（17）：126?148.
[4] 洪璇，陈克非，万中美.简单的通用可组合代理重签名方案[J].软件学报，2010，21（8）：2079?2088.
[5] 刘树栋，梁向前，许金芳.安全有效的代理可验证加密签名方案[J].计算机工程与应用，2011，47（28）：77?79.
[6] SHUM K， WEIL V K. A strong proxy signature scheme with proxy signer privacy protection [C]// Proceedings of the Eleventh IEEE International Workshops on Enabling Technologies： Infrastructure for Collaborative Enterprises. Pittsburgh， Pennsylvania， USA： [s.n.]， 2002： 55?56.
[7] LEE Narn?Yih， LEE Ming?Feng. The security of a strong proxy signature scheme with proxy signer privacy protection [J]. Applied Mathematics and Computation， 2005， 161（3）： 807?812.
[8] 谷利泽，张胜，杨义先.一种新型的代理签名方案[J].电子与信息学报，2005，27（9）：1463?1466.
[9] 鲁荣波，何大可，王常吉，等.对一种新型代理签名方案的分析与改进[J].电子与信息学报，2007，29（10）：2529?2532.
[10] 杨丽，张建中.对一种新型代理签名方案的进一步分析和改进[J].计算机工程与应用，2013，49（22）：100?103.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 9:33:16