《提炼基本几何图形　加强几何有效教学》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

提炼基本几何图形　加强几何有效教学

范文

马瑞雅

《数学课程标准》在几何方面的学习要求学生“能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系，利用直观来进行思考”，在初中几何的学习中，计算、推理和证明的依据是概念和定理。而每一个概念、公理和定理总是对应着一个剔除了无关信息的直观图形，如：三角形的中位线是连接三角形两条边的中点的线段(概念)，三角形中位线平行于第三边且等于第三边的一半(定理)，与此对应的直观图形如图1所示；等腰三角形底边上的中线、高线和顶角的平分线三线合一(定理)，与此对应的直观图形如图2所示，显然，图1和图2没有人为设置障碍线段即无多余线段，是能完整而又全面反映上述两个定理内容所必需的最简图形，称像这种与概念、公理、定理相对应的最简直观图形为基本几何图形，是几何概念、公理和定理的载体，这样就建立了一个几何概念、公理或定理与基本图形的对应关系，可以由定理联想图形，也可以由图形联想定理，实现直观与抽象的有机转换。

欧氏几何与非欧几何的显著区别之一就是欧氏几何的计算和证明不能避开直观的几何图形进行纯逻辑推理。必须以直观图形为载体，在几何计算和证明的实践活动中，图形往往是纷繁复杂、千变万化的，从而使学生在解题过程中难以抓住图形的本质和重点，对题目所给信息不能正确提取和重组。找不到解决问题的突破口而无从下手或者思维混乱，这是造成学生觉得几何难学的主要原因，但是，任何一个复杂的几何图形都是由相关的基本图形所构建、整合而成的，也就是说一个几何题往往是多个知识点的有机整合，因此，对复杂图形进行合理分解从中分离出基本图形，然后根据基本图形去联想由图所对应的概念、公理或定理所需的条件以达到对题目所给条件的正确组合，可以为学生寻找解题的突破口提供线索，这种“模块化”的思维方式，可以有效防止无关信息干扰，快速凸显解题突破口。提高思维的敏捷性，所以在平面几何的教学中应该重视基本几何图形的提炼与应用。

有调查表明：83％的学生认为“几何较难”，其中因为几何概念多、定理和性质容易混淆的占31％，几何的入门学习中概念的学习尤其重要，因为他们是定理学习的基础，准确地识记概念和熟练地运用定理，这是“双基”的要求，在抓好“双基”的基础上，要努力培养学生解决问题的能力，培养创新精神，实践表明，运用几何基本图形教学，建立知识点和基本图形对应关系，由定理(或概念)联想图形，由图形联想定理(或概念)，实现直观与抽象的有机转换，促进学生几何思维能力和解题经验的发展，是提高几何教学质量的有效措施。

1重视概念，夯实基础，利用基本图形理解和记忆概念

几何的学习是从概念开始的，与定义、概念相对应的图形称为概念型基本图形，如下表1：

几何概念和代数概念的显著区别就在于几何概念以陈述性概念为主，且它的定义必须以直观图形为基础，所以，几何概念教学尤其要重视概念理解与基本图形的认知相结合，可以按如下步骤进行：画图；揭露本质；图形变式，

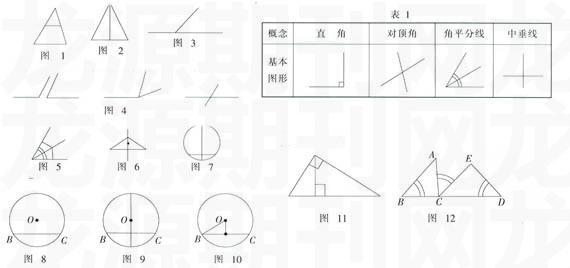
案例1邻补角的概念教学

第一步：给出相关情境，让学生从中感受邻补角：

第二步：从情境中提炼出基本图形，并让学生自己动手画出如下图3：

第三步：结合基本图形，揭露概念的本质；

第四步：图形变式，辨别真伪，如下图4：

学生通过情境感受邻补角，经历了画邻补角的过程，在交流中理解邻补角的概念，在变式中领悟和提炼基本图形，实现了图与概念的统一，也就能从复杂图形中识别出邻补角。

2立足定理，重视能力。利用基本图形破解解题思路

公理和定理的运用在推理中起决定性作用，与公理或定理相对应的图形称为定理型基本图形，例如：

(1)角平分线上的点到角的两边的距离相等，角的内部到两边距离相等的点在角的平分线上，如图5。

(2)线段垂直平分线上的点到线段两端点的距离相等，到线段两端点的距离相等的点在线段的垂直平分线上，如图6。

(3)垂直于弦的直径平分弦，并且平分弦所对的两条弧，如图7。

定理型基本图形较概念型基本图形要复杂得多。往往是多个概念性基本图形的有机整合，如果再把图形又置于复杂的几何综合题中。学生很难避开干扰图形看到问题的本质，导致解题困难，所以，定理型基本图形的提炼和反复操练十分重要，

案例2探究垂径定理

第一步：提供问题情境，如何将圆形纸片的一条弦平分(不借助工具)，见图8。

第二步：在活动中，让学生开动脑筋，思考起来，做起来。理解“折叠”的过程。

第三步：在交流中，老师与学生共同探讨“折痕”的本质，画出图形，如图9，并证明。

第四步：例题与练习，引导学生去发现计算和证明真正起决定作用的图形，如图10。

第五步：在练习的基础上进行经验总结，提炼出两种基本图形，如图9和图10。

提炼定理型基本图形建立了定理与图形的对应关系，定理图形化便于记忆，减少了记忆单元，便于从复杂图形中联想解决问题的相关知识点，利于复杂图形分解，打开解题思路。

因此，教师在几何定理教学中要让学生结合基本图形来掌握定理，加深学生对基本图形的认知，帮助学生建立图形与定理的密切联系，在引导学生对复杂图形进行拆积木式的分解过程中，能训练学生的识图能力，有利于能力的迁移。有利于在复杂图形中快速找到解题的思路。

3精练习题，总结经验，利用基本图形寻找解题规律

《数学课程标准》过程性目标要求：“学生在特定的数学活动中，获得一些初步的经验；参与特定的数学活动，在具体情境中初步认识对象的特征，获得一些经验……”学生在几何解题过程中，要善于去发现问题的共性，及时总结形成自己的经验。

在书本例题、习题和平时考试中经常出现的建立在同一图形结构上的几何题，他们所包含的部分几何图形的本质完全相同，称具有共同本质而出现频率较高的图形为经验型基本图形，例如：被删掉的射影定理及面积相等法。如图11所示；一对有用的相似三角形△ABC～△CDE，如图12所示。

几何问题是千变万化的，但是“万变不离其宗”!“熟能生巧”是几何学习的一条很有用的规律，巧的实质是理解其“宗”，所以，教师要在解题中不断引导学生进行解题回顾与反思，总结通法，明确算法流程，提炼解题所需的基本图形，有效促进解题思维定式的正迁移。从而提高解题效益。

几何教学实践表明，教师注重几何基本图形的提炼并训练学生运用几何基本图形来理解和记忆几何的定理与性质以至课本上的例题、重要习题，效果非常明显，记忆的准确性和牢固性都得到了很大改善，同时，几何图形的视觉记忆会随着不同的几何场景，进行定向回忆和自动提取。有效地促进迁移能力的形成，有助于打开解题思路，找到解题线索，提高解题速度，可以说，“一张基本图形胜似千言万语”。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。