《基于蒙特卡罗法的市场风险模拟研究》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

基于蒙特卡罗法的市场风险模拟研究

范文

宋辉

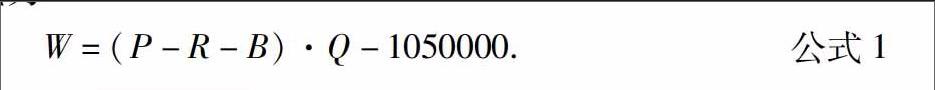
【摘要】基于概率分布的蒙特卡罗法是价格决策方法.新产品利润作为模拟对象，以Excel软件为基础工具，利用蒙特卡罗法进行模拟计算.可变成本、人工费、销售数量三个参数根据统计数据确定为离散分布、均匀分布和正态分布.RAND函数生成随机数共模拟利润1 000次，选择平均利润和亏损率两个参数作为销售价格的决策指标.模拟结果选择279元/件为销售价格，利润在0～150万元之间的频率是76.2%，亏损率6.8%，满足企业风险承担要求.为提高模拟精度，销售价格与销售量的相关关系需要进一步量化研究.

【关键词】概率分布；蒙特卡罗法；数学模拟；风险模型；概率决策

一、引言

某企业计划推出一款新产品，在经济下行、市场逐渐低迷的情况下企业担心市场风险.企业初步确定新产品三个不同的销售价格，新产品的固定成本已知，可变成本（人工成本单独）、预计销售数量都进行了市场调研，获取了统计数据.受企业委托，本文主要研究不同的销售价格下市场风险大小，为企业价格决策提供科学依据.

二、模拟方法

（一）蒙特卡罗法

蒙特卡罗方法是以概率统计理论为基础的数值计算方法，基本过程包括构造或描述概率过程、从已知概率分布抽样和建立模拟估计量三部分.蒙特卡罗法模拟结果是某型概率分布的随机变量，可用统计方法把分布的数字特征估计出数值解[1][2].

（二）模拟信息

本文涉及的概率构造包括三个参数，分别是可变成本、人工费、销售数量.模拟估计量是利润.

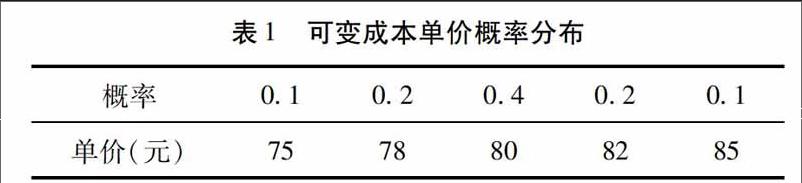
可变成本包括除人工費以外的零部件费用、电费、包装费等.企业一次进货量较大，进货间隔时间较长，可变成本数据较少，近三年价格数据服从离散型分布[3][4]，概率与单价见表1.

人工费是除固定成本中的人工外的可变成本中的人工工资、福利费等.人工费受市场影响波动不大，近三年价格数据分析，服从均匀分布，最大值80元/件，最小值60元/件.

产品需求根据企业市场调研，假设服从正态分布，均值15 000万件，标准差4 500.

此外，固定成本包括固定资产折旧、管理费、推广费等，合计105万元.

为方便编辑公式，设产品售价为P，人工费为R，可变成本为B，产品需求量为Q，利润为W.模拟估计量利润表达式为

三、模拟结果

本文计划进行1 000次模拟.

每次模拟中都需要随机产生概率输入量R、B、Q，以概率分布和随机数来确定概率输入量数值.随机数的发生概率等于输入量发生的概率[5].

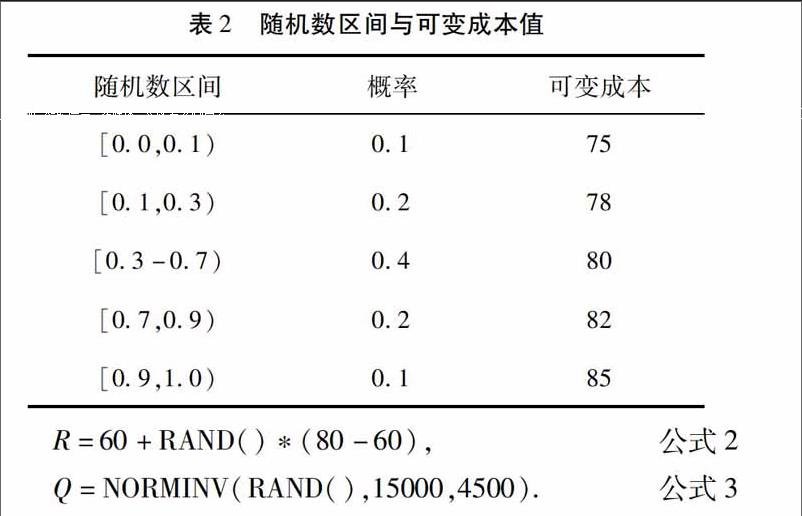
在Excel工作表中，以RAND函数生成随机数，值域为[0，1）.可变成本的随机数与概率对应关系见表2，利用Excel中VLOOKUP函数抓取数据.人工费成本与随机数的关系见公式2.需求量与随机数关系利用Excel中正态分布逆函数直接生成，见公式3.

四、决策分析

（一）销售价格选择

销售价格的选择指标采用平均利润和亏损率两个参数.表4显示平均利润由43.1万元提高到117.3万元.以15 000件计算总的可变成本为225万元，加上固定成本105万元，总成本是330万元，按此计算平均利润率分别为131%，27.7%，35.6%.标准方差随着销售价格的提高而逐渐提高，说明概率曲线越扁平，利润值越离散.亏损率随着销售价格的提高而逐渐减少，由17.6%下降到3.3%.

综合考虑上述因素，结合企业的风险承受能力，推荐销售价格为279元/件.按此价格销售，企业亏损风险是68%，平均利润91.4万元.

（二）利润分布直方图

对表3中的利润以50万为等份计算频率分布，利润服从正态分布，其中利润在50～100万元之间的频率是319%，利润在0～150万元之间的频率是76.2%.

（三）决策不足

本文在决策中存在三点不足.一是基础数据不足，其中可变成本数据量少，最后以离散型分布进行模拟.二是不同销售价格与销售量（产品需求量）之间的相关关系没有识别，本文以固定均值和标准差进行模型，一般不符合市场规律.本文尝试销售价格与需求量按线性负相关进行模拟[6]，279元/件也是亏损率最小的.三是在决策中考虑并计算了平均利润率，全部以15 000件计算，虽具有比较价值，但指标实际意义不大.

五、结论

1.蒙特卡罗法是以概率统计理论为基础的数值计算方法，可以进行企业市场模拟，用于企业决策.

2.产品的可变成本、人工成本、需求量的概率输入量数值以其概率分布和随机数来确定，以Excel软件为基础，构建模拟模型.

3.销售价格的决策依据采用平均利润和亏损率两个指标，根据企业承受能力选择279元/件为销售价格，按此价格，利润在0～150万元之间的频率是76.2%.

4.销售价格与销售量的相关关系没有识别是模拟的不足之处.本文主观假定销售价格与销售量按线性负相关进行模拟，279元/件也是亏损率最小的选择.

【参考文献】

[1]安德森，斯威尼.数据、模型与决策[M].北京：机械工业出版社，2015：339-375.

[2]柴洪，马竹书.基于蒙特卡罗模拟法的工程项目财务风险评估[J].项目管理技术，2012（11）：79-82.

[3]曲弘.基于不同函数的质量成本数学模型评析[J].辽东学院学报（自然科学版），2007（02）：103-106，113.

[4]颜清，彭小平.基于蒙特卡罗最小二乘的实验数据拟合方法[J].计算机与应用化学，2011（11）：1473-1476.

[5]王久胜，包卫军，胡杰.基于多维Gumbel Copula函数的投资组合VaR分析[J].数理统计与管理，2010（01）：137-143.

[6]崔伟群，杭晨哲.基于蒙特卡罗方法评定不确定度中相关随机变量模拟[J].现代测量与实验室管理，2010（04）：24-27.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。