《“等差数列前n项和”教学实录与反思》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

“等差数列前n项和”教学实录与反思

范文

林爱华

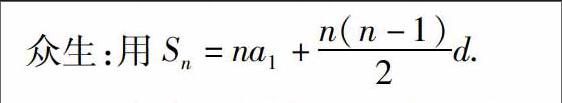
【摘要】本节课是必修5第二章第三节“等差数列的前n项和”的第一课时，主要内容是等差数列的前n项和公式的推导和简单应用.通过本课的部分教学实录谈谈对教学的几点反思.

【关键词】等差数列；前n项和；教学实录；反思

一、创设问题情境

问题1：1+2+3+4+…+100=？

师：大家都听说过高斯的故事吧，据说在200多年前，高斯上小学时，有一次数学老师给同学们提出了这样的一道问题：计算1+2+3+4+…+100=？当时高斯的同学一看到题目就马上埋头计算起来，而唯独他没有这么做，他先思考，结果当他的同学都在紧张计算却还没有得出答案的时候，他已经举手说：“老师，我做完了.”老师大吃一惊，原来是班上年纪最小的高斯.老师走到他身边只见他在笔记上写着5 050，不由得暗自称赞.同学们，你们知道小高斯当时用了什么妙法迅速解决了这个求和问题吗？

生1：他不是从左往右一个一个计算的.

生2：高斯发现1+100=101，2+99=101，3+98=101，…，50+51=101.因此，把1+2+3+4+…+100分成50组，每组和为101，共5 050.

师：回答得非常好！

1+2+3+4+…+100

=（1+100）+（2+99）+（3+98）+…+（50+51）

=101×50

=5050.

问题2：建筑工地上一堆圆木，从上到下每层的数目分别为1，2，3，…，9.共有多少根圆木？请用简便的方法计算.（数据小而少，学生很快就求得结果45）

问题3：求1到n的正整数之和，即1+2+3+…+n=？

（学生们纷纷模仿小高斯的做法来算，但很快就有学生算不下去了）

生3：老师，n是奇数还是偶数？

师：都有可能.（很快有学生说出了自己的想法）

师：很好，懂得对n分类讨论，要是不分类还有别的求和办法吗？

生5：把1+2+3+…+n各项顺序倒过来，即n+（n-1）+…+3+2+1，把两式相加再除以2即可.

师：回答得非常棒！刚才这名同学利用的是1+n=2+（n-1）=3+（n-2）=…=n+1这一特点求和.

二、课题引入

师：我们把a1+a2+a3+…+an叫作数列{an}的前n项和，记作Sn，如何求等差数列{an}前n项和Sn呢？

三、探究新知

师：设等差数列{an}的前n项和为Sn，则Sn=a1+a2+a3+…+an，能否用问题3的解决方法求和呢？请讨论并推导.（笔者下去巡查了一下，发现有的组讨论很激烈）

师：请一名同学说说你们组的讨论结果，是如何得到的？

师：不错，以上两个公式都是等差数列的前n项和公式，前者反映了等差数列的任意的第k项与倒数第k项的和等于首末项的和这个性质；后者反映了等差數列的前n项和与它的首项、公差之间的关系，并且是关于n的“二次函数”.华罗庚曾说过：“数少形不直观，形少数难入微.”你们能否认真观察公式（1）（2）并给予几何解释.（学生沉默了近1分钟，还是没有发现哪个图形与它们有联系）

练习热身：求下列等差数列{an}的前项和Sn（略）.

（这组练习目的是帮助学生熟悉公式，并能恰当地选择合适的公式）

四、应用举例

例1（教材第43页例1）（让学生阅读并审题）

师：根据题意求这10年资金的总投入即把这10年的资金相加，而每年投入的资金是多少？

众生：2001年是500万元，以后每年的投入资金比上一年增加50万元.

师：这是怎样的一个求和问题？

众生：等差数列，求以500为首项，以50为公差的等差数列的前10项和.

师：很好.要用哪个求和公式？

（分析完毕，利用幻灯片给出解题过程）

例2（教材第43页例2）（让学生阅读并审题）

师：要确定等差数列的前n项和的公式，最基本的量有哪些？（学生回顾等差数列的前n项和的公式，明确a1与d是等差数列的两个基本量，利用方程组思想解决）

五、练习巩固（略）

六、教后反思

（一）对教学过程设计的反思

本节开头以大家熟知的小高斯的故事设置情境，既激发学生的学习兴趣，同时也激励学生认真学习，浅显的引入让学生情绪高涨.这时又抛出第二个工地上木头的堆放问题，层层铺垫，引导学生从特殊到一般归纳等差数列的前n项和的推导方法，并得出结论Sn=n（a1+an）2，由an=a1+（n-1）d，进一步得到Sn=na1+n（n-1）2d.并且利用梯形面积帮助学生记忆等差数列的前n项和的两个公式.在推导出等差数列的前n项和之后就是应用举例，由于刚刚认识等差数列的前n项和公式，本人认为如果直接讲解教材中的例1，难度较大，于是补充了三道练习，根据所给的条件求等差数列的前n项和.目的是让学生熟悉公式，并能恰当地选择合适的公式.最后讲解教材中的例题1、2.这样的安排符合了学生的认识规律，由易到难，层层递进，在练习巩固部分，通过变式，让学生体会“思则变，变则通”的理念，同时体验到方程组思想在解题中的运用，加深理解等差数列的前n项和公式中五个变量a1，an，n，d，Sn，只要知道其中三个就可求另外两个，即“知三求二”.

（二）对学生评价的反思

在整个教学过程中，本人很重视学生的质疑与回答.如果对了，本人及时给予肯定，这样可以鼓励他们继续积极思考并回答问题.值得一提的是在教学过程中本来并没有预设学生对问题3的解决会采用分类的方法进行分组求和，当学生提出疑问n是奇数还是偶数时，笔者没有直接否定他的做法而是耐心引导，及时肯定，给他留出足够的计算时间，使他能够顺利完成1+2+3+…+n求和，并发现不论n为奇数还是偶数，和都为n（n+1）2.当笔者及时肯定他的发现时，他表现出少有的兴奋，目光更有神了，听课更专注了.虽然上课的时间较有限，但如果当时笔者假装没听见不予理睬的话，那可能将会是另外一种情形，学生会感到被教师所冷落，对他的回答不关心，从而会影响他学习数学的积极性.总之，在课堂中对学生的评价要及时，多用赏识的眼光看待他们.

（三）对教学中不足的反思

由于对等差数列的前n项的公式的推导花费的时间稍多了一些，而导致最后的变式训练和小结有些仓促.如果重新设计教学的话，笔者会适当减少练习.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。