《基于Spark平台的多皇后问题并行求解》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

基于Spark平台的多皇后问题并行求解

范文

摘要：针对传统运行于单机上的多皇后问题求解算法计算效率低的问题，本文基于分布式计算平台Spark，设计了一种集群环境下的多皇后问题求解并行化方案，实现了利用集群资源求解多皇后问题的并行算法。对回溯法进行了改进，有效的缩小解空间。

关键词：并行计算;Spark;多皇后问题;回溯法

N皇后问题是计算方面的一个经典的NP难问题，它的特点是随着皇后数目N的增加，计算时间呈指数增长。对于高位数的皇后问题求解，传统的串行求解算法往往无法再可接受的时间内完成。然而，单机上的运算资源是有限的，基于单机多核的并行解决方案，并不能从保证能求的高位数皇后问题的解。本文基于分布式计算平台Spark，采用经典的回溯法，设计了一种集群环境下的多皇后问题求解并行化方案，实现了利用集群资源求解多皇后问题的并行算法。

1.回溯法求解多皇后问题

回溯法在求解N皇后问题时，以深度优先的顺序对各个棋盘节点进行选择判断。用基本的经典回溯法算法得到多皇后问题的全部有效解，需要对整个解空间进行搜索。当皇后问题的皇后个数n增大时，整个解空间的规模大约是n*n！，搜索的效率非常低。若把N*N的棋盘放置到一个二维数组时，n皇后问题有效解数的指数递增性质，随着皇后个数的增加，需要的比较时间也会大规模增长。所以需要对基本回溯法进行改进，对其进行一定的改进和剪枝，减小回溯的解空间，减少比较次数。

2.1对基础回溯法的改进

由于N皇后问题在使用基础回溯算法时，会有比较次数和计算量过大的问题，特别是随着皇后个数的增加，一丝微小的差别可能就会被无限放大。针对这些问题，本文在参考了文献[2，3，4]中的改进方法后，对多皇后问题的基础回溯算法进行了一些改进的探讨。

2.2.1储存数据结构的改变

文章将采取用一个一维数组来存放一个有效解空间树分支，也就是说用一个一维的数组储存一个有效解。主要优点有

第一：可以减少储存空间，显而易见一个一维N位长的数组只有一个N*N二维数组N分之一的存储空间;

第二：可以省去行冲突，多皇后问题一共有三种冲突：行、列、斜线。

第三：可以减少比较的次数。

2.2.2减少需要探测的放置点

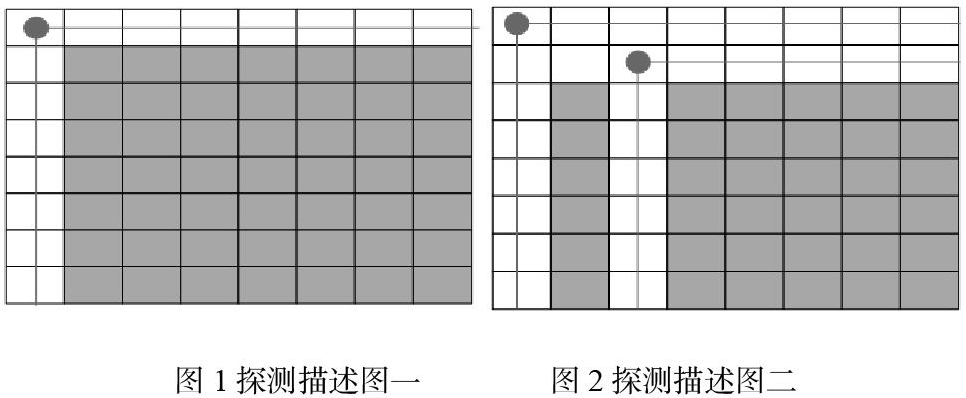
对于回溯法解决多皇后问题，随着N的个数的增长，需要探测的位置放大，且随着解空间树的增加，这一探测比较被明显放大且随着解空间树的增加，这一探测比较被明显放大，如四皇后问题一个解需要探测16个位置，有4的4次方个比较次数，而八皇后问题便需要探测64个位置，有8的8次方个比较次数，采用的是避免行列的冲突比较，即如果一个皇后成功放置以后，它所在的行和列即锁定，不再进行探测。通过比可以发现，完全可以避免一些不必要的探测，如放置一个皇后后，它所在的行和列完全可以不再进行探测，即缩小了它的棋盘放置空间。这里我采用的是避免行列的冲突比较，即如果一个皇后成功放置以后，它所在的行和列即锁定，不再进行探测。如图1所示，放置第一个皇后后，进行行和列的消除后，便成了7*7的范围。

放置第二个皇后后如图2，第三个皇后的放置便成了6*6的范围，比原来又少了一行和一列的探测范围。

2.2.3利用棋盘对称性减小解空间

棋盘是对称的，对任意有效解的多皇后放置图进行合理的旋转也会得到一个有效解。结合分枝限界法对解空间进行一个大幅度的剪枝操作，可以极大的缩小解空间范围。

由此特征，在多皇后问题上，可以得到以下两个特征：

（1）对于多皇后问题，棋盘上的每一种合理放置，经过有限次的水平，顺时针，逆时针翻转，仍然是一个有效的放置解法。

（2）对于多皇后问题，如果用result[i]表示合理布局中以i为第一个位置的布局的数量，则有这样的一个等式：result[i]=result[n-i+1]。

在对多皇后问题的布局搜索时，可以利用对称性的原理来减少一半的解空间状态树分支。利用布局的水平翻转，对解空间进行优化，大概能提升一倍左右的效率（也就是减少50%左右的分支）。下面将对改进方法进行具体的解释。

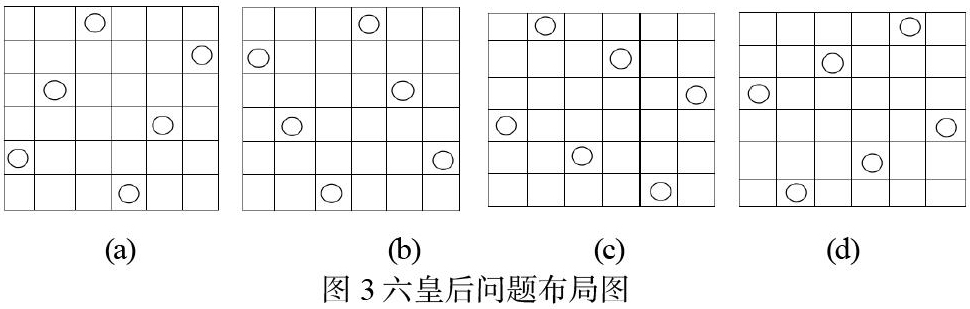
以6皇后问题为例，6皇后问题共有4个有效解，布局图如下：

通过图可以发现，图4（a）和图4（b），图4（c）与4（d）是左右对称的，相当于旋转了180度。进过分析，偶数个数的多皇后的放置问题，仅仅可以搜索以前2/n列为起始位置的解空间，若搜索到有效解，直接进行水平翻转，得到后面的解，且不发生冲突。如果是奇數个数的多皇后的放置问题，对于最中间一列为起始位置有效解来说，直接进行翻转，会造成重复解的问题。

因此，对多皇后问题的个数进行判断，如果皇后个数n为偶数，则直接只搜索以第一行前n/2列为初始位置的解空间，然后对搜索到的合理布局进行水平翻转，得到对称布局。如果n为奇数，则搜索前2/（n+1）列，但是如果是第2/（n+1）列，则不对其搜索到的合理布局进行翻转。

3多皇后问题并行化设计

为了并行实现多皇后问题的回溯解法，需要的是对该任务进行分解，将其分解成多个任务，然后，再将小的任务划分到各个分节点上面，当分节点计算完毕后，再将计算结果整合在主节点中。采取平均划分法，根据用户输入的需要求解的多皇后问题的皇后个数而分配任务。对于每一个分任务，会根据其首位置放置，对该分支的解空间进行回溯法搜索，然后对相应合理进行水平翻转处理并记录，最后返回结果给主节点，完成自己部分的计算。

在数据结构方面采用了一个N*N的二维数组表示（N代表皇后个数），但这个二维数组是N个任务共用的，每个任务用一个N维数组。此外，采用集合列表这种数据结构来与数组进行对比，并解决一些并行输出顺序可能混乱的问题。

4实验结果与分析

实验需要的Spark集群环境在虚拟机中搭建，集群中共3台虚拟机（其中主节点1台，从节点2台），各虚拟机配置信息见表1。集群节点操作系统为CentOS 6.6，安装有JDK 1.8，本文算法的实现基于Spark-2.1.1版本。

本文实验分别在启用了集群的1个工作节点（Spark集群单节点）和2个工作节点情况下进行，并与采用回溯法的传统求解算法进行对比。实验结果如表2所示。

从运行时间对比图7可以看出：（1）在皇后数目较少时，多皇后问题并行求解算法与传统的方法在计算效率上差别不明显，因为集群内部节点间通信需要消耗一定的时间。（2）随着皇后数目的增多，基于Spark平台的并行求解方法的优势会更突出。

5结论

文章基于分布式计算平台Spark，设计了一种集群环境下的多皇后问题求解并行化方案，实现了利用集群资源求解多皇后问题的并行算法。对多皇后问题求解选取出可求出全部解的回溯法，并對该方法进行了改进，从而有效的缩小解空间。最后，通过实验验证了设计的多皇后问题并行求解算法的正确性，同时该方法具有高效的计算能力和较好的扩展特性。

参考文献：

[1]郑光勇徐雨明罗振庭. 基于混合化学反应优化算法的N皇后问题研究 [J]. 数字技术与应用，2019，37（9）：116.

[2]鲍康胜. 从八皇后问题引发递归回溯算法的思考[J]. 电脑编程技巧与维护.2019，（5）： 32-34.

[3]原慧芳，于慧敏.改进回溯算法实现N皇后问题求解[J].电脑编程技巧与维护，2016（12）：15-16+34.

[4]王宁. 应用蚁群算法求解N皇后问题[J]. 现代交际：学术版.2016，（5）：245-246.

[5]叶均隆叶均明余伟红.? 图像思维解释八皇后算法及其拓展问题[J]. 无线互联科技. 2018， 15（22）： 106-107.

[6]姜学军.武枫.黄海新.Spark大数据计算平台[J]. 电子世界. 2018，（15）：82-84.

作者简介：

代新晓（1986年3月），女，辽宁省东港市，硕士研究生，讲师，研究方向：计算机网络、大数据.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。