网站首页  词典首页

请输入您要查询的论文：

　

标题 农业面源污染与农业经济增长的空间互动效应
范文 梁伟健 江华 廖文玉 秦明



摘要：基于2004—2015年省级面板数据，运用空间联立方程模型分析农业面源污染与农业经济增长的空间互动效应。实证结果显示：农业面源污染与农业经济增长之间相互影响，并且均存在空间溢出效应。亩均总氮排放量、亩均总磷排放量分别与亩均农业产值之间呈现显著“N型”曲线关系，而且，考虑空间溢出因素后，“N型”关系转折点的作用区间收窄。鉴于此，应当积极调整种植结构，降低粗放生产方式对环境的破坏，同时，从区域协调发展的角度，统筹农业经济的增长和环境污染的治理，避免出现短板效应，实现农业可持续发展。
关键词：农业面源污染；农业经济增长；空间溢出；空间联立方程
中图分类号：F32 文献标志码：A 文章编号：1001-862X（2018）03-0034-009
一、引 言
改革开放近四十年，中国农业综合生产能力显著提高，利用不到世界10%的耕地养活了世界近20%的人口。与此同时，农业发展带来了严重的面源污染问题。第一次全国污染源普查公报显示，农业源主要水污染排放量为化学需氧量1324.09万吨、总氮270.46万吨、总磷28.47万吨，分别占全国总排放量的43.71%、57.19%和67.27%，而且呈现逐年增加的态势。与此同时，水土流失情况也不容乐观。第一次全国水利普查结果显示，31.12%土壤遭到侵蚀。那么，随着农业经济的持续增长，环境污染有改善的可能吗？特别是，随着全球化进程的推进以及市场化改革的深入，区域协同发展成为必然，空间要素又对环境污染格局带来哪些新的挑战？
事实上，Ehrlich 和Holdren（1971）[1]最早提出环境影响模型（IPAT），从人口、富裕程度以及技术三个方面论述对环境的影响，但该模型无法反映非线性的变化。[2]基于此，Dietz和Rosa（1994）[2]引入随机因素将模型拓展为STIRPAT，从而提供了可行的实证分析框架。其后，大量学者围绕该模型进行实证研究，探讨了经济增长对环境的影响。[3][4]就影响方式而言，Grossman和Krueger（1995）[5]发现经济增长与环境污染之间也存在类似库兹涅茨曲线倒U型的特征：随着经济的增长，环境污染会不断恶化，但经济发展到一定阶段以后，环境开始得到改善。López， （1994）[6]、Andreoni和Levinson （2001）[7]等学者从理论上证实了该假说的合理性，国内学者利用农业污染数据也都证实了环境EKC假说成立【8]-[10]。此外，新近的研究尝试将两种方法结合起来，更加深刻地探讨经济增长和环境污染之间的非线性关系。[11[12]然而，上述方法都将环境污染作为外生变量考察[13]，忽视了其对经济增长的反作用，无法摆脱互为因果关系的内生性困扰。
与此同时，越来越多的学者注意到，忽视环境污染与经济增长的空间溢出因素会导致估计结果偏误。鲁庆尧和王树进（2015）[14]基于地理空间因素，对农业经济活动的空间相关性进行分析，并利用空间计量模型证实我国省域经济环境指数存在较强的空间依赖性以及正的空间溢出效应。沈能和王艳（2016）[15]则以EKC为分析框架，采用空间面板计量模型考察农业环境EKC特征及空间效应，并证实农业污染呈现空间集聚。与上述分析不同，吴义根等（2017）[16]基于STIRPAT分析框架，利用空间面板计量模型分析农业面源污染的影响因素，并证实农业经济增长的直接效應和空间溢出效应均具有正向影响。虽然上述研究考虑到了空间溢出在经济增长影响环境污染过程中的作用，但同样，忽视了环境污染的内生性作用，从而导致估计结果存在偏误。
综上所述，已有研究存在以下两个方面的问题：第一，往往割裂了STIRPAT与EKC之间的关系，事实上，通过将两者进行结合，能够更有效地刻画农业经济增长与农业环境污染之间的关系，已有学者做出了有益的尝试；第二，往往将环境作为外生变量来考察，而忽略了环境与经济之间的互为内生关系，特别是从空间溢出角度进行考察。鉴于此，本文试图在以下两个方面进行拓展：首先，在分析框架上，本文将结合STIRPAT与EKC，从而更加深刻地探讨农业环境污染与农业经济增长之间的关系；其次，在实证策略上，本文将从环境污染内生的视角出发，运用空间联立方程模型，对农业经济增长与农业环境污染的空间溢出与空间互动关系进行考察。
二、数据来源及变量说明
本文数据来源于2004—2015年《中国统计年鉴》和《中国农村统计年鉴》30个省域层面面板数据，鉴于西藏特殊的资源禀赋，并未纳入研究。选择2004年作为研究的起点主要是考虑到从2004年实施逐步减免农业税，并对农户进行相关补贴，农业生产的政策环境发生重大变化。与此同时，颜廷武等（2014）[17]指出，总量指标容易受到农业生产规模影响，不利于年际间纵向对比，而人均指标缺少数据支撑，农林牧渔各产业之间划分较为困难，容易造成偏差，相较之下，强度指标可以进行年际间纵向对比，还能消除复种指数影响，使得地区间比较更加公平合理。鉴于此，本文亦采用强度指标进行衡量。
首先，农业面源污染指标，本文选择农业化肥污染作为表征，主要理由如下：一方面，化肥过量施用是造成农业面源污染的重要来源之一，另一方面，农业化肥面源污染主要是指化肥过量和不合理施用使得化肥营养物质流失并导致地表水富营养化和地下水硝酸盐污染。[18]以氮肥为例，未被吸收的氮肥会以氮素的形势进入环境，导致地表水富营养化，地下水硝酸盐富集和酸雨形成，同时通过化学反应进入空气中。[19][20]因此，本文主要以总氮（TN）、总磷（TP）表征农业化肥面源污染。目前，农业面源污染的评价方式主要包括单元调查法[21][22]、代理变量法[23]、模型模拟[24]等。鉴于数据可得性，本文采用单元调查法，并结合第一次全国污染源普查《化肥流失手册》对农业面源污染进行匡算。本文所考察的农业化肥污染，主要来源于农业种植过程中化肥过量施用，因此，本文选择农业产值作为农业经济增长的表征，并利用总产值指数进行平减，剔除时间价值的影响。值得注意的是，鉴于选择不同污染指标，EKC关系会呈现出“U型”关系、“N型关系”和“倒N型”关系等。[25]因此，本文同时使用农业产值的二次项和三次项，捕捉可能存在的关系。
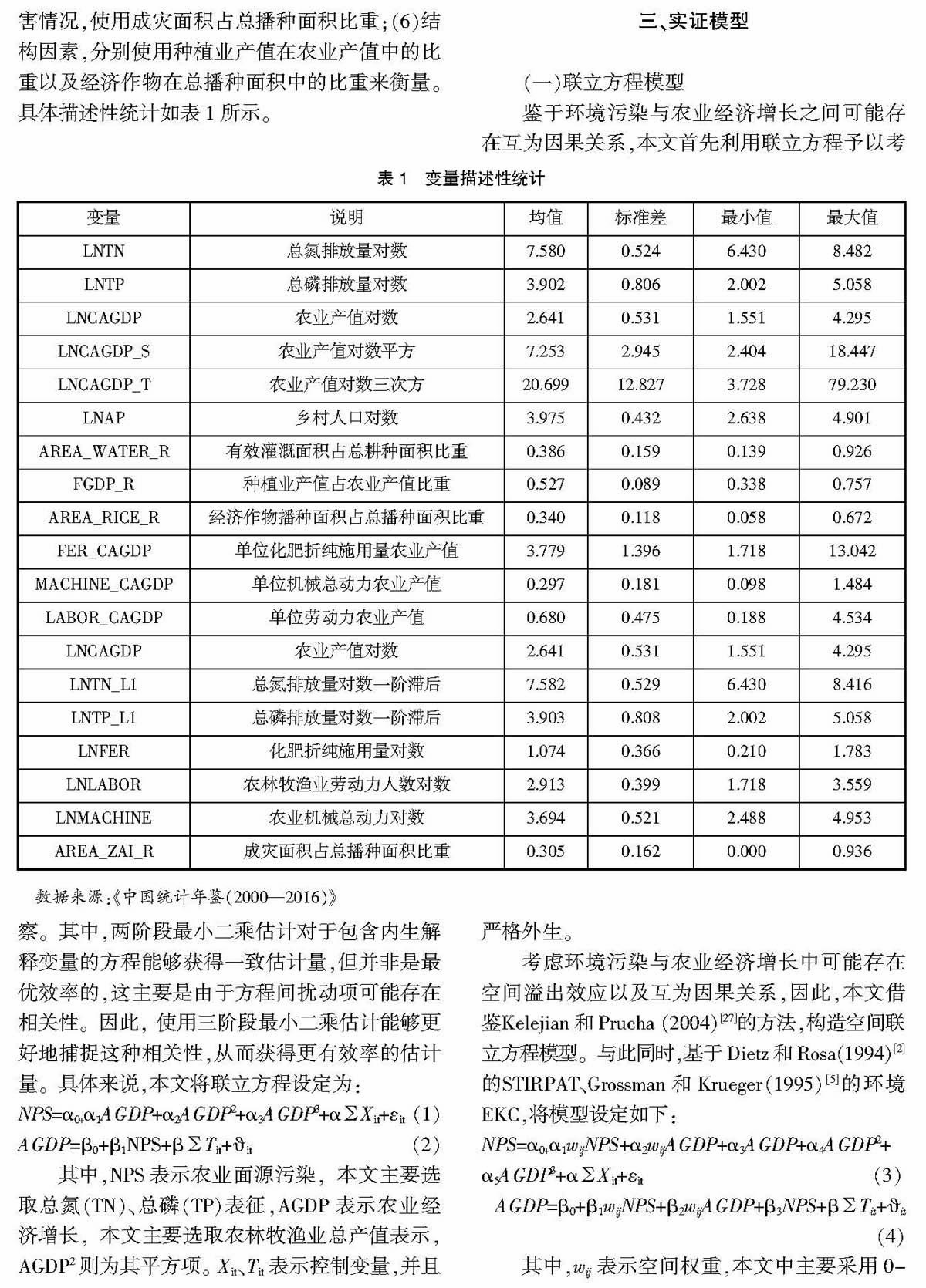
其次，解释变量方面。在环境污染方程中，根据STIRPAT分析框架，本文选取乡村人口作为人口表征； 技术进步方面，一方面是技术效率，主要使用单位化肥投入、单位机械投入以及单位劳动力投入带来的农业产值；另一方面是结构指标，主要考察种植业产值在农业产值中的比重以及经济作物在总播种面积中的比重。除此之外，考虑到化肥施用过程中，灌溉技术对促进化肥吸收具有十分重要的作用，因此，本文选择可灌溉耕地面积占总面积的比例作为灌溉技术的表征。在经济增长方程中，本文参照孙圣民和陈强（ 2017）[26]，选择如下指标作为农业投入变量：（1）劳动投入，以农林牧渔总劳动力计算，单位为万人；（2）化肥投入，以化肥施用折纯量表示；（3）农业机械投入，以农业机械总动力表示；（4）灌溉水平，使用有效灌溉面积占总耕地面积的比重，以此衡量抵御自然灾害天气对农业生产影响的能力；（5）自然灾害情况，使用成灾面积占总播种面积比重；（6）结构因素，分别使用种植业产值在农业产值中的比重以及经济作物在总播种面积中的比重来衡量。具体描述性统计如表1所示。
三、实证模型
（一）联立方程模型
鉴于环境污染与农业经济增长之间可能存在互为因果关系，本文首先利用联立方程予以考察。其中，两阶段最小二乘估计对于包含内生解释变量的方程能够获得一致估计量，但并非是最优效率的，这主要是由于方程间扰动项可能存在相关性。因此， 使用三阶段最小二乘估计能够更好地捕捉这种相关性，从而获得更有效率的估计量。具体来说，本文将联立方程设定为：
NPS=α0+α1AGDP+α2AGDP2+α3AGDP3+α？蒡Xit+εit（1）
AGDP=β0+β1NPS+β？蒡Tit+it（2）
其中，NPS表示农业面源污染，本文主要选取总氮（TN）、总磷（TP）表征，AGDP表示农业经济增长，本文主要选取农林牧渔业总产值表示，AGDP2则为其平方项。Xit、Tit表示控制变量，并且严格外生。
考虑环境污染与农业经济增长中可能存在空间溢出效应以及互为因果关系，因此，本文借鉴Kelejian和Prucha （2004）[27]的方法，构造空间联立方程模型。与此同时，基于Dietz和Rosa（1994）[2]的STIRPAT、Grossman和Krueger（1995）[5]的环境EKC，将模型设定如下：
NPS=α0+α1wijNPS+α2wijAGDP+α3AGDP+α4AGDP2+α5AGDP3+α？蒡Xit+εit （3）AGDP=β0+β1wijNPS+β2wijAGDP+β3NPS+β？蒡Tit+it （4）
其中，wij表示空间权重，本文中主要采用0-1相近的地理权重。wijAGDP表示邻近地区农业经济增长对本地区的空间溢出影响，wijNPS表示邻近地区农业面源污染对本地区的空间溢出影响。Xit和Tit分别表示控制变量。
（二）空间权重
空间权重衡量了区域之间的空间距离，是空间计量模型设定的关键。鉴于环境污染问题具有很强的区域关联特性，主要采用两种权重设定方法，尽量克服权重设定偏误带来的误差。一是0-1相邻权重，即根据30个省市之间是否存在相鄰边界来进行划分，存在共同边界则为1，否则为0，其中，将海南设定为与广东省和广西省相邻。二是地理权重，将其设定为：wij=1/dij。其中，dij表示各省份省会城市或者直辖市经纬度的欧氏距离。
（三）Morans I检验
在使用空间计量模型前，需要对数据的空间依赖性进行考察。本文借鉴Moran（1950）[28]方法，利用Morans I对变量中的空间自相关进行全域检验，其原假设为变量间不存在任何形势的空间相关性，具体设定如下：
I=■
其中，S2=■为样本方程，Morans I取值一般在-1到1之间，大于0表示正相关，即高值与高值相邻，低值与低值相邻；小于0表示负相关，即高值与低值相邻。
四、实证结果
（一）基准回归
本文分别进行OLS、2SlS、3SLS及其迭代回归，估计结果如表2所示。污染方程结果显示，农业经济增长的一、二、三次项均通过了1%显著性水平的检验，而且，系数方向满足N型曲线特征，即随着农业经济的不断增长，农业化肥污染呈现先增加、后减少然后再增加的N型特征，两个转折点依次为亩均706元、1814元。目前，中国农业产值正逐步由第一转折点向第二转折点过渡，需要警惕农业经济增长带来的环境压力，采取积极措施应对。与此同时，通过比较工具变量法和普通回归结果可知，两者结果相差较大，而工具变量法之间的差别不大。因此，如果忽略农业经济增长与污染之间的互为因果内生性关系，会造成估计结果的偏误。事实上，这一结论也可以从污染方程中得到佐证。农业化肥污染及其1阶滞后项通过了相关显著性检验，意味着农业化肥污染对农业经济增长存在显著的影响。
鉴于农业经济增长与农业化肥污染可能存在空间溢出特性，本文分别进行Morans I检验，估计结果如表3所示。结果显示，农业经济增长与农业化肥污染均通过了1%显著性检验，即均存在空间溢出特征。因此，如果忽略这种空间溢出关系，也会导致模型估计结果的偏误。
本文使用空间联立方程模型在考察农业经济增长与农业化肥污染互为内生关系的基础上，考虑空间溢出的影响，并分别利用相邻权重和地理权重进行回归，以确保估计结果稳健，具体结果如表4所示。从方程拟合程度来看，空间联立方程模型相较于普通联立方程模型有了较大提升，这表明，前者拟合效果更好，应该考虑空间溢出因素的影响。与此同时，总氮排放量和农业经济增长的空间溢出效应均通过了1%显著性检验，这也就意味着，如果忽略空间溢出效应会造成模型估计的偏误。因此，无论是从模型拟合程度上来看，还是从变量显著性角度来看，空间联立方程的确更加适合本文的研究。
首先，从污染方程来看。总氮排放量和农业经济增长的空间溢出效应分别显著促进和抑制本地区总氮排放量，并且从作用效应来看，前者更为明显。显然，环境污染具有负外部性，会加剧周边地区的污染，而农业经济增长的作用则可能通过溢出效应，提高本地区的化肥利用效应。与此同时，考虑空间溢出效应后，农业经济增长对农业化肥污染的作用也发生了分化，经过测算，相邻权重获得两个转折点分别调整为750元、1494元，地理权重获得的两个转折点分别为716元、1659元。这表明，在空间溢出作用下，第一转折点推后而第二转折点提前。可能的解释是，空间溢出改变了农业环境污染和农业经济增长的作用尺度：一方面，环境污染存在溢出效应，周边地区农业化肥污染会在提高本地区污染程度的同时降低农业经济增长，从而延缓了调整农业生产方式，降低化肥使用的紧迫性程度；另一方面，农业经济增长也存在溢出效应，周边地区农业经济的发展会促进本地区农业经济和环境污染的增加，提高了种植结构调整的动力，从而加剧了化肥的过量施用。除此之外，从控制变量来看，人口强度、化肥使用效率以及机械使用效率强度均正向促进总氮污染物的排放，而劳动生产率则表现为显著的抑制作用。
其次，从产出方程来看，总氮排放量和农业经济增长的空间溢出效应均通过了1%显著性水平的检验，这也就意味着，周边地区总氮污染物和农业经济增长分别抑制和促进本地区农业经济增长，这主要是由于两者分别具有负外部性和正外部性造成的。这也再次说明，需要关注农业化肥污染对农业经济增长的负向作用，如果忽略这种反向关系，会造成模型估计的偏误。在控制变量方面，粮食作物产值占比、总氮排放量的一阶滞后项、受灾情况以及劳动力投入均会显著抑制农业产出，而经济作物占比、化肥投入以及机械投入会显著促进农业经济增长，符合一般常识。
（二）稳健性分析
本文使用总磷排放量作为农业化肥污染物的表征，运用空间联立方程考察农业化肥污染与农业经济增长之间的空间互动效应，并同时提供相邻权重和地理权重估计结果，具体结果如表5所示。同样，总磷排放量和农业经济增长的空间溢出效应均通过了1%显著性检验，这意味着，如果忽略空间溢出效应会造成模型估计的偏误。首先，从污染方程来看。总磷排放量和农业经济增长的空间溢出效应分别显著促进和抑制本地區总磷排放量，并且从作用效应来看，前者更为明显，与上述结论一致。而在考虑空间溢出效应后，农业经济增长对农业化肥污染的作用转折点也发生了变化，相邻权重获得两个转折点分别调整为812元、1480元，地理权重获得的两个转折点分别为902元、1347元。同样，在空间溢出作用下，第一转折点推后而第二转折点提前，与上述结论一致。这也再次表明，空间溢出效应作用不容忽视。在控制变量方面，人口强度、化肥使用效率以及机械使用效率强度均正向促进总氮污染物的排放，而劳动生产率和粮食作物产值占比则表现为显著的抑制作用，与上述结论一致。
其次，从产出方程来看，总磷排放量和农业经济增长的空间溢出效应均通过了1%显著性水平的检验，这也就意味着，周边地区总氮污染物和农业经济增长分别抑制和促进本地区农业经济增长，这主要是由于两者分别具有负外部性和正外部性造成的，与上述结论一致。这也再次说明，需要关注农业化肥污染对农业经济增长的负向作用，如果忽略这种反向关系，会造成模型估计的偏误。在控制变量方面，粮食作物产值占比、总氮排放量的一阶滞后项、受灾情况以及劳动力投入均会显著抑制农业产出，而经济作物占比、化肥投入以及机械投入会显著促进农业经济增长，与上述结论一致。
五、主要结论与政策建议
经济增长与环境污染之间的关系是经济学的重要命题，特别是，随着中国经济进入新常态，调整供给侧结构性矛盾刻不容缓，实现经济可持续发展，提高经济发展质量。与已有研究往往忽视环境与增长之间互为内生的因果关系以及空间溢出作用不同，本文运用空间联立方程模型，同时考察上述两种效应，以期更为准确地刻画两者之间的关系。本文的主要结论如下：第一，农业化肥污染与农业经济增长之间存在互为内生关系，割裂其一必将导致估计结果的偏误，而且，随着农业经济增长的发展，农业化肥污染呈现先增加、后减少然后再增加的N型特征；第二，农业经济增长和农业化肥污染均存在空间溢出效应，而且前者能够促进产出抑制污染，后者的作用则恰好相反，从而使得“N”型曲线转折点收紧；第三，随着人口强度、化肥使用效率、机械使用效率的提高，劳动生产率、粮食作物产值占比的降低，农业化肥污染将增加，而随着经济作物播种面积占比、化肥投入、机械投入的增加，粮食作物产值占比、滞后一期的农业化肥污染排放量、劳动力投入以及自然灾害发生占比的降低，农业经济增长将提高。
本文的研究具有以下政策含义：一是调整农业种植结构，提升农产品品质，实现农业可持续发展。农业经济增长与环境污染之间相互影响、相互作用，并不是非此即彼的关系，一方面，随着经济的增长，环境污染也可能随之下降，从而同时实现经济与环境效益；另一方面，需要警惕经济持续增长带来的环境压力，这主要是由于种植结构的调整，农户进行经济作物种植从而提高收入的迫切需求所造成的。因此，应当积极调整种植结构，降低粗放生产方式对环境的破坏，提高农产品品质，从而获得可持续发展。二是统筹区域发展，促进区域协调发展。农业经济的增长和环境的污染均存在空间溢出效应，如果忽视这种效应将加剧地区间发展的不平衡，也最终导致整体发展的不协调。因此，需要从区域协调发展的角度，统筹农业经济的增长和环境污染的治理，避免出现短板效应。三是加大农业科技投入，推进农业机械装备制造业转型升级，缓解农业供给侧结构性矛盾。上述结论显示，农用机械、化肥以及劳动力等农业生产要素的产出效率也是影响农业面源污染和农业经济增长的重要因素，通过提高这些要素的产出效率可以实现在降低农业污染的同时，促进农业经济发展。因此，需要通过提高农业科技投入，促进农业装备制造业转型升级，实现农业从粗发投入到高质量发展的转型，缓解农业供给侧结构性矛盾。
参考文献：
[1]Ehrlich， P. R.， Holdren， J. P. Impact of Population Growth[J]. Science， 1971， 171（3977）：1212-1217.
[2]Dietz， T.， and Rosa， E. Rethinking the Environmental Impacts of Population， Affluence and Technology[J]. Human Ecology Review， 1994， 1（2）， 277-300.
[3]Hilton F G H， Levinson A. Factoring the Environmental Kuznets Curve： Evidence from Automotive Lead Emissions[J]. Journal of Environmental Economics and Management. 1998， 35（2）： 126-141.
[4]Selden T M， Song D. Environmental Quality and Development： Is There a Kuznets Curve for Air Pollution Emissions？[J]. Journal of Environmental Economics and Management. 1994， 27（2）： 147-162.
[5]Grossman G M， Krueger A B. Economic Growth and the Environment[J]. Nber Working Papers. 1995， 110（2）： 353-377.
[6]López R. The Environment as a Factor of Production： The Effects of Economic Growth and Trade Liberalization[J]. Journal of Environmental Economics & Management. 1994， 27（2）： 163-184.
[7]Andreoni J， Levinson A. The simple analytics of the environmental Kuznets curve[J]. Journal of Public Economics. 2001， 80（2）： 269-286.
[8]李太平，张锋，胡浩. 中国化肥面源污染EKC验证及其驱动因素[J]. 中国人口·资源与环境， 2011， 21（11）： 118-123.
[9]陈勇，冯永忠，杨改河. 陕西省农业非点源污染的环境库兹涅茨曲线验证[J]. 农业技术经济，2010（7）： 22-29.
[10]田素妍，郑微微，周力. 中国畜禽養殖业低碳清洁技术的EKC假说检验[J]. 中国人口·资源与环境，2012， 22（7）： 28-33.
[11]York R， Rosa E A， Dietz T. A rift in modernity？ assessing the anthropogenic sources of global climate change with the STIRPAT model[J]. International Journal of Sociology & Social Policy. 2003， 23（10）： 31-51.
[12]林伯强，蒋竺均. 中国二氧化碳的环境库兹涅茨曲线预测及影响因素分析[J]. 管理世界，2009，（4）： 27-36.
[13]曹大宇，李谷成. 我国农业环境库兹涅茨曲线的实证研究——基于联立方程模型的估计[J]. 软科学， 2011， 25（7）： 76-80.
[14]鲁庆尧，王树进. 我国农业面源污染的空间相关性及影响因素研究[J]. 经济问题， 2015，（12）： 93-98.
[15]沈能，王艳. 中国农业增长与污染排放的EKC曲线检验：以农药投入为例[J]. 数理统计与管理， 2016，（4）： 614-622.
[16]吴义根，冯开文，李谷成. 人口增长、结构调整与农业面源污染——基于空间面板STIRPAT模型的实证研究[J]. 农业技术经济. 2017，（3）： 75-87.
[17]颜廷武，田云，张俊飚，等. 中国农业碳排放拐点变动及时空分异研究[J]. 中国人口·资源与环境， 2014，（11）： 1-8.
[18]朱兆良，David Norse，孙波. 中国农业面源污染控制对策[M]. 北京：中国环境科学出版社， 2006.
[19]朱兆良. 农田中氮肥的损失与对策[J]. 生态环境学报， 2000， 9（1）： 1-6.
[20]Ju X T， Xing G X， Chen X P， et al. Reducing Environmental Risk by Improving N Management in Intensive Chinese Agricultural Systems[J]. Proc Natl Acad Sci U S A. 2009， 106（9）： 3041-3046.
[21]Cai， M.， Li， H. E.， Zhuang， Y. T.， & WANG， Q. H. Application of modified export coefficient method in polluting load estimation of non-point source pollution[J]. Journal of Hydraulic Engineering， 2004， 35（7）：0040-0045.
[22]陈敏鹏，陈吉宁，赖斯芸.中国农业和农村污染的清单分析与空间特征识别[J].中国环境科学，2006，6（26）：751-755.
[23]李海鹏， 张俊飚. 中国农业面源污染的区域分异研究[J]. 环境保护， 2009， 30（2）：43-45.
[24]郝芳华，杨胜天，程红光，步青松，郑玲芳.大尺度区域非点源污染负荷计算方法[J].环境科学学报，2006，（3）：375-383.
[25]Kaufmann R K， Davidsdottir B， Garnham S， et al. The determinants of atmospheric SO 2 concentrations： reconsidering the environmental Kuznets curve[J]. Ecological Economics. 1998， 25（2）： 209-220.
[26]孙圣民，陈强. 家庭联产承包责任制与中国农业增长的再考察——来自面板工具变量法的证据[J]. 经济学（季刊）， 2017，（2）： 815-832.
[27]Kelejian H H， Prucha I R. Estimation of simultaneous systems of spatially interrelated cross sectional equations[J]. Journal of Econometrics. 2004， 118（1-2）： 27-50.
[28]Moran P A. Notes on continuous stochastic phenomena.[J]. Biometrika. 1950， 37（1-2）： 17.
（责任编辑 吴晓妹）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 18:27:44