《高中数学数形结合解题技巧》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

高中数学数形结合解题技巧

范文

王获

【摘要】随着教育改革的逐步深入，培养、加强学生的思维思考能力变得十分重要.在学习中利用数学思想解答各类问题越来越受学生喜爱.数形结合思想是高中数学学习过程中十分重要的数学思想之一，借助数形结合思想解题有利于学生理解数学知识点，扩展解题思路与解题技巧，提高分数.因此，本文将从“集合问题”“函数问题”“不等式、方程问题”三个方面展开探讨，浅谈数形结合思想在这几个内容中应用的技巧.

【关键词】高中数学;数形结合思想;解题技巧

一、了解数形结合思想，如何利用

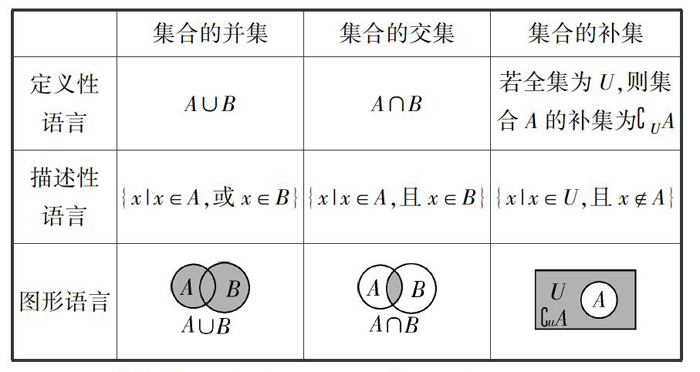
数形结合是一种常见的数学问题解决方法，也是数学研究和学习中的重要思想;在高中，“数”和“形”是我们数学研究的两个基本对象.“数形结合”即是数字与图形结合.

“以形助数”可以将复杂的问题步步简单化、让抽象的问题内容具体化;能够把抽象的数学语言变为直观的图形语言、把抽象的数学思维变为直观的形象思维.“以数助形”有助于把握数学问题的本质，从根本上找到解决问题的方法.

如下图：

二、借助数形结合思想，解答集合问题

集合问题的处理是高中数学教学中十分重要的内容，无论是簡单的数量集合还是复杂的应用题，高中生在解答时都很容易造成答案的错误.所以教师在教学时就可以借助数形结合思想，引入文氏图，让学生在数形结合思想的引导下解答有关几何的问题.

例1 在某地区农户抽样调查中，电冰箱的拥有率是49%，电视机的拥有率是85%，且有44%的农户拥有洗衣机，有63%的农户至少拥有上述三种电器中的两种以上，有25%的农户三种电器都齐全，那么一种电器也没有的贫困户所占的百分比是多少？

解设调查了100户，全集U={被调查的100户农户}，A={100户中拥有电冰箱的农户}，B={100户中拥有电视机的农户}，C={100户中拥有洗衣机的农户}.

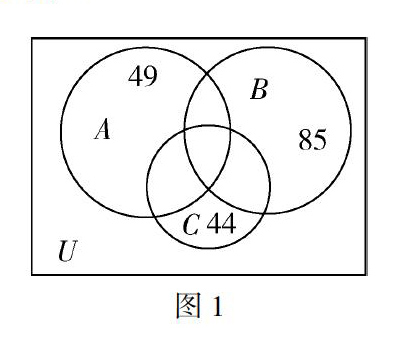
接着，教师可以引导学生根据题目中的已知条件，画出相应的文氏图，如图1.

通过观察可知：三种电器至少拥有一种的农户有49+85+44-63-25=90（户）.

∴一种电器也没有的贫困户所占的百分比是10%.

三、借助数形结合思想，解答函数问题

函数是高中数学教学中的重中之重，学生在解答函数问题的过程中，需要考虑到多方面的因素，尤其是定义域、最值以及零点的内容的求解，需要根据实际情况展开相应的讨论分析，借助数形结合思想，可以全面考虑问题，从而完成问题的解答.在例2、3这类题目的解答过程中，教师需要让学生注重函数图像，仔细观察图像和数据，将形转化为数，从而得出一定的函数关系式，进行有效计算得出题目答案.

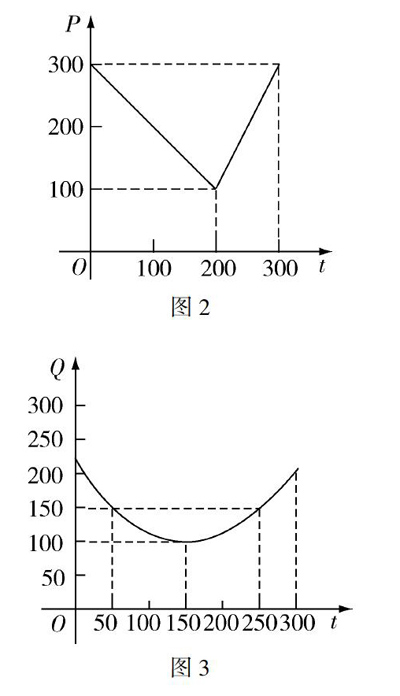
例2 从二月一日起的300天内，图2表示西红柿的市场售价P和上市时间t的关系;图3表示西红柿的种植成本Q和上市时间t的关系.求市场售价和上市时间之间的函数关系式，以及种植成本和时间的函数关系式.

解根据图2，可得市场售价和上市时间的函数关系式P=300-t，0≤t≤200，2t-300，200

根据图3，可得种植成本与上市时间的函数关系式Q=1200（t-150）2+100，0≤t≤300.

例3 函数f（x）=|x-2|-ln x在定义域内的零点的个数为.

解析由题意可知f（x）的定义域为（0，+∞），我们将这个函数拆开看可以得到：

A函数：y1=|x-2|（x>0），

B函数：y2=ln x（x>0），

画出两个函数图像如图4所示，

由图可知函数f（x）在定义域内的零点个数为2.故填2.

数形结合的思想就是在遇到一些难以解决的代数问题时，引入图形来解决，既直观又准确.这样做可以使学生全面考虑题目的各种情况，保证解题的完整性.

四、借助数形结合思想，解答不等式、方程问题

除了集合、函数问题以外，不等式和方程问题也是数学高考常考的热点内容，因此，教师同样要培养学生在不等式、方程问题中的数形结合思想.

在高中数学教学课堂中，开展不等式和方程的教学，十分有利于提高学生在数学方面的思维能力以及数学解题能力.所以，高中数学教师需要让学生在解答数学问题的过程中，巧妙运用数形结合的思想方法，借助图形展示不等式或者方程之间的数量关系，实现问题的有效解答.在例4、5的解题过程中，教师就需要引导学生采取分段函数的方式解不等式，同时，根据分段函数画出相应的图像，使问题能够得到有效解答.

例4 已知函数f（x）=|2x+1|-|x-4|.

（1）解不等式f（x）>2.

（2）求函数y=f（x）的最小值.

解先将函数分成三个部分：x<-12，-12≤x<4，x≥4得f（x）=-x-5x<-12，

3x-3-12≤x<4，

x+5（x≥4），画出图形，如图5所示.

（1）根据图形及解析式，令3x-3=2，解得x=53，令-x-5=2，解得x=-7，所以不等式f（x）>2的解集是xx>53或x<-7

（2）由图5知y=f（x）的最小值是-92.

注：分段时不应遗漏区间的端点值.

例5 若关于x的方程|x|=a-x只有一个解，则实数a的取值范围是.

解析首先引领学生将方程拆开得到：

函数y=|x|与y=a-x，

画出图像，如图6所示.由图像知当a>0时，

方程|x|=a-x只有一个解.

故填（0，+∞）.

总之，在不等式、方程等问题的求解过程中，教师应当引导学生借助相应的图像，分析不等式或者方程的相对应的图形，使得代数问题几何化，从而利用图像实现问题的高效准确解答.

五、结语

综上所述，虽然高中数学知识错综复杂，但是在许多题目中都可运用数形结合的方法.数形结合的解题技巧能够有效拓宽学生解题的思路，提高学生在数学各类问题中的解题能力与解题效率.因此，高中数学教师应当在教学的过程中不断总结和探究，使得学生能够在学习的过程中，灵活运用数形结合思想，真正掌握数形结合的精髓，不断加强思维思考能力.

【参考文献】

[1]谭宁萱.高中数学数形结合的解题技巧[J].高考，2018（26）：213.

[2]杲东.高中数学数形结合解题的技巧[J].数理化学习（高三版），2014（11）：8.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。