《思维导图在大学高等数学教学中的运用》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

思维导图在大学高等数学教学中的运用

范文

施静

【摘要】思维导图作为一种有效的思维模式，引入大学高等数学课程的课堂教学中，不仅能拓展学生的思维，而且能激发学生学习高等数学的兴趣及创造性.

【关键词】思维导图;高等数学课程;教学实践

一、思维导图概述

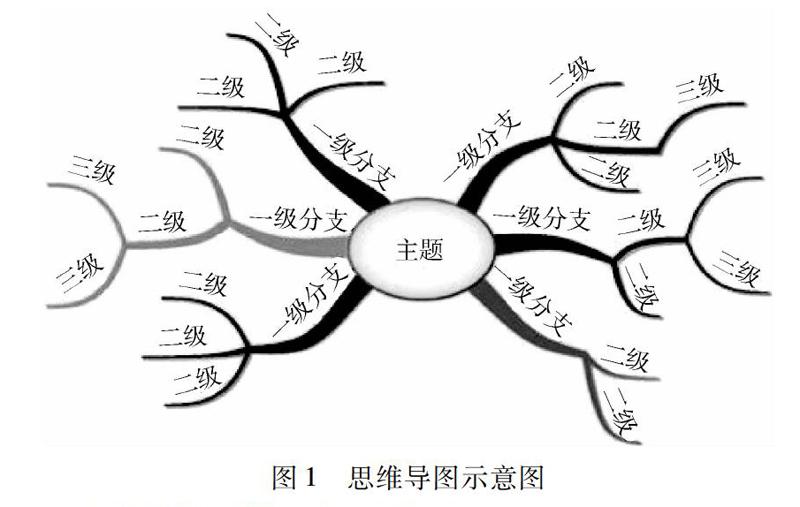
思维导图又称心智地图，是一种图像式思维的工具以及一种利用图像式思考辅助工具（见图1）.思维导图是使用一个中央关键词或想法引起形象化的构造和分类的想法;它用一个中央关键词或想法以辐射线形连接所有的代表字词、想法、任务或其他关联项目的图解方式.

托尼·博赞在《思维导图》一书中表述了思维导图有四个基本特征：

① 注意的焦点清晰地集中在中央图像上.

② 主题作为分支从中央图像向四周放射.

③ 一个关键图像或者印在相关线条上的关键词构成了分支，分支这种形式也可以将比较不重要的话题表现出来，附在较高层次的分支上.

④ 各分支形成一个相互连接的节点结构.[1]

近年来思维导图完整的逻辑架构及全脑思考的方法更被世界和中国广泛应用在学习及工作方面，大量降低所需耗费的时间以及资源.[2]

二、高等数学课程内容的特点

高等数学是一门基础课程，也是各学科的核心课程.它是由微积分学，较深入的代数学、几何学以及他们之间的交叉内容所形成的一门基础学科.

（一）高等数学课程内容庞杂，学生一时难以掌握

《高等数学》分上、下两册.上册以函数的知识作为过渡，以运动和变化的观点引出极限，再以极限研究函数的变化率，形成一元函数微分学;从面积问题引出定积分，并与微积分互为逆运算建立联系，形成微积分的基本定理，构成一元函数积分学.下册通过空间解析几何和向量代数，进一步把一元函数微积分学推广到多元函数微积分学上.

以上内容相互之间有着严密的逻辑性，部分知识点有着高度的抽象性，50 % 的学生面对高数知识点，一时难以掌握.

（二）学生的积极性在传统的授课环境下难以调动

目前，高等数学课程的教学仍然以灌输式的教学为主，缺乏引导为主，自主学习的教学理念，学生在高数知识的学习过程中长期得不到系统的引导和启发，失去了对高等数学学习的兴趣，学生学习高数的积极性受到很大程度的抑制，全面影响了学生的自主创新和个性发展.

三、思维导图模式在高等数学课程教学中的应用

（一）将思维导图引入高等数学课程课前预习中

在以往的高等数学授课期间，学生很少进行课程预习.究其原因，是学生的预习漫无目的，抓不住重点和难点.

笔者认为，思维导图就是激发学生学习建筑构造的兴趣，课前预习的思维导图课前事先发给每名学生，利用思维导图进行预习.根据调研，课前预习的同学很少，而在利用思维导图进行预习以后，预习的同学变得越来越多.

制作课前预习思维导图的步骤如下：

（1）根据下次讲课内容，列出关键词;

（2）将这些关键词按照一定的逻辑顺序列出来;

（3）将重点和难点做好标识.

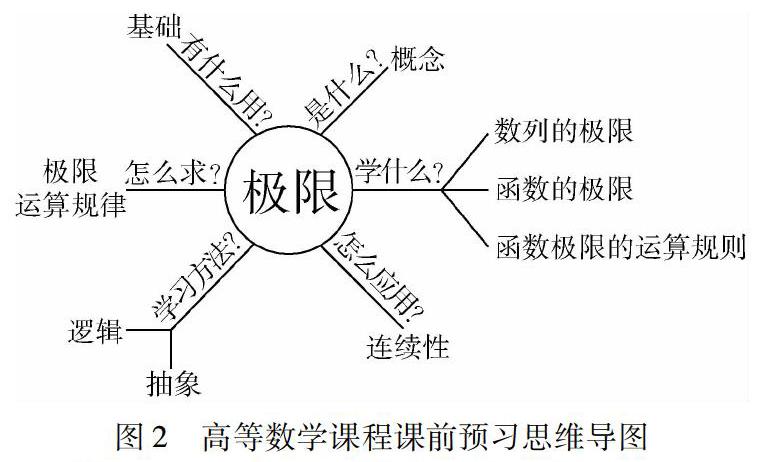
建筑构造课程课前预习思维导图如图2所示.

（二）将思维導图嵌入高等数学课堂教学

思维导图非常适合课堂教学.笔者以高等数学第一章函数与极限中的极限为例，介绍一下思维导图在课堂教学中的应用.极限是高等数学中的重要的基础概念，几乎所有连续、微分、积分的基本概念都是建立在极限概念的基础之上的.学生必须将极限这一概念弄懂学透，才能在将来的高数学习中游刃有余.在课堂讲授过程中，按照高等数学的教学大纲要求，学生必须掌握极限的概念.本次课教学的关键点、重点与难点为：

（1）关键点为在数列极限中如何找到N以及在函数极限中如何找到δ;

（2）重点为极限的性质;

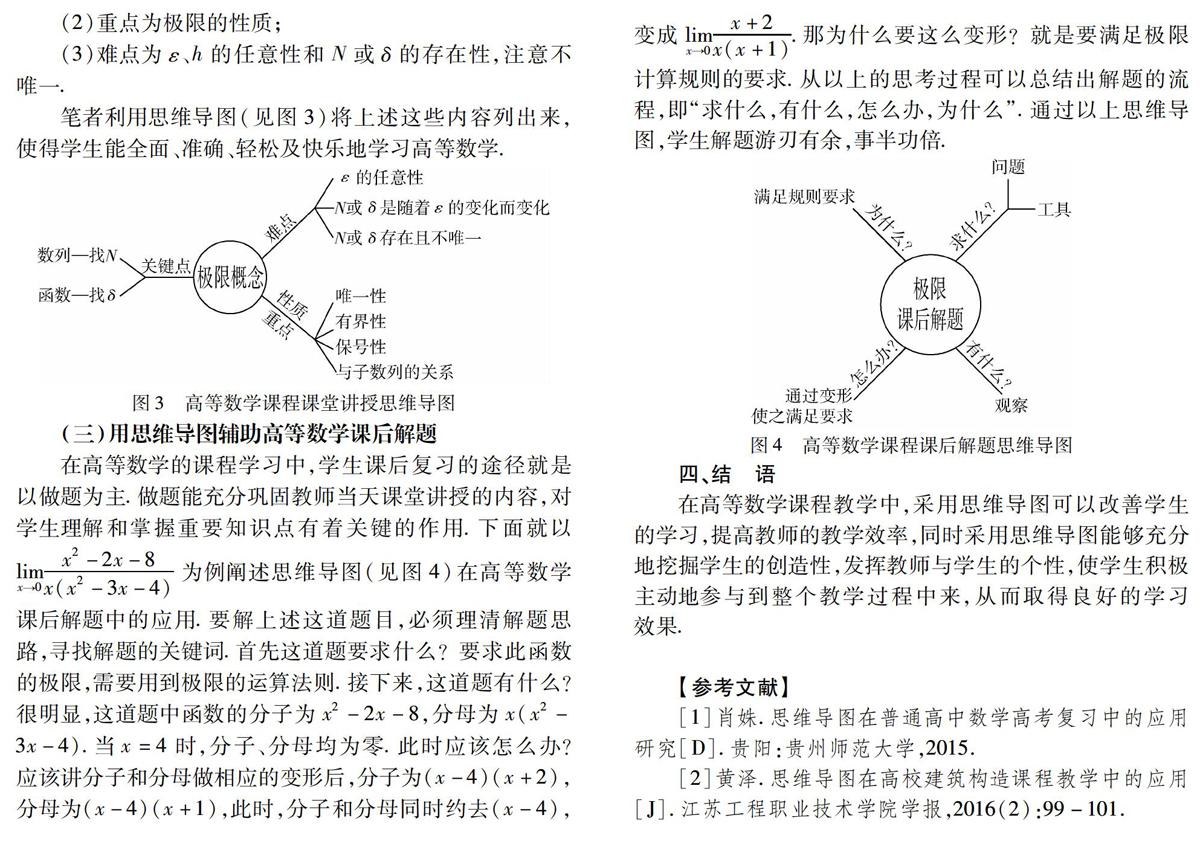
（3）难点为ε、h的任意性和N或δ的存在性，注意不唯一.

笔者利用思维导图（见图3）将上述这些内容列出来，使得学生能全面、准确、轻松及快乐地学习高等数学.

（三）用思维导图辅助高等数学课后解题

在高等数学的课程学习中，学生课后复习的途径就是以做题为主.做题能充分巩固教师当天课堂讲授的内容，对学生理解和掌握重要知识点有着关键的作用.下面就以 lim x→0? x2-2x-8 x（x2-3x-4） ?为例阐述思维导图（见图4）在高等数学课后解题中的应用.要解上述这道题目，必须理清解题思路，寻找解题的关键词.首先这道题要求什么？要求此函数的极限，需要用到极限的运算法则.接下来，这道题有什么？很明显，这道题中函数的分子为x2-2x-8，分母为x（x2-3x-4）.当x=4时，分子、分母均为零.此时应该怎么办？应该讲分子和分母做相应的变形后，分子为（x-4）（x+2），分母为（x-4）（x+1），此时，分子和分母同时约去（x-4），变成 lim x→0? x+2 x（x+1） .那为什么要这么变形？就是要满足极限计算规则的要求.从以上的思考过程可以总结出解题的流程，即“求什么，有什么，怎么办，为什么”.通过以上思维导图，学生解题游刃有余，事半功倍.

四、结语

在高等数学课程教学中，采用思维导图可以改善学生的学习，提高教师的教学效率，同时采用思维导图能够充分地挖掘学生的创造性，发挥教师与学生的个性，使学生积极主动地参与到整个教学过程中来，从而取得良好的学习效果.

【参考文献】

[1]肖姝.思维导图在普通高中数学高考复习中的应用研究[D].贵阳：贵州师范大学，2015.

[2]黄泽.思维导图在高校建筑构造课程教学中的应用[J].江苏工程职业技术学院学报，2016（2）：99-101.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。