《基于Heaviside过滤的多相材料拓扑优化设计》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

基于Heaviside过滤的多相材料拓扑优化设计

范文

曹浩　彭罗

摘要：为解决以柔顺度最小化为目标的多相材料结构拓扑优化问题，提出了一种新的拓扑优化求解方法。首先，基于RAMP方法和Heaviside过滤函数形成设计变量和物理变量，构建以柔顺度为目标的多相材料结构拓扑优化模型及近似优化模型;然后，采用荣见华等提出的改进交替主动相算法，最后，采用MMA求解器优化求解。给出的算例结果表明，与现有方法相比，该方法可以得到更优的拓扑解，并解决多相材料结构单元几种材料并存的问题。

关键词：Heaviside过滤;交替主动相;MMA求解

中图分类号：TB34文献标识码：A文章编号：1003-5168（2020）13-0055-03

Topological Optimization Design of Multiphase

Materials Based on Heaviside Filtering

CAO Hao PENG Luo

（School of Automotive and Mechanical Engineering， Changsha University of Science and Technology，Changsha Hunan 410076）

Abstract： In order to solve the topology optimization problem of multiphase material structure with the objective of minimizing the flexibility， a new topology optimization method was proposed. Firstly， based on the RAMP method and the Heaviside filter function， the design variables and physical variables were formed， and the topological optimization model and the approximate optimization model of the multiphase material structure with the flexibility as the goal were constructed. Then， the improved alternating active phase algorithm proposed by Rong Jianhua and others was used， and finally， the MMA solver was used to optimize the solution. The results show that compared with the existing method， this method can get better topological solution and solve the problem that there are several materials coexisting in the multiphase material structure element.

Keywords： Heaviside filtering;alternating active phases;MMA solution

1 研究背景

在解決多相材料结构单元几种材料并存的问题时仍存在一定的难度。在单相材料拓扑优化中，为减少结构拓扑中存在的一些中间密度单元或灰度单元，Guest等首先提出了采用Heaviside函数进行过滤的方法[1]。之后，Sigmund在改进的Heaviside密度过滤方法基础上提出了基于形态学的过滤方法，该类方法都能获得0/1分布较为清晰的优化结果[2]。Sigmund采用密度过滤和Heaviside密度映射对柔性机构进行优化，获得了清晰的结构拓扑[3]。Cui等提出用Heaviside阈值函数解决多相材料结构单元有几种材料并存的问题[4]。在设计变量变化较大时，结构的性能指标出现较大跳跃，导致出现求解振荡问题。

2 多相材料插值模型

为了获得清晰的结构拓扑优化解，采用Guest等[5]提出的光滑Heaviside函数，将单元设计变量[ρsi]形成物理变量场[ρsi]，使用物理变量[ρsi]进行结构有限元分析。

根据Zhou等[6]提出的RAMP材料插值模型，提出改进的RAMP材料插值模型，构建单元刚度矩阵的表示式：

式中，[v]为经验参数，取值为6;[Ki]表示当[m]相实体材料的物理变量为[ρsi]时第[i]号单元的刚度阵;[K0i]表示单元的弹性模量为1.0时第[i]号单元的刚度阵;[Emin]表示一个极小的值。

结构中任意的设计单元有

本文以结构柔顺度最小化为目标，实体材料体积为约束的多相材料结构拓扑优化模型近似表示为式（4）：

式中，[Cρ]表示结构柔顺度;[V（0）]表示初始设计的结构体积;[Vk+1s]表示第[k+1]步第[s]相材料的体积限，计算公式为：

式中，[γ1]取0.01（本文中所有算例）;[Vk+1s]相对于外循环迭代步数[k]是单调变化的，从而确保有限迭代步后，[β]为曲率参数[β]变化后的第一迭代步的迭代步编号的集合;[V（k）]表示第[k]迭代步设计的结构体积。

3 目标函数和体积的灵敏度分析

结构的任意性能函数[f（ρ）]对设计变量[ρsi]的导数可表示为：

目标函数结构柔顺度对设计变量[ρsi]的一阶导数为：

对于任意相实体材料体积对设计变量[ρsi]的一阶导数表示式：

4 改进的交替主动相算法及求解优化

Tavakoli等[7]提出交替主动相方法解决多相材料的求解问题，之后俞燎宏等[8]改进交替主动相算法。本文引用俞燎宏等人的交替主动相算法进行优化求解，用[a]和[b]分别表示这两相主动相材料[[a=1，2，…，m];[b=a+i（i=1，2，…，m-a）]]，则将式（3）转化为：

设[yq=x（a-1）×N+i]，将[ρai=x（a-1）×N+i]作为主动设计变量，[ρbi=x（b-1）×N+i]作为从动设计变量，其他变量不变。从动设计变量可以看作是主动设计变量的函数，由式（10）得：

将优化模型式（4）的求解转化为式（13）二元相拓扑优化子模型的求解。

最后可采用MMA算法对子模型式（13）进行求解，然后，循环此过程，直到[r=m（m-1）/2]。取[ρsi=x（k+1），m（m-1）/2（s-1）×N+i]更新设计变量，完成一次内迭代循环。

5 优化算例

采用本文提出的Heaviside函数拓扑优化方法解决多相材料结构单元有几种材料并存的问题，设计域如图1所示。边界条件为：左边固定约束，右边下端点作用一个垂直向下的载荷[F=1]，泊松比[ν]=0.3。初始设计域被离散成4 608（长[L]=96个，宽[H]=48个）个四节点平面单元，过滤半径[rmin=3.0?]（[?]是结构单元边长的最小尺寸）。

假设结构由2相实体材料和1相空洞材料组成。第1相和第2相实体材料的弹性模量分别为1和2，第3相材料（空洞材料）的弹性模量设为[1.0e-9]。第1相和第2相实体材料目标体积比分别预定为15%和25%。此算例中，体积指数[αv]取1.025，体积约束限参数[γ1]取0.01，收敛参数取[ε1=0.01]。

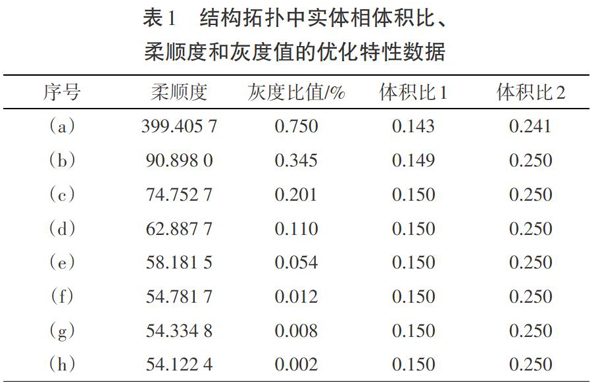
表1给出了实体相体积比、柔顺度和灰度值的优化特性数据，由表1中灰度比值可知，构型黑白比转化为0.002，已经达到了0/1分布的要求，拓扑构型清晰度已经非常清晰了。图2给出了柔顺度和实体相体积的优化历程曲线。

优化历程曲线

图3是分别采用本文方法和Tavakoli R等人提出的[7]方法求解优化问题时获得的局部最优结构拓扑图以及其最小柔顺度值。从图3可知，由本文方法优化得到的最后的拓扑构型，实体相构型边缘呈锯齿状，表明已得到非常清晰的拓扑构型。

6 结论

本文针对多相材料拓扑优化问题，提出了一种新的解决多相材料结构单元几种材料并存的问题的结构拓扑优化求解方法。通过本章理论推导和数值算例验证，确定了本文方法的可行性。本文提出一个新的灵敏度过滤Heaviside函数，引入改进的RAMP插值函数使得拓扑结构能稳定收敛到最优解。采用本文方法分别对三相材料进行拓扑优化，对比现有文献方法，得到更优的拓扑优化解。本文方法很好地解决了多相材料拓扑构型不清晰的问题，并获得较好的结构拓扑。

参考文献：

[1]Guest J K ， J. H. Prévost， Belytschko T . Achieving minimum length scale in topology optimization using nodal design variable and projection functions[J].International Journal for Numerical Methods in Engineering，2004（2）：238-254.

[2]Schevenels M， Sigmund O. On the implementation and effectiveness of morphological close-open and open-close filters for topology optimization[J]. Structural and Multidisciplinary Optimization， 2016（1）：15-21.

[3]Sigmund O . Morphology-based black and white filters for topology optimization[J]. Structural and Multidiplinary Optimization，2007（4-5）：401-424.

[4]Mingtao Cui，Yifei Zhang，Xinfeng Yang，et al. Multi-material proportional topology optimization based on the modified interpolation scheme[J]. Engineering With Computers，2018（34）：287-305.

[5]王健，程耿東.多工况应力约束下连续体结构拓扑优化设计[J].机械强度，2003（1）：55-57，75.

[6]Zhou S，Wang M Y. Multimaterial Structural Topology Optimization with a Generalized Cahn-Hilliard Model of Multiphase Transition[J]. Structural and Multidisciplinary Optimization，2007（2）：89-111.

[7]Tavakoli R，Mohseni S M . Alternating active-phase algorithm for multimaterial topology optimization problems： A 115-line MATLAB implementation[J]. Structural & Multidisciplinary Optimization，2014（4）：621-642.

[8]俞燎宏，荣见华，唐承铁，等.基于可行域调整的多相材料结构拓扑优化设计[J].航空学报，2018（9）：117-133.

收稿日期：2020-04-08

基金项目：国家自然科学基金（11772070，11372055）;中国建筑第五工程局有限公司科研项目。

作者简介：曹浩（1994—），男，硕士，研究方向：结构拓扑优化设计;彭罗（1995—），男，硕士，研究方向：结构拓扑优化设计。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。