物理程序性知识教学探索
胡慧青
1 问题提出的意义
现代知识观根据反映活动的形式不同,将知识分为陈述性知识和程序性知识.程序性知识也叫操作性知识,是个体难以清楚陈述、只能借助于某种作业形式间接推测其存在的知识.这类知识主要用来回答“怎么想”“怎么做”的问题.
获得程序性知识的过程体现了知识学习的连续性和完整性,也体现了能力的养成途径,因此,对于克服传统教学中技能与知识相脱节的形式主义倾向及发展学生的能力有很重要的理论与实践意义.
2 典型案例
基于高中学生的特点,下面以《牛顿第二定律》的教学为例,采用科学探究和变式练习教学对物理学科中的程序性知识的教学进行探索.
首先明确任务是科学探究a与F、m的定量关系.由于任务比较复杂,学生没有头绪,所以我们采用“小步子”教学引导学生将任务分为三步来探究.
第一步,大胆实验,自主探究.学生根据控制变量法设计初步实验方案如图1.小车作为研究对象,通过在小车上增减砝码改变小车质量,小车受到的拉力大致是钩码的重力,通过增减钩码来改变小车受到的拉力.学生观察小车的运动,研究小车的加速度a与拉力F及小车质量m的关系.

第二步,改进装置,定量求证.因为初步实验中没有测量a,所以无法定量a与F、m的关系.针对实验中的问题,我们引导学生将课堂进一步推进,根据s=at2/2可知在t相同时,a1/a2=s1/s2,将比较难测量的加速度转换为位移的测量,然后确定新的实验方案,改进实验装置如图2.该方案操作简单,不必测量时间,形象直观,学生也能自主地处理数据,比较准确地得到结论,大大地激发了学生的兴趣.
第三步,趁热打铁,逐层深入.充分发挥教师的主导作用,设置了几个具有思维梯度的问题让学生讨论,层层递进,以达成教学目标.问题1:力的单位“牛顿”的意义是什么?问题2:牛顿第二定律更一般的表述是什么?问题3:定律中的力是指什么力?问题4:加速度到底取决于什么?如何认识a=Δv/Δt与a=F/m?
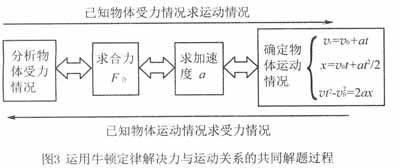
在得到结论之后,通过变式练习,应用定律来解决生活生产中的实际问题.我们选择“汽车是否超速追尾”问题为例,首先引导学生明确已知量、待求量,寻找各量之间的关系,代入求解,解决实际问题,然后,总结“解决已知力求运动”的共同解题过程如图3.接着以“吊车对缆绳的要求”作为学生的巩固练习,提炼“解决已知运动求力”的共同解题过程如图3.最后,实践操作——学生自制加速度计,学生设计加速度计的原理图、制作加速度计并检测小车运动的加速度.
3 几点体会
3.1 陈述性知识和程序性知识的学习是互为条件、互相促进和相互转化的
牛顿第二定律的内容是陈述性知识,当学生能够复述出定律时,表明学生已经完成了陈述性知识的学习.但是,不能被学生用言语陈述的表象所蒙蔽,更不能以言语陈述为最终教学目的,应促进学生相应技能的形成与发展.所以,在教学中我们应该创设问题情境,以如何获得新的陈述性知识来设计教学策略,给学生充分的时间和机会去探究、去理解、去讨论,将静态的陈述性知识由动态的程序性知识获得.接着,教师提供适当的变式练习,让学生又将静态的知识转化为动态的技能,掌握程序性知识学习的高级阶段——解决实际问题.
总之,陈述性知识的获得常常是学习程序性知识的基础,程序性知识的获得又为获取新的陈述性知识提供了可靠保证.
3.2 科学探究是获得程序性知识的一种非常有效的方法
如果学生只是记住了物理概念和定律的内容,至于结论怎么来的、探究的过程和方法是什么都没有体验、没有思考,那么只能说明学生对概念和规则的学习还处于陈述性阶段,尚未转化为能力和技能.
课程标准要求学生“理解牛顿运动定律.”至于如何让学生理解,与此相关的程序性知识还需要教师自己总结开发.科学探究和物理实验是获得程序性知识的一种有效方法.新问题进入原有的命题网络,与原有知识形成联系,学生通过探究、实验习得学习的过程和方法,将原有的知识进一步推进,建立一种新的陈述性知识.学生在此过程中获得程序性知识,提高能力,发展技能.学生在已经具备牛顿第一定律与惯性概念的基础上,通过探究加速度与力、质量的定量关系,得到牛顿第二定律.实验过程中,学生在实际的学习情景中解决具体的物理问题,设计实验方案、改进装置、实验操作、记录数据、总结结论等等,学生不仅牢固地掌握了知识,更重要的是思维能力的批判性、逻辑性、创造性都得到了充分的发展,有利于创造性人才的培养.
3.3 变式练习是程序性学习非常关键的一步
我们经常看到一些学生对一些公式、定义、定律说得头头是道,但一旦遇到问题就束手无策了,这种情况的原因往往是缺乏练习的结果.这时学生所掌握的概念和规则主要以一种静态的方式存储,要使这种静态的“陈述性知识”转化为动态的“技能”,则需要通过适当的变式练习来完成,将命题网络方式存储的知识转化为以“产生式”为表征的程序性知识.
解答物理练习的最初阶段,适宜选择与原先学习情景相似的问题情景进行练习,随着知识逐渐稳定和巩固,问题类型要有变化,可以逐渐演变为与原先学习情景完全不同的新情景,以促进学生习得的概念和规则的纵向迁移.
利用F=ma求解实际问题,如果没有真正理解其物理思想和方法,当遇到新的物理情景时,就觉得“无从下手”或者“丢三纳四”.怎样才能让学生不是机械化的模仿和简单记住解题步骤,而是真正做到“知其然,还知其所以然”呢?通过变式练习可以达到这样的目的.应用F=ma求解的变式练习如下:
例题 通过“汽车刹车”问题,初步体会F=ma中的F是合力,以及定律的矢量性.并提炼“已知力求运动”的解题思路.(图4)
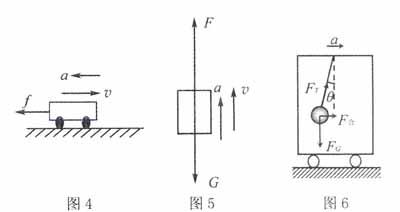
变式1 “吊车对缆绳的拉力要求”,将水平运动变为竖直运动,将一个力变为两个力.并提炼“已知运动求力”的解题思路.(图5)
变式2 设计“加速度计”的原理图,进一步将两力共线变为不共线求合力.提高解题的难度.(图6)
通过教师提供适当的变式练习,让学生熟知规则适用的各种不同情景,并能在情景中,通过新旧知识的融会贯通,由浅入深、循序渐进地分析问题,并且通过串接和回顾,将产生式的条件与问题解决相联系.这样,不仅可以丰富学生的认知结构,还可以培养学生分析能力和正确寻找解题思路的能力,才真正有可能在以后碰到不同的情景时,一旦识别了产生式中的条件,就有可能迅速地作出相应的行动反应,从而正确解决所面临的问题,实现触类旁通.
由此可见,教师只有在教学中精心设计,才有可能避免将程序性知识当作陈述性知识来教,满足于单纯的记忆要求,也才有可能避免大量的重复练习.科学探究和变式练习有效地促进了学生程序性知识的学习,提高学生解决问题的能力,培养学生创新意识和创新能力,将知识学习与能力培养紧密、和谐地结合起来.
总之,突破传统知识观念的束缚,理解和深化现代认知心理学关于知识分类的理论,探讨程序性知识的传授与学习,对于解决长期困扰我们的知识与能力的错位,以及如何在知识学习中发展能力的问题,将是一个实际的解决措施,有利于真正把素质教育落到实处.
1 问题提出的意义
现代知识观根据反映活动的形式不同,将知识分为陈述性知识和程序性知识.程序性知识也叫操作性知识,是个体难以清楚陈述、只能借助于某种作业形式间接推测其存在的知识.这类知识主要用来回答“怎么想”“怎么做”的问题.
获得程序性知识的过程体现了知识学习的连续性和完整性,也体现了能力的养成途径,因此,对于克服传统教学中技能与知识相脱节的形式主义倾向及发展学生的能力有很重要的理论与实践意义.
2 典型案例
基于高中学生的特点,下面以《牛顿第二定律》的教学为例,采用科学探究和变式练习教学对物理学科中的程序性知识的教学进行探索.
首先明确任务是科学探究a与F、m的定量关系.由于任务比较复杂,学生没有头绪,所以我们采用“小步子”教学引导学生将任务分为三步来探究.
第一步,大胆实验,自主探究.学生根据控制变量法设计初步实验方案如图1.小车作为研究对象,通过在小车上增减砝码改变小车质量,小车受到的拉力大致是钩码的重力,通过增减钩码来改变小车受到的拉力.学生观察小车的运动,研究小车的加速度a与拉力F及小车质量m的关系.

第二步,改进装置,定量求证.因为初步实验中没有测量a,所以无法定量a与F、m的关系.针对实验中的问题,我们引导学生将课堂进一步推进,根据s=at2/2可知在t相同时,a1/a2=s1/s2,将比较难测量的加速度转换为位移的测量,然后确定新的实验方案,改进实验装置如图2.该方案操作简单,不必测量时间,形象直观,学生也能自主地处理数据,比较准确地得到结论,大大地激发了学生的兴趣.
第三步,趁热打铁,逐层深入.充分发挥教师的主导作用,设置了几个具有思维梯度的问题让学生讨论,层层递进,以达成教学目标.问题1:力的单位“牛顿”的意义是什么?问题2:牛顿第二定律更一般的表述是什么?问题3:定律中的力是指什么力?问题4:加速度到底取决于什么?如何认识a=Δv/Δt与a=F/m?
在得到结论之后,通过变式练习,应用定律来解决生活生产中的实际问题.我们选择“汽车是否超速追尾”问题为例,首先引导学生明确已知量、待求量,寻找各量之间的关系,代入求解,解决实际问题,然后,总结“解决已知力求运动”的共同解题过程如图3.接着以“吊车对缆绳的要求”作为学生的巩固练习,提炼“解决已知运动求力”的共同解题过程如图3.最后,实践操作——学生自制加速度计,学生设计加速度计的原理图、制作加速度计并检测小车运动的加速度.

3 几点体会
3.1 陈述性知识和程序性知识的学习是互为条件、互相促进和相互转化的
牛顿第二定律的内容是陈述性知识,当学生能够复述出定律时,表明学生已经完成了陈述性知识的学习.但是,不能被学生用言语陈述的表象所蒙蔽,更不能以言语陈述为最终教学目的,应促进学生相应技能的形成与发展.所以,在教学中我们应该创设问题情境,以如何获得新的陈述性知识来设计教学策略,给学生充分的时间和机会去探究、去理解、去讨论,将静态的陈述性知识由动态的程序性知识获得.接着,教师提供适当的变式练习,让学生又将静态的知识转化为动态的技能,掌握程序性知识学习的高级阶段——解决实际问题.
总之,陈述性知识的获得常常是学习程序性知识的基础,程序性知识的获得又为获取新的陈述性知识提供了可靠保证.
3.2 科学探究是获得程序性知识的一种非常有效的方法
如果学生只是记住了物理概念和定律的内容,至于结论怎么来的、探究的过程和方法是什么都没有体验、没有思考,那么只能说明学生对概念和规则的学习还处于陈述性阶段,尚未转化为能力和技能.
课程标准要求学生“理解牛顿运动定律.”至于如何让学生理解,与此相关的程序性知识还需要教师自己总结开发.科学探究和物理实验是获得程序性知识的一种有效方法.新问题进入原有的命题网络,与原有知识形成联系,学生通过探究、实验习得学习的过程和方法,将原有的知识进一步推进,建立一种新的陈述性知识.学生在此过程中获得程序性知识,提高能力,发展技能.学生在已经具备牛顿第一定律与惯性概念的基础上,通过探究加速度与力、质量的定量关系,得到牛顿第二定律.实验过程中,学生在实际的学习情景中解决具体的物理问题,设计实验方案、改进装置、实验操作、记录数据、总结结论等等,学生不仅牢固地掌握了知识,更重要的是思维能力的批判性、逻辑性、创造性都得到了充分的发展,有利于创造性人才的培养.
3.3 变式练习是程序性学习非常关键的一步
我们经常看到一些学生对一些公式、定义、定律说得头头是道,但一旦遇到问题就束手无策了,这种情况的原因往往是缺乏练习的结果.这时学生所掌握的概念和规则主要以一种静态的方式存储,要使这种静态的“陈述性知识”转化为动态的“技能”,则需要通过适当的变式练习来完成,将命题网络方式存储的知识转化为以“产生式”为表征的程序性知识.
解答物理练习的最初阶段,适宜选择与原先学习情景相似的问题情景进行练习,随着知识逐渐稳定和巩固,问题类型要有变化,可以逐渐演变为与原先学习情景完全不同的新情景,以促进学生习得的概念和规则的纵向迁移.
利用F=ma求解实际问题,如果没有真正理解其物理思想和方法,当遇到新的物理情景时,就觉得“无从下手”或者“丢三纳四”.怎样才能让学生不是机械化的模仿和简单记住解题步骤,而是真正做到“知其然,还知其所以然”呢?通过变式练习可以达到这样的目的.应用F=ma求解的变式练习如下:
例题 通过“汽车刹车”问题,初步体会F=ma中的F是合力,以及定律的矢量性.并提炼“已知力求运动”的解题思路.(图4)

变式1 “吊车对缆绳的拉力要求”,将水平运动变为竖直运动,将一个力变为两个力.并提炼“已知运动求力”的解题思路.(图5)
变式2 设计“加速度计”的原理图,进一步将两力共线变为不共线求合力.提高解题的难度.(图6)
通过教师提供适当的变式练习,让学生熟知规则适用的各种不同情景,并能在情景中,通过新旧知识的融会贯通,由浅入深、循序渐进地分析问题,并且通过串接和回顾,将产生式的条件与问题解决相联系.这样,不仅可以丰富学生的认知结构,还可以培养学生分析能力和正确寻找解题思路的能力,才真正有可能在以后碰到不同的情景时,一旦识别了产生式中的条件,就有可能迅速地作出相应的行动反应,从而正确解决所面临的问题,实现触类旁通.
由此可见,教师只有在教学中精心设计,才有可能避免将程序性知识当作陈述性知识来教,满足于单纯的记忆要求,也才有可能避免大量的重复练习.科学探究和变式练习有效地促进了学生程序性知识的学习,提高学生解决问题的能力,培养学生创新意识和创新能力,将知识学习与能力培养紧密、和谐地结合起来.
总之,突破传统知识观念的束缚,理解和深化现代认知心理学关于知识分类的理论,探讨程序性知识的传授与学习,对于解决长期困扰我们的知识与能力的错位,以及如何在知识学习中发展能力的问题,将是一个实际的解决措施,有利于真正把素质教育落到实处.

