初中数学教学中培养学生动手探索的能力
[摘要]初中数学教学中教师应注重培养学生动手探索的能力.教学中教师可充分利用已有资源,增加学生动手次数与机会,让学生在探索活动中学习数学;自制或改进教具设计方案,體现教具的科学性,尽可能地让学生也能制作相应的学具,进一步加强教学实效;精心设计习题,在习题教学过程中也适当增加能动手实践的环节;组织好数学课外活动,尽可能整合多学科知识.[关键词]动手;探索;数学活动;初中数学
[中图分类号]G633.6? [文献标识码]A? [文章编号]1674-6058(2020)02-0030-02
数学是人类文明的一部分,应用于各个学科,渗透到文明的各个领域,它对人类文化的影响巨大,无论自然科学,还是社会科学.大多数人对数学的印象就是用纸、笔进行运算与证明,不需要实验.其实,“观察、实验、发现、猜想、验证”等的实践活动,数学不比任何其他学科少.实验、试错、建模已经是数学应用中最常见的策略和手段.学生的发展是数学教育的着眼点,学数学不应只重结论,而且不重过程.因此,教师应尽可能在课堂教学中创造机会让学生经历观察、实验、猜想、证明等数学活动过程.
一、激发学习兴趣,多为学生创造动手探索的机会
人的创新精神和实践能力主要依赖于人的智慧、情感和态度,而这些又深深地嵌入实践之中.现在有很多学生认为学习数学枯燥无味,没有学习的兴趣,尤其是当教师为了保证平均分和升学率只知一味地让学生做题、练题时,更使得学生反感学习数学,不利于培养学生的智慧、情感和态度.学生天性喜欢动手探索,教学中不是学生不爱动手,而是很多时候教师没有为学生创造动手探索的机会.因此,教师在数学课堂上应尽可能多地创造机会让学生动手实践,在实践中学习,体验活动过程,积累实践经验,积累与人合作的经验.
二、充分利用已有资源,突破增加动手次数
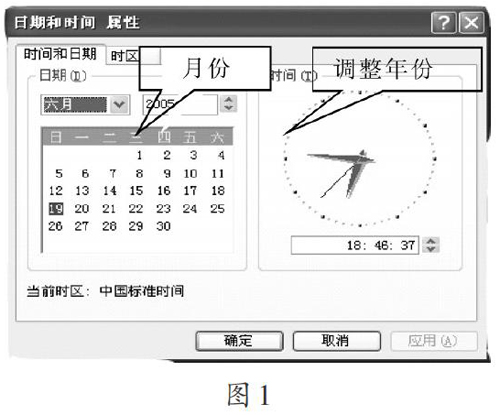
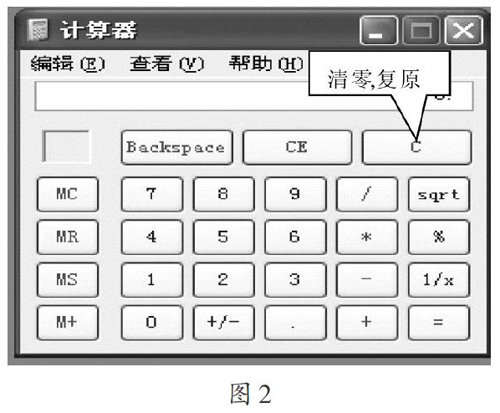
[案例1]北师大版数学七年级上册第三章《字母表示数》第六节《探索规律》教学中,需要学生准备一些日历进行简单的规律探索,在教学过程中发现让学生带日历不能达到人手一本,很有限而且不能实现多次使用.经过考虑,由于信息技术课的开展,现在学生大多都掌握了电脑的基本操作,因此完全可以利用电脑上的万年历(如图1),这样不但给学生提供了大量的、可多次使用的日历进行探索规律的学习,而且每一个学生都可以用不同的原始资料得到相同的结论,体现了他们所总结的规律的一般性.同时在这一教学活动中的计算还可以用电脑上的计算器(如图2)进行,摆脱烦琐的计算,进行有实效的科学探索.
二、自制或改进教具设计方案,体现教具的科学性,加强教学实效
[案例2]探究正方体截面的方法,据我了解一般有两种方法:一是利用多媒体课件展示(例如Z+Z超级画板制作的课件);二是切土豆块.(学生先用土豆制作一些正方体,然后用小刀去“截”正方体,然后观察正方体的截面形状.)第一种方法体现了动态过程,但学生没有动手的经验而且需要一定的空间想象能力;第二种方法学生有动手操作的经历,理论构建在实践的基础上,但学生存在着个体差异,教学中发现大多数学生能找到三角形、四边形的截面,但找不到五边形和六边形的截面.对此,教师可用玻璃裁五块等大的正方形和一块小三角形用玻璃胶粘成一个有开口的正方体玻璃容器.操作简单易行,只需往正方体容器中逐渐注水同时不断地旋转观察即可.利用这一教具既可体现探究的动态过程,又可让学生动手操作,积累数学活动的经验.
三、精心设计习题,在习题教学中适当增加能动手实践的环节
[案例3](2002年山西中考)如图4,有一破残的轮片,现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计两种方案,确定这个圆形零件的半径.
教学中解答这道题的方法有两种,都是纯数学的解法.
一是作图法,利用过三点作圆和垂径定理(如图5),在残片弧上任取三点A、B、C,连接从AB、BC(或AC),分别作AB、BC(或AC)的垂直平分线,两线交于点O,则点O即为圆的圆心,线段OA即为圆的半径.
二是测算法,测量弦AB与弓形高DE的长(如图6),利用相交弦定理,设半径为x,得:
解出x值即为圆的半径,相应可画出与原轮片同样大小的圆.
或运用垂径定理,设半径为r,得:
解方程求出r即可.
实际上,如果我们再进一步思考,可以发现适当改变一下例题的条件不但能和实际生产生活相联系,而且可以培养学生的动手能力.生活中若遇到上述情况怎么办?不用纸笔计算,能否简捷地解决问题呢?
教学中提出上述问题,学生结合上面的两种理论解法,经过多次尝试改进之后制作出了如下两个工具.
工具1:如图7,木条AB与CD互相垂直,且木条CD边所在的直线经过木条AB的中点.根据垂径定理只要使得A、B两点落在圆上,则圆心必在CD所在的直线上.使用工具分别作出圆形工件的任意两条直径,两直径的交点就是圆心.
工具1会受尺寸限制,再改进一下.
工具2:如图8将木条CD钉在木条AB的上面,做成类似丁字尺的工具,由圆的切线的性质可知,将AB放置成与弧相切的位置使得点C为切点.由于CD⊥AB,所以圆心必在CD所在的直线上.同上,两条直径所在的直线的交点就是圆心.
有学生提出,如果残缺的轮片材料是纸,那么对折即可.
圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.反过来,圆的每一条对称轴都过圆心.因此我们只需在不同的两个位置对折破残轮片(如图9),折痕就是对称轴,两条折痕所在直线即两条直径所在直线的交点即圆心.这个办法简单易行,学生当场就能动手验证.
如果我们除了一支笔外什么工具都没有,并且这个破残轮片也不是纸质的,是铁的、钢的或其他硬质材料制作成的,怎么解决?
圆绕圆心旋转任意一个角度,都能够与原来的图形重合.如图10,我们可以先把边缘描下来,沿破残轮片的边缘旋转直至恢复.
四、组织好数学课外活动,尽可能整合多学科知识
[案例4]以制作学生日常生活中常见的包装盒为载体,集成长方体的表面展开图的知识、美术知识(图案、美术字、颜色、视觉效果)、语言知识(文字设计、广告语言、汉语拼音或英语词组)、生产常识(尺寸、材料、商标、生产成本)等,通过小组合作来制作长方体形状的包装盒,可使学生各方面的能力都得到相应的提高.经过观察讨论、设计制作方案、做出作品,最后再考查作品的正确性、形状尺寸是否合理、用料是否节省、外观设计是否美观等一系列活动过程,不但可以让学生学到知识,而且还可以让学生经历数学活动的过程,在活动过程中培养与人合作的情感与能力.
[参考文献]
[1]叶尧城,向鹤梅.全日制义务教育数学课程标准教师读本[M].武汉:华中师范大学出版社,2002.
[2]党永涛.复原残片(初三)[J].数理天地(初中版),2003(7):17.

