剪中心对称图形的两种设计方法之比较
杨建花

摘? 要 中心对称图形是初中数学中非常重要的教学内容,有两种方法可以设计剪中心对称图形,对这两种设计方法进行分析,希望能够提高教学质量。
关键词 初中数学;中心对称图形;实验教学;数学思维
中图分类号:G633.6? ? 文献标识码:B
文章编号:1671-489X(2020)03-0097-03
1 前言
剪中心对称图形是初中数学一种实验教学方法,而实验教学是通过学生动手操作、动脑思考开展的教学活动,目的是激发学生数学学习兴趣,提高学习质量。具体是指学生在教师的指导下,使用合适的工具剪出中心对称图形,而目前教学中常用的设计方法有两种,即以模仿为基础的理解型和以探究为基础的探索型。这两种剪中心对称图形的方法各有优点,教师可结合实际教学需要、教学时间,选择合适的方法对学生进行指导,或是将两种方法全部教给学生,在这个基础上提高中心对称图形的教学质量。
2 剪中心对称图形的两种设计方法片段记录
在教学中心对称图形时,相关的实践或是实验课程会涉及中心对称图形的裁剪问题,教师通常采用两种设计方法来剪出中心对称图形,即理解型和探索型。笔者以实践教学片段记录为素材,浅析剪中心对称图形的两种设计方法,具体内容如下。
理解型
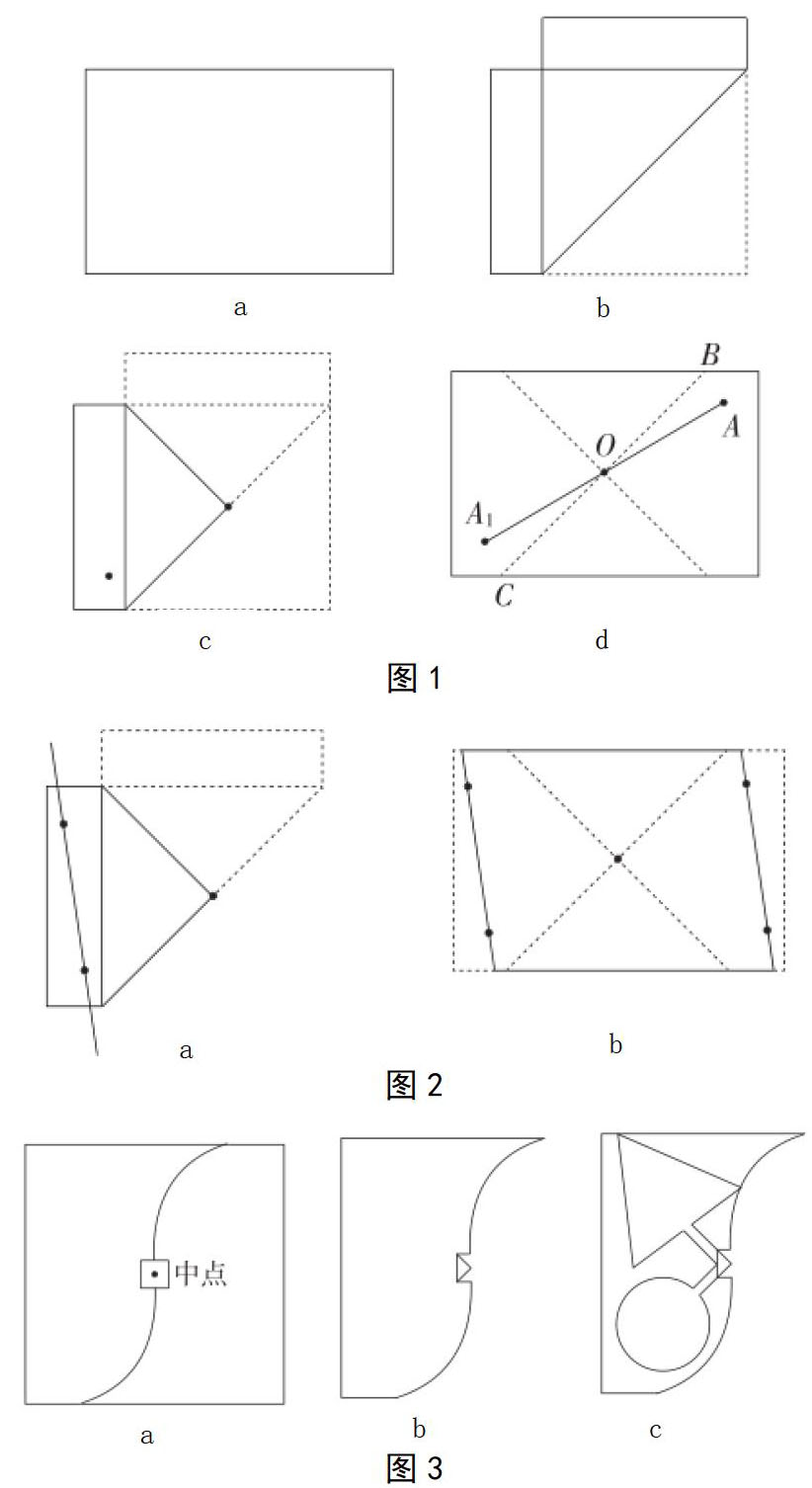
1)教师演示中心对称图形的裁剪方法,由学生来说明理由。教师按照图1的方法折叠长方形纸片,而后按照图1-c所示方法在纸片上留下一个小孔,并且将纸片展开,说明这个孔具有哪一种对称性,并且说明理由。
学生按照教师演示的方法合作完成以上步骤,且积极思考教师留下的问题。有的学生认为:两个孔为中心对称图形,这是根据折叠重合进行推理得出的结论,即线段OA与OA1相等,∠AOB与∠A1OC相等,得出∠A1OA为180°与∠AOB的和减去∠A1OC,最终结果仍为180°,进而得出点A与A1关于点O为中心对称的结论。
而后教师继续演示,并提出问题:按照图2的方法再留下一个孔,沿着两个孔连接成线,并且沿着这条线剪下,可以得到一个怎样的图形?此时学生得出结论为平行四边形。
2)学生尝试自主剪出中心对称图形。学生最为熟悉的中心对称图形就是平行四边形,教师结合这一点,要求学生开动脑筋,想一想还有哪些图案不是平行四边形,但是属于中心对称图形?学生经过多次尝试,没有总结出哪些图形仅属于中心对称图形。
3)教师指导学生按照方法剪中心对称图形。教师指导学生按照图3的方式剪一个正方形纸片,按照虚线将其剪开,沿着对角线将其进行两次对折,而后将其中的两层展开,画出对应的图形;同时将展开的图形剪下来,观察这个图形属于哪一种对称,并且说明理由。由于这个图形的操作难度较高,学生操作的时间相对较长。
学生经过操作和思考,认为该图形是中心对称图形。而后教师要求学生说明理由。学生组织语言,给出理由:中间位置的小正方形,就等于是折叠长方形纸片在其中间形成的正方形;中心的位置在折叠过程中出现四层重合,其余地方则是双层重合,而双层重合的地方剪出的图形在展开之后自然就是中心对称图形。对于学生能够总结出这样的结论并且结论合理,教师应表示鼓励,并且帮助学生了解仅为中心对称的图形。
4)理解裁剪方法后尝试设计剪中心对称图形。选择一张正方形纸片,按照前文提到的方法进行设计并且剪出中心对称图形,但该图形需要为非轴对称图形。如果课堂时间不足,这个环节可以留作课后作业,帮助学生巩固知识,使其掌握剪中心对称图形的理解型方法。
探索型
1)教师可以允许学生实施无序的尝试。教师指导学生可以尝试使用长方形纸片,利用折叠、裁剪和切开等方法得到一个非轴对称的中心对称图形。学生按照教师的指导,尝试不同的折叠、裁剪方法,而后互相交流自己的心得和想法。教师询问学生是否得到符合要求的图形,此时得到的回答是没有剪出这样的图形;继续提出疑问,引导学生分析自己得出的图形,总结困惑。大多数学生剪出的中心对称图形同时属于轴对称图形,而对称轴就是折叠线[1]。
2)利用实物探索剪中心对称图形的方法。教师准备好等宽的矩形纸片和平行四边形纸片,为便于观察,准备的矩形纸片两面颜色要有所差别。两个学生合作,分别拿着矩形和平行四边形纸片,尝试不同的方法对比两张纸片,思考如何能够一剪刀直接在矩形纸片上剪出平行四边形?在学生思考和尝试的过程中,教师需要不断巡视,发现学生很快就想到了解决办法,而后要求学生说一说自己的想法并进行演示。学生对此的描述是:将矩形纸片绕成一个
环,環的边界重合,将其与平行四边形进行对比,按照斜线的方式直接在重合的边界裁剪一刀,而后将环展开可得到平行四边形。如果班级中有学生没有完成任务,教师可以要求其他学生按照之前的演示裁剪,最终使所有学生都能够得到一个平行四边形。
在这个基础上,教师继续引导学生分析怎样折叠才能够得到平行四边形?这时学生尝试思考自己的操作与后面正确的操作之间的不同点,总结出不同颜色的面重合才有可能得到平行四边形的短边。而后教师继续追问:如何折叠才能实现不同颜色的面重合?教师还可以这个基础上带领学生探索更为优化的裁剪方法。此时学生继续思考,尝试扭转纸片,发现同样可以得到平行四边形,如图4所示。
在完成以上教学环节之后,如果课堂时间充足,教师可以允许学生自由设计,剪出中心对称图形;如果时间不允许,可以选择布置课后作业的方式巩固知识。
3 剪中心对称图形的两种设计方法之比较
两种方法的相同点
1)两种方法都需要推理、操作以及证明等环节结合。两种剪中心对称图形的设计方法都重视学生的独立思考和动手操作,在学生理性思考的同时加深他们的主观感受。在这样的学习过程中,学生能够理解数学的本质,构建理解抽象知识的基础,并且能够通过适当的直观操作掌握数学,是初中数学证明环节中不可缺少的重要步骤,是验证数学实验是否成功的关键,并且有利于培养学生的数学思维。两种设计方法都具有很强的操作性和实践性,这是数学实验非常明显的外在特点,可培养学生利用数学眼光去观察、分析问题,进而运用数学思维彻底解决问题,最终达到提高学生数学思维以及能力的教学目的。
2)两种设计方法都为学生探究数学提供了机会。剪中心对称图形是通过动态的过程来展示静态的数学知识,以直观的思维背景支持抽象的思维。在整个操作过程中,学生能够全面了解中心对称图形的性质等理论知识,感受到探索数学知识的乐趣。在剪中心对称图形两种设计方法对比教学基础上,可以达到强化学生学习效果、提升初中数学教学水平的目的[2]。
3)在完成兩种设计方法的过程中,学生都需要经历模仿以及探索的实践操作,有利于学生积累丰富的经验。经验来自社会实践,是客观事物在人们脑海中形成的印象,也是人们认识事物的一个开端。经验是人们对感官知觉的观念性总结和反思,也是人们通过内省而掌握的内容。可见,数学经验应来自数学活动。初中数学教学的目的在于培养创新型人才,而不是简单的记忆和积累。本次实验中设计的两种方法,无论是模仿还是探索,都需要一个“做”的过程。在这个过程中,学生经历推理、思考和探索等环节积累丰富的数学经验,有利于数学思维、探索能力以及解决问题能力的全面发展。相对而言,学生亲自经历探索以及寻求问题解决方法的过程,其优点远比单纯的模仿更为突出,更有利于学生获取直接的数学经验。
两种方法的不同点
1)两种方法的起点不同。
设计方法1的重点在于学生的感受,学生接受教师的指导,而后亲身体验中心对称图形的裁剪方法。教师演示剪中心对称图形的折叠和裁剪方法,学生模仿教师的操作,这是一种直观的理解,学生的体验更真实、准确。
设计方法2的重点在于中心对称图形的折叠,整个过程学生自由探索,在一次次的失败中寻找可行的方法,可培养学生的创新和探索能力。
2)裁剪过程以及每个环节需要的时间不同。
方法1的流程主要是演示、解说、模仿以及体验等,到最后则为学生应用知识,包括学生对裁剪方法原理的分析、理解和讨论等,一般需要的时间较短,多应用在结论的验证上;最后应用的环节需要时间较长,创新性不足。
方法2的流程主要是提出问题、探索答案、发现问题、再次探索等,直至发展到应用环节。这是一种探索型的学习裁剪中心对称图形的方法,虽然学生在前面几个环节需要的时间较长,但在应用环节一般耗时较短,并且作品具有显著的创新特点。
3)不同的设计方法,学生学习的难点也不同。
在设计方法1中,教师演示操作方法之后,学生很容易就掌握剪中心对称图形的步骤,相对容易总结出这样操作的理由。但由于该方法的重点在于模仿,因此,学生在最后的应用环节显得缺少创新性,创新能力不足。
而设计方法2恰好相反,因为教学的重点在于培养学生的探索能力,引导学生自主发现中心对称图形的特点,在这个基础上完成裁剪任务,能够提高学生对知识的应用能力,故而学生的应用环节发展较为顺利,学生的创新能力也得到较好的发展。其难点在于将折叠的现实问题转化为数学问题,在这个过程中缺少将现实生活转化为抽象数学问题的引导,导致学生在使用数学方法论证猜想时遇到很多困难。
总之,两种方法各有优缺点,需要教师结合学生的实际情况进行教学。
4 结语
初中数学承上启下,其教学质量直接关系着学生能否树立终身学习和运用数学的观念,影响学生后续学习数学的兴趣和积极性。为此,教师通常采用多元化的方法进行教学,激发并保持学生对数学的兴趣,提高学生数学学习和探索能力,使其能够主动学习和运用数学知识。中心对称图形是初中数学的重点内容,通过实验的方式设计两种不同的裁剪方法并对其进行对比分析,可提高学生的数学兴趣,增加学生认识数学的深度,使其在学习的同时积极应用数学。
参考文献
[1]王梅.以“三学”为导向的单元教学内容的重构:以“中心对称图形”的单元教学为例[J].初中数学教与学,2018(12):18-19.
[2]曹婕.初探信息化课堂中有效激发学生主动评价的方法:以“中心对称与中心对称图形”信息化教学设计为例[J].数学学习与研究,2018(2):116.

