数形结合思想在高中物理解题中的应用

    张郡麟

    

    

    摘 要：物理作为一门抽象性较强的学科，需加强对数形结合思想的有效应用。本文首先分析了数形结合思想的含义，然后探讨了其在高中物理解题中的具体应用，以供相关教学工作者参考。

    关键词：数形结合思想; 高中物理; 物理解题

    中图分类号：G633.7? ? ? ? ? ? ? 文献标识码：A? ?文章编号：1006-3315（2019）05-013-001

    1.数形结合思想概述

    数形结合思想主要是有效联系数与形之间的关系，在综合分析题中图形的基础上，对其中的数学表达式进行明确，从而解决物理问题。将数形结合思想应用于高中物理的解题过程中，可以进一步了解题目中包含的数量关系，从而创建合理的数学方程式，简化题目的复杂效果，提升解题速度。在物理教学中充分发挥数形结合方式的作用，可以作为一种有力的工具和方法，来解决需要解答的物理难题。物理学科中包含着大量的数学关系和物理思想，因此，为了保证一个较好的物理教学效果，可以深入渗透数形结合思想。

    2.在高中物理解题过程中，数形结合思想的具体应用

    2.1以数解形

    为了更加方便的描述物理问题，大都采用图像来表示出与问题相关的信息。图像既具有一定的优势，如形象、直觀，同时还存在着一定的缺陷，如准确性不高。在解决物理问题时，需加强对图像的分析和理解，充分挖掘出其中的有用信息，并且对图形与物理量之间的关系进行明确，通过分析其中的物理规律，来合理转换图像问题，从而实现对物理问题的有效解决。

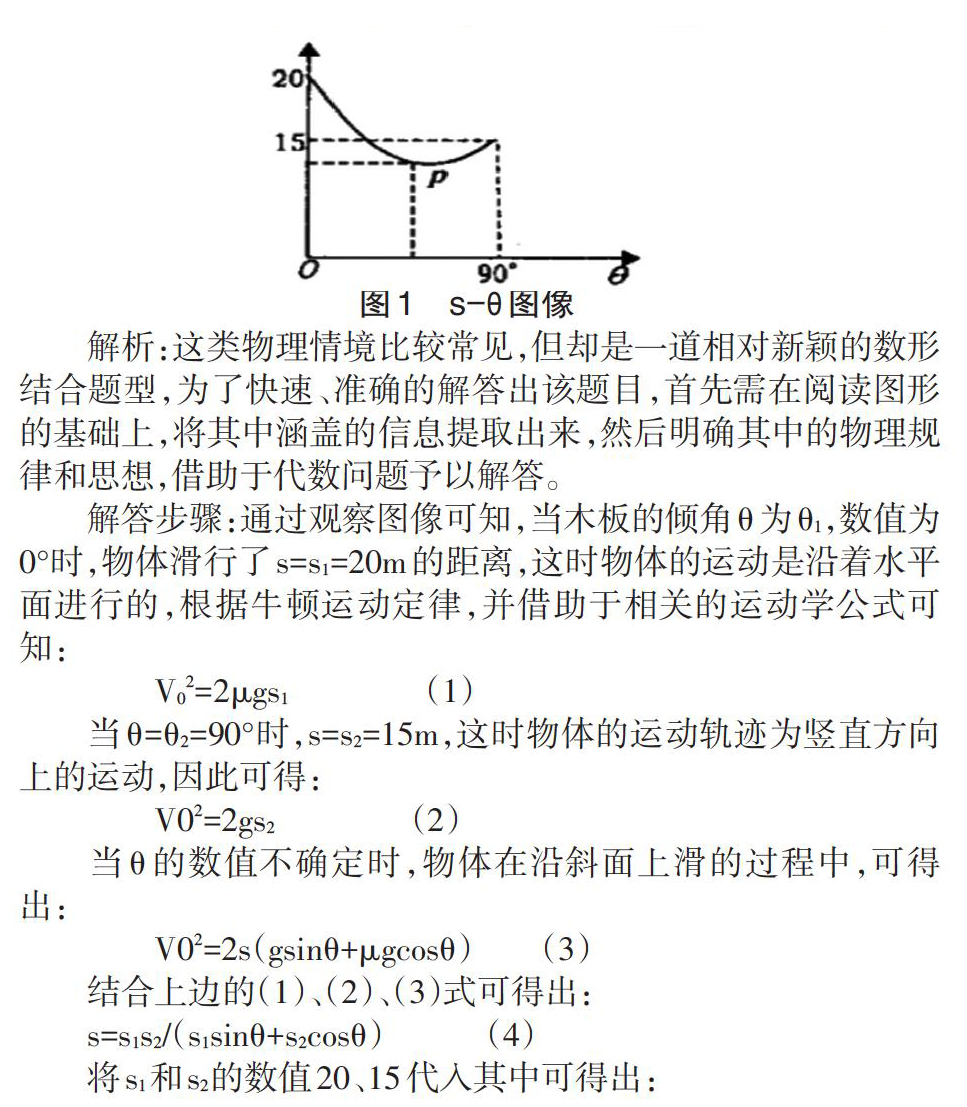
    例1，物体在沿着倾斜的木板进行滑动时，初速度为v0，并且数值的大小保持不变，根据木板倾角θ的变化，物体在上滑时，其滑动的距离s也在发生改变，如图1所示，是在大量实验的基础上，所得到的距离s与倾角θ的s-θ图像，求解出图形的最低点p的位置坐标。

    解析：这类物理情境比较常见，但却是一道相对新颖的数形结合题型，为了快速、准确的解答出该题目，首先需在阅读图形的基础上，将其中涵盖的信息提取出来，然后明确其中的物理规律和思想，借助于代数问题予以解答。

    解答步骤：通过观察图像可知，当木板的倾角θ为θ1，数值为0°时，物体滑行了s=s1=20m的距离，这时物体的运动是沿着水平面进行的，根据牛顿运动定律，并借助于相关的运动学公式可知：

    因此，为了得到距离s的最小值，θ的数值需为53°，这时s=12m，因此，图形的最低点位置p的坐标为（53°，12m）

    2.2以形助数

    以形助数即是依据图形来解决物理问题，通过仔细观察和处理图形，促使抽象的物理概念具体化，并且将其转化为形象的图形语言，从而简化问题复杂程度。有些物理问题在解决时，针对其中的已知量和未知量，很难明确它们之间的关系，为此，大都需要借助一些运动草图和受力分析图来协助分析问题，并且创建相应的关系方程予以求解;在使用代数运算的方式，难以有效解答出有些问题时，可以对其进行转化，借助图形将其解决。在解释与物理相关的概念、规律及现象时，可以使用数学语言、文字语言、物理语言进行解决。一般情况下，大都采用文字语言来阐述物理问题，为了解决问题，可将其转化为物理语言，借助于一些草图进行描述，从而简化问题的难度，促使学生明白题目中的物理量关系，并借助于方程式进行解答。

    例2，以初速度2v0从地面上向上抛出A物体，方向为竖直方向，然后再以初速度v0在相隔Δt时间之后，竖直抛出物体B，为了确保二者可以在空中相遇，Δt的数值范围是什么？

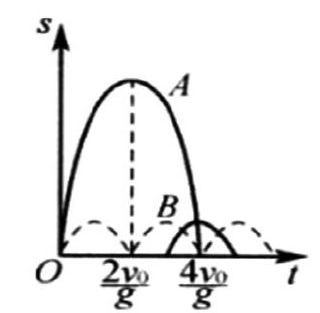
    解析：将这两个物体在竖直方向上的运动情况描绘在同一个坐标系中，如图2的s-t图像所示：

    图2物体A、B竖直运动s-t图像

    为了确保A与B相遇，需确保二者具有相同的抛出位移，即它们的图形在坐标系中需具有相交点，根据图示可知，物体B第一次与A相遇的临界条件为物体B正好落到地面;物体B抛出的最迟状态为物体B抛出的瞬间与A相遇。因此，为了确保A与B可以在空中相遇，Δt的数值范围需为：

    3.结语

    综上，在高中物理教学中，充分发挥数形结合思想的作用，具有非常重要的价值和意义，有助于简化问题的复杂性，实现对抽象问题的有效解决。因此，数形结合思想的运用，可以让学生快速了解解题的思路和方法，从而明确问题的解答方向，实现对物理问题的快速解答。为此，在实际应用过程中，教师需加强学生对这种解题方式的有效理解和掌握，强化他们对物理规律和概念的认识，从而为当前的物理教学工作提供有力指导和推动作用。

    参考文献：

    [1]刘笑岩.数形结合思想在高中物理学习中的应用体会[J]考试周刊，2018（4）：95-95